工程项目具有周期长等特点，工程质量不是旦夕之间形成的。工程建设各阶段紧密衔接，互相制约影响，所以工程建设的每阶段均对工程质量形成产生十分重要的影响。因此，工程竣工验收阶段是工程质量控制的最后一个重要环节。综上所述，工程项目质量的形成是一个系统的过程，即工程质量是由可行性研究、工程设计、工程施工和竣工验收各阶段质量的综合反映。只有有效地控制各阶段的质量，才能确保工程项目质量目标的最终实现。......
2023-11-19
水利工程建设质量控制|控制图分析结果
【摘要】：在生产过程中，按规定取样，测定其特性值，将其统计量作为一个点画在控制图上，然后连接各点成一条折线，即表示质量波动情况。（二） 控制图的绘制原材料质量基本稳定的条件下，混凝土强度主要取决于水灰比，因此可以通过控制水灰比来间接的控制强度。为说明管理图的控制方法，以设计水灰比＝0.50 为例，绘制水灰比的～R 管理图。经计算得到：图7-11控制图分析1）连续25 点无超出控制界线者。连续7 点至少有3 点接近控制界线。
前述直方图，它所表示的都是质量在某一段时间里的静止状态。但在生产工艺过程中，产品质量的形成是个动态过程。因此，控制生产工艺过程的质量状态，就成了控制工程质量的重要手段。这就必须在产品制造过程中及时了解质量随时间变化的状况，使之处于稳定状态，而不发生异常变化，这就需要利用管理图法。
管理图又称控制图，它是指以某质量特性和时间为轴，在直角坐标系所描的点，依时间为序所连成的折线，加上判定线以后，所画成的图形。管理图法是研究产品质量随着时间变化，如何对其进行动态控制的方法。它的使用可使质量控制从事后检查转变为事前控制。借助于管理图提供的质量动态数据，人们可随时了解工序质量状态，发现问题、分析原因，采取对策，使工程产品的质量处于稳定的控制状态。
控制图一般有三条线：上面的一条线为控制上限，用符号UCL 表示；中间的一条叫中心线，用符号CL 表示；下面的一条叫控制下限，用符号LCL 表示。如图7-8 所示。
在生产过程中，按规定取样，测定其特性值，将其统计量作为一个点画在控制图上，然后连接各点成一条折线，即表示质量波动情况。
应该指出，这里的控制上下限和前述的标准公差上下限是两个不同的概念，不应混淆。控制界限是概率界限，而公差界限是一个技术界限。控制界限用于判断工序是否正常。控制界限是根据生产过程处于控制状态下，所取得的数据计算出来的；而公差界限是根据工程的设计标准而事先规定好的技术要求。
（一） 控制图的种类
按照控制对象，可将双侧控制图分为计量双侧控制图和计数双侧控制图两种。
计量双侧控制图包括：平均值—极差双侧控制图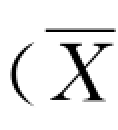 
～R 图），中位数—极差双侧控制图（X～～R 图），单值—移动极差双侧控制图（X～RS图）。
计数双侧控制图包括：不合格品数双侧控制图 （Pn图），不合格品率双侧控制图 （P图），缺陷数双侧控制图（C 图），单位缺陷数双侧控制图（u 图）。
这里我们只介绍平均值—极差双侧控制图
管理图是控制其平均值，极差R 管理图是控制其均方差。通常这两张图一起用。
（二） 控制图的绘制
原材料质量基本稳定的条件下，混凝土强度主要取决于水灰比，因此可以通过控制水灰比来间接的控制强度。为说明管理图的控制方法，以设计水灰比＝0.50 为例，绘制水灰比的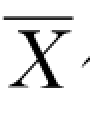
～R 管理图。
（1）收集预备数据。在生产条件基本正常的条件下，分盘取样，测定水灰比，每班取得n＝3～5 个数据 （一个数据为两次试验的平均值）作为一组，抽取的组数t ＝20～30组。如表7-3 所示。
本例收集25 组数据。
（2）计算各组平均值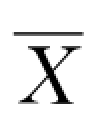
和极差R，计算结果记在右侧两栏。
（3）计算管理图的中心线，即
的平均值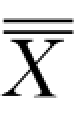
；计算R 管理图的中心线，即R 的平均值R。
图7-8 控制图
表7-3 X～R双侧控制图数据表
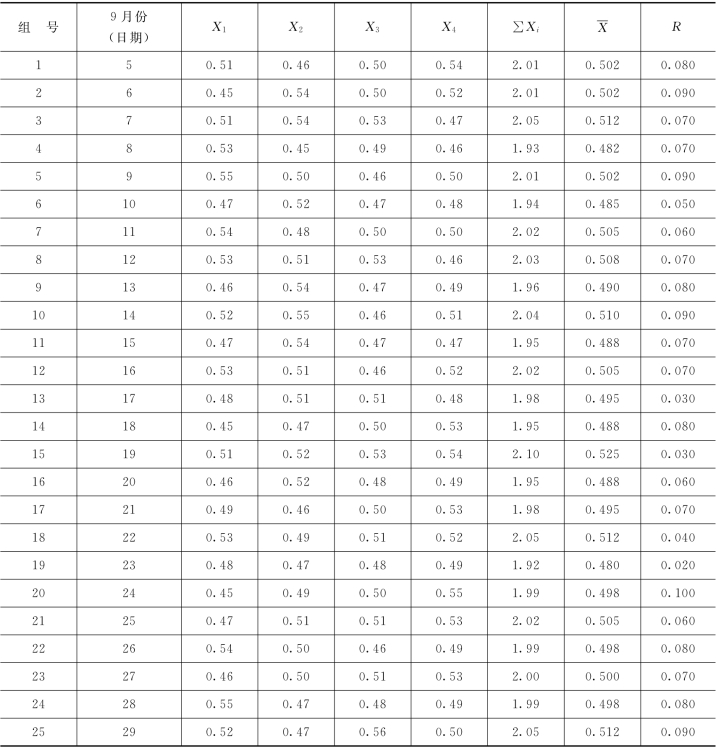
表7-4 系数A2、D3和D4随n变化的数据表
（4）计算管理界限。
式中：A2、D3、D4均为随n 变化的系数。其值如表7-4 所示。(www.chuimin.cn)
本例计算结果如下：
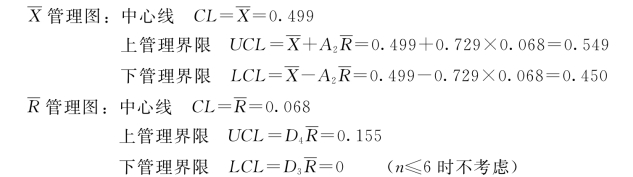
（5）画管理界限并打点，见图7-9 和图7-10。
图7-9
控制图
（三） 控制图的分析与判断
绘制控制图的主要目的是分析判断生产过程是否处于稳定状态。控制图主要通过研究点子是否超出了控制界线以及点子在图中的分布状况，以判定产品（材料）质量及生产过程是否稳定，是否出现异常现象。如果出现异常，应采取措施，使生产处于控制状态。
控制图的判定原则是：对某一具体工程而言，小概率事件在正常情况下不应该发生。换言之，如果小概率时间在一个具体工程中发生了，则可以判定出现了某种异常现象，否则就是正常的。由此可见，控制图判断的基本思想可以概括为 “概率性质的反证法”，即借用小概率事件在正常情况下不应发生的思想作出判断。这里所指的小概率事件是指概率小于1%的随机事件。
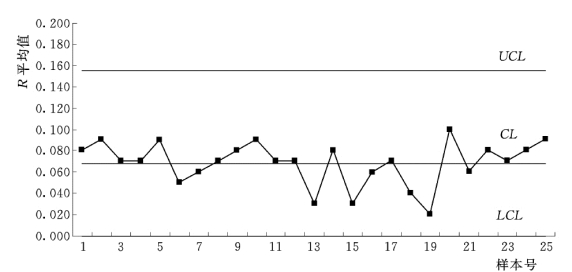
图7-10 R 控制图
主要从以下四个方面来判断生产过程是否稳定：
（1）连续的点全部或几乎全部落在控制界线内，如图7-11 （a）所示。经计算得到：
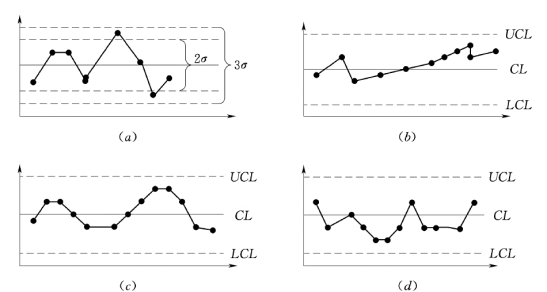
图7-11 控制图分析
1）连续25 点无超出控制界线者。
2）连续35 点中最多有一点在界外者。
3）连续100 点中至多允许有2 点在界外者。
这三种情况均为正常。
（2）点在中心线附近居多，即接近上、下控制界线的点不能过多。接近控制界线是指点子落在了μ±2σ以外和μ±3σ以内。如属下列情况判定为异常：连续3 点至少有2 点接近控制界线。连续7 点至少有3 点接近控制界线。连续10 点至少有4 点接近控制界线。
（3）点在控制界线内的排列应无规律。以下情况为异常：
1）连续7 点及其以上呈上升或下降趋势者，如图7-11 （b）所示。
2）连续7 点及其以上在中心线两侧呈交替性排列者。
3）点的排列呈周期性者，如图7-11 （c）所示。
（4）点在中心线两侧的概率不能过分悬殊，如图7-11 （d）所示。以下情况为异常：连续11 点中有10 点在同侧；连续14 点中有12 点在同侧；连续17 点中有14 点在同侧；连续20 点中有16 点在同侧。
有关水利工程建设质量控制的文章
- 详细阅读
-
水利工程建设质量控制标准详细阅读
但水利水电工程中厂房道路生活设施等工程应参照国家和其他行业的质量检验评定标准进行评定。至此，水利水电建设工程施工质量的质量检验和评定标准的法规体系已基本形成，为加强水利水电工程施工质量管理，搞好工程质量控制，提高工程质量奠定了良好的基础。......
2023-11-19
-
水利工程建设质量控制：因果分析图法详细阅读
（一） 因果分析图概念因果分析图法是利用因果分析图来系统整理分析某个质量问题（结果）与其产生原因之间关系的有效工具，因果分析图也称特性要因图，又因其形状常被称为树枝图或鱼刺图。因果分析图基本形式如图7-14 所示。（二） 因果分析图绘制下面结合实例加以说明。因果分析图的绘制步骤与图中箭头方向恰恰相反，是从“结果”开始将原因逐层分解的，具体步骤如下：明确质量问题—结果。图7-15 是混凝土强度不足的因果分析图。......
2023-11-19
-
水利工程建设质量控制：成因分析方法详细阅读
要分析究竟是哪种原因所引起，必须对质量问题的特征表现，以及其在施工中和使用中所处的实际情况和条件进行具体分析。分析方法很多，但其基本步骤和要领可概括如下。分析、比较和判断，找出最可能造成质量问题的原因。（二） 分析要领分析要领的方法是逻辑推理法，其基本原理是：确定质量问题的初始点，即所谓原点，它是一系列独立原因集合起来形成的爆发点。因其反映出质量问题的直接原因，而在分析过程中具有关键性作用。......
2023-11-19
-
水利工程建设质量事故分析详细阅读
造成工程质量事故的原因多种多样，但从整体上考虑，一般原因大致可以归纳为下列几方面。违反基本建设程序而直接造成工程质量事故的问题有：可行性研究不充分。致使该工程推迟一年多发电，花费质量事故处理费用上亿元。（五） 建筑材料及制品不合格不合格工程材料、半成品、构配件或建筑制品的使用，必然导致质量事故或留下质量隐患。......
2023-11-19
-
水利工程建设质量控制：合同内外质量检验详细阅读
（一） 合同内质量检验合同内检验是指合同文件中作出明确规定的质量检验，包括工序、材料、设备、成品等的检验。若重新检验结果证明这些材料和工程设备不符合合同要求，则应由承包人承担重新检验的费用和工期延误责任；若重新检验结果证明这些材料和工程设备符合合同要求，则应由发包人承担重新检验的费用和工期延误责任。......
2023-11-19
-
水利工程建设质量控制：质量认证基本概念详细阅读
质量认证是由可以充分信任的第三方证实某一经鉴定的产品或服务符合特定标准或规范性文件的活动。依据标准中的性能要求进行认证叫做合格认证；依据标准中的安全要求进行认证叫做安全认证，前者是自愿的，后者是强制性的。质量管理体系具有下列特征：图9-1认证标志合格认证标志图；安全认证标志图；长城标志图；PRC标志图认证的对象是质量体系而不是产品。......
2023-11-19
-
水利工程建设质量控制方案详细阅读
（一） 合同项目质量控制程序监理机构应在施工合同约定的期限内，经发包人同意后向承包人发出进场通知，要求承包人按约定及时调遣人员和施工设备、材料进场进行施工准备。监理机构应协助发包人向承包人移交施工合同约定应由发包人提供的施工用地、道路、测量基准点以及供水、供电、通信设施等开工的必要条件。由此增加的费用和工期延误造成的损失由发包人承担。......
2023-11-19
相关推荐