水利工程建设质量数据分布规律

2023-11-19 理论教育版权反馈

【摘要】：质量数据的集中趋势和离散趋势反映了总体（样本）质量变化的内在规律性。质量数据具有个体数值的波动性和总体（样本）分布的规律性。一般来说，计量连续的数据是属于正态分布。正态分布规律是各种频率分布中用得最广的一种，在水利工程施工质量管理中，量测误差、土质含水量、填土干密度、混凝土坍落度、混凝土强度等质量数据的频数分布一般认为服从正态分布。

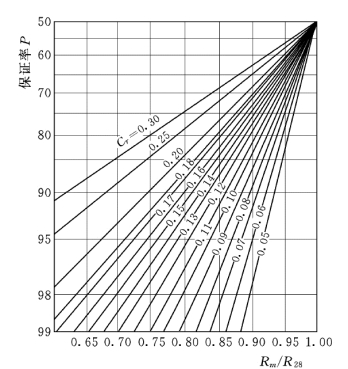
pagenumber_ebook=121,pagenumber_book=113

图7-2　混凝土强度保证率曲线

在实际质量检测中，我们发现即使在生产过程是稳定正常的情况下，同一总体（样本）的个体产品的质量特性值也是互不相同的。这种个体间表现形式上的差异性，反映在质量数据上即为个体数值的波动性、随机性，然而当运用统计方法对这些大量丰富的个体质量数值进行加工、整理和分析后。我们又会发现这些产品质量特性值（以计量值数据为例）大多都分布在数值变动范围的中部区域，即有向分布中心靠拢的倾向，表现为数值的集中趋势；还有一部分质量特性值在中心的两侧分布，随着逐渐远离中心，数值的个数变少，表现为数值的离散趋势。质量数据的集中趋势和离散趋势反映了总体（样本）质量变化的内在规律性。质量数据具有个体数值的波动性和总体（样本）分布的规律性。

（一）质量数据波动的原因

在生产实践中，常可看到设备、原材料、工艺及操作人员相同的条件下，生产的同一种产品的质量不同，反映在质量数据上，即具有波动性，亦称为变异性。究其波动的原因，有来自生产过程和检测过程的，但不管哪一个过程的原因，均可归纳为下列五个方面因素的变化：

（1）人的状况，如精神、技术、身体和质量意识等。

（2）机械设备、工具等的精度及维护保养状况。

（3）材料的成分、性能。

（4）方法、工艺、测试方法等。

（5）环境，如温度和湿度等。

根据造成质量波动的原因，以及对工程质量的影响程度和消除的可能性，将质量数据的波动分为两大类，即正常波动和异常波动。质量特性值的变化在质量标准允许范围内波动称之为正常波动，是由偶然因素引起的；若是超越了质量标准允许范围的波动则称之为异常波动，是由系统性因素引起的。

1.偶然性因素(www.chuimin.cn)

它是由偶然性、不可避免的因素造成的。影响因素的微小变化具有随机发生的特点，是不可避免、难以测量和控制的，或者是在经济上不值得消除，或者难以从技术上消除。如原材料中的微小差异、设备正常磨损或轻微振动、检验误差等。它们大量存在但对质量的影响很小，属于允许偏差、允许位移范畴，引起的是正常波动，一般不会因此造成废品，生产过程正常稳定。通常把4M1E因素的这类微小变化归为影响质量的偶然性原因、不可避免原因或正常原因。

2.系统性因素

当影响质量的4M1E因素发生了较大变化，如工人未遵守操作规程、机械设备发生故障或过度磨损、原材料质量规格有显著差异等情况发生时，没有及时排除，生产过程在不正常，产品质量数据就会离散过大或与质量标准有较大偏离，表现为异常波动，次品、废品产生。这就是产生质量问题的系统性原因或异常原因。由于异常波动特征明显，容易识别和避免，特别是对质量的负面影响不可忽视，生产中应该随时监控，及时识别和处理。

（二）质量数据分布的规律性

上面已述及，在正常生产条件下，质量数据仍具有波动性，即变异性。概率数理统计在对大量统计数据研究中，归纳总结出许多分布类型。一般来说，计量连续的数据是属于正态分布。计件值数据服从二项分布，计点值数据服从泊松分布。正态分布规律是各种频率分布中用得最广的一种，在水利工程施工质量管理中，量测误差、土质含水量、填土干密度、混凝土坍落度、混凝土强度等质量数据的频数分布一般认为服从正态分布。正态分布概率密度曲线如图7-3 所示。从图中可知：

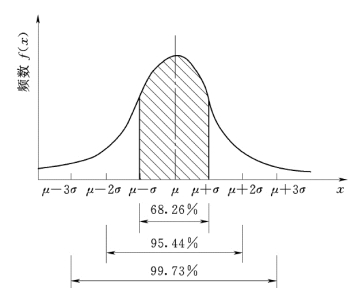
pagenumber_ebook=123,pagenumber_book=115

图7-3　正态分布曲线

（1）分布曲线关于均值μ是对称的。

（2）标准差σ大小表达曲线宽窄的程度，σ越大，曲线越宽，数据越分散；σ越小，曲线越窄，数据越集中。

（3）由概率论中的概率和正态分布的概念，查正态分布表可算出：曲线与横坐标轴所围成的面积为1；正态分布总体样本落在（μ－σ，μ＋σ）区间的概率为68.3%；落在（μ－2σ，μ＋2σ）区间的概率为95.4%，落在（μ－3σ，μ＋3σ）区间的概率为99.7%。也就是说，在测试1000 件产品质量特性值中，就可能有997 件以上的产品质量特性值落在区间（μ－3σ，μ＋3σ）内，而出现在这个区间以外的只有不足3 件。这在质量控制中称为“千分之三”原则或者“3σ原则”。这个原则是在统计管理中作任何控制时的理论根据，也是国际上公认的统计原则。

水利工程建设质量数据分布规律

相关推荐