光矢量变换色矢量复频谱色度理论解析及反射光显色衰减机制探究

2023-11-18 理论教育版权反馈

【摘要】：这就是一部分光量在墨层内被颜料颗粒吸收，另一部分光量由于反复、多次散射最终以热的方式消耗在墨层内，这两部分合称为衰减光。设总的反射光为Iρ，那么图9-14反射光路径图显然，当墨层总厚度b一定时，颜料颗粒平均直径d越小，微层数n就越大。任何事物总是有利也有弊，油墨层的中上层的反射光对总反射光的贡献是主要的。

世间万物，林林总总，物体颜色五彩缤纷。这些物体的颜色绝大多数都属于反射光显色。白光照射在物体上，一部分从表面反射出来，一部分入射到物体表层内部不同部位的一定深度，被物体吸收或散射而衰减，剩余的再反射出来。由于物体表面层分子结构及颗粒形状、大小不同，入射光在表层内不同深度处的路径及方向是随机散开的。从表层内部不同深度处再反射出来的光与表面上的反射光一同构成物体反射光。这些光就决定了物体的外观颜色。足见物体反射光的路径比透射光要复杂得多。

除了物体自身的条件显示颜色以外，人们为了一定目的及需要，往往使用色料涂饰的方法使物体显示颜色。这些色料有装饰用的涂料、油漆，有印染用的色浆，有印刷油墨等。其中以印刷油墨显色机理较为复杂。不仅不同油墨本身显示不同颜色，更多的是两种不同颜色油墨调和或叠印改变显示出新的颜色。下面就以油墨为例作进一步讨论。

印刷油墨的主要成分是树脂一类连结料和颜料。连结料是天然的或是人工合成的高分子化合物，是透明的连续介质。而颜料却是以颗粒状分散在连结料中，形成一个悬浮状多相体系。颜料颗粒不仅形状不一，大小也不一致，对入射光不但有选择性吸收，它的颗粒表面对光线还有散射和绕射作用。可见从光路上来说，印刷油墨远不是那种理想的光学介质。光线进入墨层以后，颜料颗粒表面在经过光散射、绕射作用下，完全改变了最初的入射方向。不管从哪个方向入射到颜料层内颗粒表面的光线，一部分被颜料颗粒选择性吸收，剩余的再以随机的方向散射出去。这些光再入射到邻近的颜料颗粒上，照样又是被吸收和再散射，依次类推。因此墨层内这些光的路径及方向是随机散布的。虽然如此，最终的结果是确定的。这就是一部分光量在墨层内被颜料颗粒吸收，另一部分光量由于反复、多次散射最终以热的方式消耗在墨层内，这两部分合称为衰减光。更多的光量入射到墨层内不同深度处再反射出来。关于反射光又分为几种情况，首先是并未进入墨层，由表面直接反射出来，其次才是从墨层内部不同深度处反射出来。不管光的路径多么复杂，归纳起来可以把它分成向下的、水平的和向上的三个方向，其反射光路径如图9-14所示。

设颜料颗粒的平均直径为d，相当于每个微层的厚度，如果墨层厚度为b，那么它是由n个微层叠加而成，nd=b。

设初始入射光为I0，首先在墨层表面上有反射光I0ρ，这里ρ为反射率。每个微层的透射率为τ，τ恒小于1。入射光进入墨层以后，在每一个微层内既有衰减光ai，也有透射光τi，这里的i表示微层数，还有反射光I0τ2iρ。但是最终透射光还是以反射光的方式从墨层内不同深度处再反射出来。这样墨层就没有透射光了。从图9-14看，初始的入射光及透射光是向下方向，衰减光是水平方向，反射光是向上方向。设总的反射光为Iρ，那么

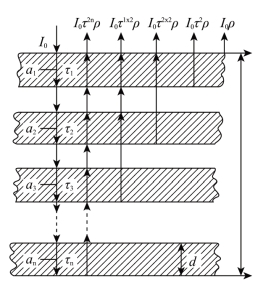
pagenumber_ebook=103,pagenumber_book=96

图9-14　反射光路径图(www.chuimin.cn)

pagenumber_ebook=103,pagenumber_book=96

显然，当墨层总厚度b一定时，颜料颗粒平均直径d越小，微层数n就越大。当n很大时，τ2n连乘的积可能趋于零。由此我们知道，虽然总的反射光Ip是由I0ρ与指数为n个反射光因子项相加而成的，但是不同n的因子项在加和总量中的权重是不同的。墨层越往上n值越小，权重因子数值越大，对总的反射光的贡献也越大。反之，n值越大，对反射光的贡献就越小。

在图9-14中，每个微层内还有水平方向箭头代表的衰减光ai，它又包含两部分，主要部分是颜料颗粒对入射光选择性吸收；另一部分是颜料颗粒不规则表面对入射光的散射作用，最终以热的方式消耗在微层内。其中颜料颗粒对入射光选择性吸收是油墨产生色彩的主要原因。墨层的颜料颗粒平均直径越小，微层数也越多，选择性吸收的光也越多，油墨的色彩越鲜艳，饱和度也越高。反映在复频谱色度图上，在选择性吸收频域，反射率是低的。那么这个方向低了，白光中色矢量失去平衡，在它的反方向产生的色彩强度就高了。这正是我们希望的。

任何事物总是有利也有弊，油墨层的中上层的反射光对总反射光的贡献是主要的。但是也因为中上层反射光路径短，不能充分被吸收，加之表面反射光还是白光，致使总反射光的成分里彩色光的比重偏低，这就是为什么一般说反射光的色彩饱和度总比透射光要低。

通过以上讨论，可以总结以下几点：

光矢量变换色矢量复频谱色度理论解析及反射光显色衰减机制探究

相关推荐