由此可以设想，可见光的频率从红端的384MMHz开始，在复频谱上按逆时针方向逐渐增加到紫端的768MMHz时，那些中间频率的相位从初始0相位逐渐增加到2π。在复频谱极坐标上，0、2π、4π等都是0相位，在可见光所有频率的相位仅仅分布在一个2π条件下，频率因子n就不能是正整数。可见光频率、波长与相位对应关系见书后附表。频率v与相位θ不仅成正比关系，而且呈环状均匀分布。......
2023-11-18
光矢量变换色矢量复频谱色度理论解析：合成效率的影响因素
【摘要】：现在让合成效率ηc来回答这个问题。虽然合成效率很高，由于r1与r2相差过于悬殊，合成的中间色基本上还是趋同于r2的颜色，意义不大。从实用价值方面考虑，当r1=r2时，合成效率ηc会怎样？（8-6）式告诉我们，在两色矢量的模相同的情况下，提高合成效率的最好途径是使两色矢量r1与r2之间夹角φ变小，φ越小，合成效率越高。
用色矢量合成的方法产生一个新的颜色，人们总是希望这个新的中间色颜色越鲜艳越好。可是（8-3）式告诉我们，两个色矢量之间的夹角φ越大，平衡效率ηba也变大，平衡效率增大，意味着在合成产生新的中间色的同时，另外还产生平衡的白色，从而使颜色的饱和度趋向降低。如何提高合成中间色的饱和度向我们提出一个新的要求。现在让合成效率ηc来回答这个问题。
合成效率ηc由合成后产生的色矢量rp的模与两个色矢量r1与r2模之和的比表示，由图8-1可知：
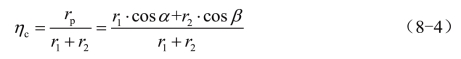
（8-4）式告诉我们，合成效率ηc既与r1、r2模的大小有关，由于α=φ-β，也与两色矢量之间夹角φ的大小有关。当r2>>r1时，r1·cos α的影响变小，这时
从图7-6可以看到：r2变大，则β变小，ηc则趋于1。虽然合成效率很高，由于r1与r2相差过于悬殊，合成的中间色基本上还是趋同于r2的颜色，意义不大。从实用价值方面考虑，当r1=r2时，合成效率ηc会怎样？这时α=β=
，那么
而（8-3）式平衡效率ηba在r1=r2情况下
，则显然有
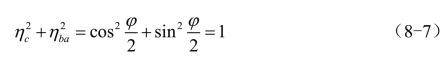(www.chuimin.cn)
也就是说，在两个色矢量的模相等的情况下，当两色矢量夹角φ=0°时，ηba=0，则ηc=1，反之，当φ=180°时，ηba=1，ηc=0。在一般条件下，0°<φ<180°，ηc与ηba此消彼长，但是无论怎样变化，二者各个平方之和总是等于1，这就是（8-7）式的结论。（8-6）式告诉我们，在两色矢量的模相同的情况下，提高合成效率的最好途径是使两色矢量r1与r2之间夹角φ变小，φ越小，合成效率越高。
色矢量的特点是它既有模的数值大小的变化，又有方向（相位）的不同，因而两矢量相加的结果就不像纯数值相加那样简单。从几何学来说，它遵循平行四边形原理，从色度学上来说，它遵循中间色定律。我们看到格拉斯曼有关中间色定律是这样说的：“任何两个非补色相混合，便产生中间色，其色相决定于两个颜色的相对数量，其饱和度决定于二者在色相顺序上的远近。”
由于r1·sin α=r2·sin β，r1变小，则α变大，反之，r2变大，则β变小。因而人们把合成中间色定律称“杠杆定律”。
如果说格拉斯曼的中间色定律依靠的是人的视觉对颜色混合规律给出的是一个定性描述的话，那么复频谱色度给出的平衡效率与合成效率则是给中间色定律一个定量描述。你看，它的原话说：“任何两个非补色相混合”，这里并没有给“补色”一个界定。可是在复频谱色度里，任何一个彩色都存在一个色矢量，若两个颜色混合，两个色矢量的夹角φ必须小于180°，这样一对颜色才能称非补色。原话说：“便产生中间色”，在复频谱色度上，两个色矢量相加以后便产生一个新的色矢量，这个新的色矢量就是平行四边形中间的对角线，见图8-1。“其色相决定于两个颜色的相对数量。”这里所说颜色相对数量，实际上是指两个色矢量模的相对比值，也就是r2/r1的比值n。从图8-1可以看到，若r1变大，sin α就变小，中间色的位置就靠近r1；反之若r2变大，sin β就变小，中间色的位置就靠近r2。原话说：“其饱和度决定于二者在色相顺序上的远近。”前面平衡效率讨论中指出，只要两个色矢量r1与r2夹角φ>0°，那么它们合成在产生新的中间色rp的同时，在rp的垂直方向还产生一对大小相等方向相反的色矢量h1与h2，见图8-1，这一对色矢量平衡以后转变成白色，与新产生的彩色rp2混合在一起，从而降低了新颜色的饱和度。而平衡效率就给出了平衡白色量的相对值。两色矢量色相顺序越远，色相夹角φ就越大，平衡效率ηba就越高，饱和度降低的也就越多。
若两个色矢量r1与r2合成后产生一个新的中间色矢量rp，它们三者间的关系应遵照余弦定理：当两个色矢量的夹角为φ时，中间色矢量的模rp为
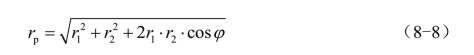
若已知两个色矢量r1和r2及夹角φ的值，就可以利用（8-8）式计算出合成色矢量rp的值。
有关光矢量变换色矢量复频谱色度理论解析的文章
- 详细阅读
-
光矢量变换色矢量复频谱色度理论解析-平衡效率详细阅读
当色矢量r1与r2合成rp时产生h1和h2两个平衡矢量如图8-1所示。可以看到平衡色矢量模的大小既与r1与r2模的大小有关，也与φ及α与β大小有关。假若r2=r1，n=1，α=，这时也就是说只有在r2=r1与α=β=的条件下，才有最大的平衡效率ηba。（8-3）式表明若r1与r2为一对互补色矢量，并且φ=180°时，ηba=1，两色矢量完全平衡，转化为中性色。......
2023-11-18
-
光矢量变换色矢量复频谱解析详细阅读
在两级积分变换里，设定一个时间T，于是原本在时域t里光的动态频率v映射在复频谱上变成了复频域静态θ的相位。式Z=reiθ就是光色变换复频谱数学模型的表达式。拉普拉斯变换只是复数平面，Z变换则将复数平面进一步变换为周期循环的相平面。......
2023-11-18
-
光矢量变换色矢量复频谱色度理论解析结果详细阅读
复频谱色度计算不需要把可见光分成红、绿、蓝三个原色，它只需要一台分光光度计把每一个频率相对功率分布或反（透）射率以矢端函数曲线的形式记录下来。可见光全频域由无限多个微色矢量端点连续绘出矢端函数曲线，形成一个色矢量系统，有了矢端函数曲线就可以计算出复频谱颜色特征数值。一般说矢端函数曲线在复频谱上包围的面积越大，它被平衡的色矢量强度也越大，白色越多，亮度也越高。......
2023-11-18
-
光矢量变换与复频谱色度理论解析详细阅读
不同色光相加不是在能量层级上相加，在复频谱上是它们的色矢量相加。人眼虽然看不见色矢量，我们可以把一个准单色光的能量、微弧度及色矢量映射在复频谱图上。虽然微弧度Δθ很窄，可是它里面众多的色矢量分别处在以r为中心均等对称的相位上，这些色矢量在自发地合成中心色矢量r时，在色矢量r的垂直方向又合成出两个大小相等但是方向相反的分色矢量。很显然，这些分色矢量会自发地互相平衡。......
2023-11-18
-
近代颜色科学的兴起-光矢量变换色矢量复频谱色详细阅读
十七世纪英国天才科学家牛顿总结亲历的实验，为近代颜色科学做出了开创性的贡献。图3-1牛顿颜色环十九世纪初，英国年轻科学家杨以杨氏光干涉实验力挺光的波动说，反对牛顿的微粒说。说到颜色科学家，不能不提到格拉斯曼，他在1854年提出颜色变化的三条定律。在色彩学上称“同色异谱”。科学技术要求对颜色变化的规律给出定量的描述。......
2023-11-18
-
常用印刷油墨复频谱色度图及光矢量变换色矢量复详细阅读
下面列出了12种油墨的复频谱颜色特征数值，如表9-1所示，绘制出该12种油墨的复频谱色度图，如图9-1到图9-12所示。以图9-2桃红油墨为例，复频谱色相值为25.3921°，它的矢端函数曲线包围的面积大部分在红色区域。复频谱色相与光的频率、波长相对应，而在CIELab色度系统中，其色相值没有上述对应关系。更为重要的是，如图9-7所示，中黄油墨的复频谱饱和度为39.5378，而CIE-Lab的饱和度高达109.8755。......
2023-11-18
-
光矢量变换色矢量复频谱色度理论解析-同色异谱详细阅读
同色异谱这一命题表明色与谱二者之间确实存在着微妙的关系。“同色”指两个物体的颜色完全相同；“异谱”则是两个相同颜色的辐亮度光谱结构却不同。但是电视上的绿色是由荧光屏上红、绿、蓝三基色加和产生的，这里三基色的光谱结构与树叶中叶绿素分子的光谱结构肯定不同，也就是说这二者是同色却是异谱。人们只需做到是同色，不必刻意追求同谱。解释同色异谱的奥秘就在于复频谱里的色矢量。......
2023-11-18
相关推荐