大红的外套大衣可与黑色长裤长裙搭配，但上衣仍以白色为理想。浅黄色上衣可与咖啡色裙子，裤子搭配，也可以在浅黄色的衣服上接上浅咖啡色的蕾丝花边，使衣服的轮廓更为明显。注意，蓝色与绿色虽然同是寒色，但是切勿将深蓝与深绿互相搭配，即使浅绿也不适宜，所以蓝色的牛仔裤若与绿色上衣相配，就会非常难看。......
2023-08-04
合成不同主波长目标色的方法
【摘要】：下面将以色相由低至高的顺序在每个色域里选三个主波长作为目标色，用三刺激值里色矢量相加的方法给出目标色的主波长。以该直线rp为对角线，以色矢量rr和rg为两边，作平行四边形，那么rr与rg即合成目标色的两个色矢量。色矢量rr与rg合成主波长为610nm目标色p的示意图如图7-2所示。图7-5色矢量rg与rb合成主波长为480nm目标色的示意图已知三刺激值两色矢量夹角φ=130.259 °，α=70.873 °，β=59.386 °，sin φ=0.763131，cos φ=-0.646244，tg α=2.88343。
三基色RGB将复频谱分成三个色域：RG色域、GB色域和BR色域，如图6-2所示。下面将以色相由低至高的顺序在每个色域里选三个主波长作为目标色，用三刺激值里色矢量相加的方法给出目标色的主波长。
例1.设目标色主波长为680nm。求解合成该目标色的两个色矢量的模各是多少。
解：
第一步，由已知波长λ换算出复频谱色相H，设光速c=299792nm×1012·s-1，λ=680nm，则色相
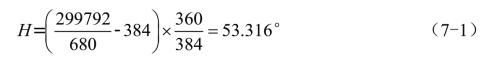
显然，它位于RG色域，应该用R色矢量rr与G色矢量rg相加合成（以下文字中色矢量的模均简称色矢量）。
第二步，在复频谱上作色矢量rr和rg合成主波长为680nm的目标色示意图，如图7-1所示。从原点作53.316°方向直线，指向目标色色相方向。以该直线rp为对角线，以色矢量rr和rg为两边，作平行四边形，那么rr与rg即合成目标色的两个色矢量。
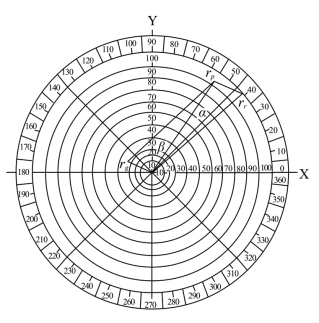
图7-1 色矢量 rr和rg合成主波长为680nm目标色示意图
第三步，查该目标色波长处V（λ）=0.017，三刺激值分别为
（λ）=0.01687，
（λ）=0.00003，由此它们的辐亮度分别为：
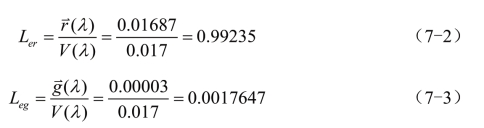
已知三基色矢量rr与rg的夹角φ=113.151°，那么rp与rr的夹角α=11.809°，rp与rg的夹角β=101.342°，如图7-1所示，于是sin φ=0.919472，cos φ=-0.393156，tg α=0.29075。
按照正弦定理，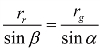
，rr·sin α=rg·sin β，而β=φ-α，所以sin β=sin （φ-α）=sin φ cos α–cos φ sin α，代入上式，得
rr·sin α=rg·（sin φ cos α–cos φ sin α）=rg·sin φ cos α–rg·cos φ sin α，方程两边同除以cos α，得rr·tg α=rg·sin φ-rg·cos φ tg α，那么
利用（6-2）式，它们的微窄波长域：Δλr=1.99nm，Δλg=0.05nm。
若预先设定Δλr=1.99nm，通过计算得到R的色矢量rr=9.962，G的色矢量rg=2.0793，由它俩合成的目标色rp的色相Hp=53.316°，对应波长为680nm。
例2.设目标色主波长为610nm。求解合成该目标色的两个色矢量模各是多少。
解：参照例1解题步骤，不过，文字叙述从简，以下各题都照此例从简。目标色在复频谱上的色相为H=100.746°，位于RG色域，应该用R色矢量rr和G色矢量rg相加合成。色矢量rr与rg合成主波长为610nm目标色p的示意图如图7-2所示。
图7-2 色矢量rr与rg合成主波长为610nm目标色的示意图
已知两色矢量夹角φ=113.151°，α=59.239°，β=53.912°，sin φ=0.919472，cos φ=-0.393156，tg α=1.68115。三刺激值
，V（λ）=0.503，那么
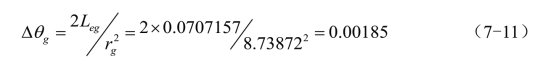
利用（6-2）式，有Δλr=1.99nm，Δλg=0.113nm。
若预先设定Δλr=1.99nm，通过计算得到R的色矢量rr=8.2181，G的色矢量rg=8.73872，由它们俩合成的目标色矢量rp的色相Hp=100.746°，对应波长为610nm。
例3.设目标色主波长为550nm。求解合成该目标色的两个色矢量的模各是多少。
解：目标色在复频谱上的色相Hp=151.009°，位于RG色域，应该用R色矢量rr和G色矢量rg相加合成。色矢量rr与rg合成主波长为550nm目标色rp的示意图如图7-3所示。
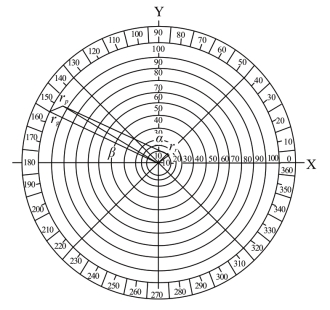
图7-3 色矢量rr与rg合成主波长为550nm目标色的示意图
已知两色矢量夹角φ=113.151°，α=109.502°，β=3.649°，sin φ=0.919472，cos φ=-0.393156，tg α=-2.82360。三刺激值
，V（λ）=0.995，
那么，按照上述两例题计算步骤与方法：
Ler=0.022905，Leg=0.212844，假定Δθr=0.01，那么rr=2.14032，由此，rg=31.7002，Δθg=0.00424。则有：Δλr=1nm，Δλr=0.26nm。
若设定Δλr=1nm，通过计算得到R的色矢量rr=2.14032，G的色矢量rg=31.7002，由它俩合成目标色的色矢量rp的色相Hp=151.009°，波长为550nm。
例4.设目标色主波长为530nm。求解合成该目标色的两个色矢量的模各是多少。
解：目标色在复频谱上的色相Hp=170.292°，位于GB色域，应该用G的色矢量rg和B的色矢量rb相加合成。色矢量rg与rb合成主波长为530nm目标色的示意图如图7-4所示。
图7-4 色矢量rg与rb合成主波长为530nm目标色的示意图
已知两色矢量夹角φ=130.26°，α=15.6344°，β=114.625°，tg α=0.279845，sin φ=0.763131，cos φ=-0.646244，三刺激值
V（λ）=0.862，那么：
Leg=0.235696，Leb=0.0063691；假定Δθg=0.002，于是：rg=15.3524，rb=4.55126， 由此，Δθb=0.000615。则有：Δλg=0.12nm，Δλb=0.025nm。
若设定Δλg=0.12nm，通过计算得到G的色矢量rg=15.3524，B的色矢量rb=4.55126，由它俩合成目标色P的色矢量rp的色相Hp=170.292°，对应波长为530nm。
例5.设目标色主波长为480nm，求解合成该目标色的两个色矢量的模各是多少。(www.chuimin.cn)
解：目标色在复频谱上的色相Hp=225.531°，位于GB色域，应该用G的色矢量rg和B的色矢量rb相加合成。色矢量rg与rb合成主波长为480nm目标色的示意图如图7-5所示。
图7-5 色矢量rg与rb合成主波长为480nm目标色的示意图
已知三刺激值
两色矢量夹角φ=130.259 °，α=70.873 °，β=59.386 °，sin φ=0.763131，cos φ=-0.646244，tg α=2.88343。那么：
Leg=0.281583，Leb=1.04273，假定Δθg=0.0075，于是：rg=8.66538，rb=9.5131，则Δθb=0.023，Δλg=0.456nm，Δλb=0.892nm。
若设定Δλg=0.456nm，通过计算得到G的色矢量rg=8.66538，B的色矢量rb=9.5131，由它俩合成的目标色rp的色相Hp=225.531°，位于GB色域，波长为480nm。
例6.设目标色主波长为440nm，求解合成该目标色的两个色矢量的模各是多少。
解：目标色在复频谱上的色相Hp=278.76°，位于GB色域，应该用G的色矢量rg和B的色矢量rb相加合成。色矢量rg与rb合成主波长为440nm目标色的示意图如图7-6所示。
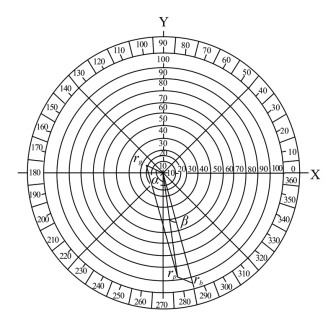
图7-6 色矢量rg与rb合成主波长为440nm目标色的示意图
已知两色矢量夹角φ=130.259°，α=124.103°，β=6.156°，sin φ=0.763131，cos φ=-0.646244，tg α=-1.47683。三刺激值：
=0.31228，V（λ）=0.023。假定Δθg=0.008，那么：
Leg=0.0647826，Leb=13.5774，则：rg=4.02438，rb=30.8583，由此，Δθb=0.031，那么Δλg=0.486nm，Δλb=1.2nm。
若设定Δλg=0.486nm，通过计算得到G的色矢量rg=4.02438，B的色矢量rb=30.8583，由它俩合成的目标色rp的色相Hp=278.76°，波长为440nm。
例7.设目标色主波长为430nm，求解合成该目标色的两个色矢量的模各是多少。
解：目标色在复频谱上的色相Hp=293.616°，位于BR色域，应该用B的色矢量rb与R的色矢量rr相加合成。色矢量rb与rr合成主波长为430nm目标色的示意图如图7-7所示。
已知两色矢量的夹角φ=116.59°，α=8.6993°，β=107.86°，sin φ=0.894232，cos φ=-0.447603，tg α=0.153009。三刺激值：
=0.24769，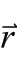
（λ）=0.00218，V（λ）=0.0116。
图7-7 色矢量rb与rr合成主波长为430nm目标色的示意图
此时假定Δθb=0.05，通过计算得到Δλb=1.94nm，则有：
B的色矢量rb=29.2251，R的色矢量rr=4.64486，由它俩合成的目标色rp的色相Hp=293.616°，波长为430nm。
例8.设目标色的主波长为410nm，求解合成该目标色的两个色矢量的模各是多少。
解：目标色在复频谱上的色相Hp=325.5°，位于BR色域，应该用B的色矢量rp与R的色矢量rr相加合成。色矢量rb与rr合成主波长为410nm目标色的示意图如图7-8所示。
已知两色矢量的夹角φ=116.6°，α=40.583°，β=76.007°，sin φ=0.894232，cos φ=-0.447603，tg α=0.856589。三刺激值：
=0.03707，
=0.00084，V（λ）=0.0012，
假定Δθb=0.05，通过计算得到Δλb=1.94nm，Δλr=0.25nm。
若设定Δλb=1.94nm，通过计算得到B的色矢量rb=35.1551，R的色矢量rr=23.5696，由它俩合成的目标色rp的色相Hp=325.5°，波长为410nm。
例9.设目标色的主波长为390nm，求解合成该目标色的两个色矢量的模各是多少。
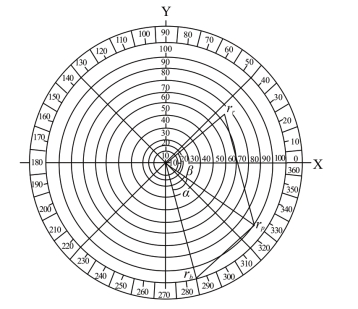
图7-8 色矢量rb与rr合成主波长为410nm目标色的示意图
解：目标色在复频谱上的色相Hp=360.65°，位于BR色域，应该用B的色矢量rb与R的色矢量rr相加合成。色矢量rb与rr合成主波长为390nm，目标色的示意图如图7-9所示。
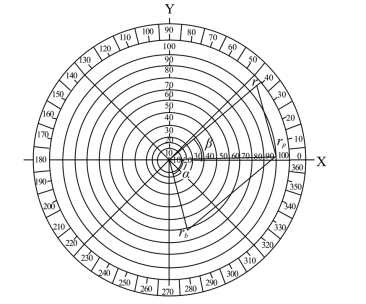
图7-9 色矢量rb与rr合成主波长为390nm目标色的示意图
已知两色矢量的夹角φ=116.6°，α=75.737°，β=40.852°，sin φ=0.894232，cos φ=-0.447603，tg α=3.93377°。三刺激值：
=0.00359，
=0.00010，V（λ）=0.00012，那么，当假定Δθb=0.05时，计算出Δλb=1.94nm。
若设定Δλb=1.94nm，通过计算得到B的色矢量rb=34.5929，R的色矢量rr=51.2544，由它俩合成的目标色rp的色相Hp=360.65°，波长为390nm。
这个目标色的色相正确的表示应该是0.65°。有意思的是它与波长780nm的相位0.33°几乎是重叠。因为波长390nm的频率正好是780nm的频率的一个倍频，所以在复频谱上两个相位是重叠的。这也表明，复频谱色谱与光谱的区别，复频谱色谱的排列是在复平面上环状首尾重合，而光谱则是首尾各处一端。这也再一次表明光与色既有联系，又有区别。
以上合成目标色的9个例题，在R、G、B每个色域中各占3例，其统计数据如表7-1所示。在每个色域的3个例题中，2个例题目标色分别靠近两个基本色中的一个基本色，1个例题居中。这样安排目的是从中看出由于目标色在两个基本色中间相位不同，致使基本色的两个色矢量模的比值也随之发生此消彼长的变化，这种变化与格拉斯曼中间色定律是一致的。
表7-1 九个例题中色矢量合成目标色有关数据
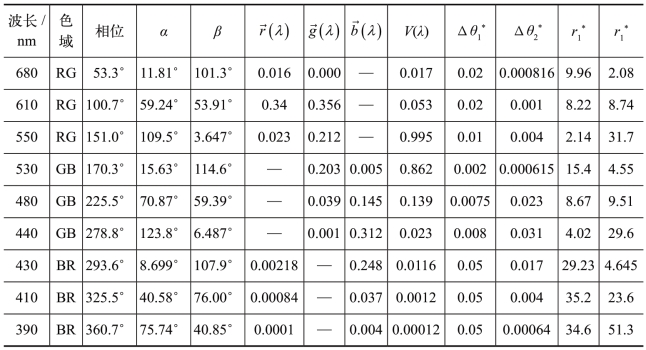
注：
*表7-1中每个波长所在色域的微弧度Δθ和色矢量r都有两个值，用下标数字“1”“2”加以区别。以该色域两个基本色中低色相者标以“1”，高色相者标以“2”。
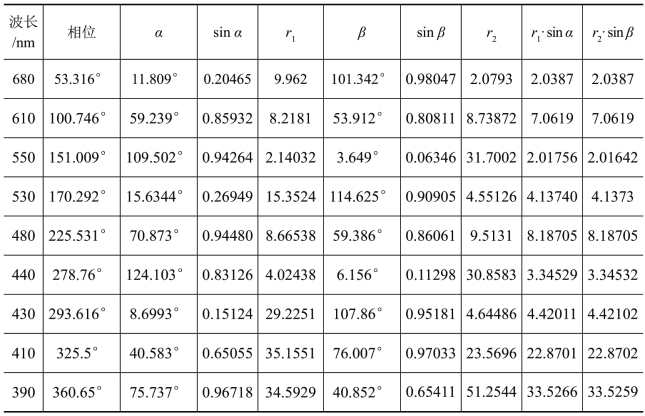
以上9个例题分别给出r1与r2两个色矢量，由于解题时预先设定的微弧度Δθ不是定值，具有一定的随意性，所以计算出来的两个色矢量r1与r2仅仅是相对值。但是只要目标色的相位是确定的，它俩的比值也是确定的，其数据只要满足三角函数中的正弦定理r1·sin α=r2·sin β就可以认为计算的结果是可以接受的，用正弦定理验证色矢量合成结果数据表如表7-2所示。
表7-2 用正弦定理验证色矢量合成结果数据表
有关光矢量变换色矢量复频谱色度理论解析的文章
- 详细阅读
-
不同冲突类型对企业目标的影响详细阅读
良性冲突是指双方目的一致而手段或途径不同的冲突。恶性冲突往往是由于双方目的不一致而造成的。这类冲突对企业目标的实现往往是不利的。趋避式冲突，又称“正负冲突”。但对冲突基本类型的了解无疑有助于进一步了解更复杂的冲突情况。组织中的非正式组织和正式组织之间、直线与参谋之间以及委员会内部之间的冲突是最为典型的团体冲突。......
2023-08-02
-
DOPO-DOPC的合成方法详细阅读
新戊二醇与三氯氧磷生成DOPC的反应和DOPO-CH2OH与DOPC的反应都是磷氯键与羟基的反应，其反应机理为SN2取代反应。将100mL三氯甲烷加入带有机械搅拌器、温度计、滴液漏斗和冷凝管的250mL四口烧瓶中，再向其中加入12.3gDOPO-CH2OH和9.225gDOPC，反应混合物加热至回流。图5-2DOPO-DOPC合成示意采用以上合成方法可以得到DOPO-DOPC，反应24h的产率可以达到88%，因此，后续合成采用以上方法，反应时间为24h。......
2023-06-26
-
不同的笑容演绎不同的心灵风景详细阅读
不同的笑容演绎不同的心灵风景表情乃是动情的一种反应，所谓动情，乃是指一个人的感情、意志等内部的精神活动，尤其是最能够反应情绪的——表面化的动作，也就是所谓的表情了。既然笑的种类繁多，那么人的笑容所表现出的心理状态就绝不是只有一种，人不仅在高兴时才笑，放心，满足，表示同意，甚至是愚弄一下对方，展现威吓、攻击时，都会出现笑容。我们知道，虽然是对同样高兴的事，各人的笑却表现出不同的形态。......
2023-12-02
-
光矢量变换色矢量复频谱色度理论解析：合成效率详细阅读
现在让合成效率ηc来回答这个问题。虽然合成效率很高，由于r1与r2相差过于悬殊，合成的中间色基本上还是趋同于r2的颜色，意义不大。从实用价值方面考虑，当r1=r2时，合成效率ηc会怎样？（8-6）式告诉我们，在两色矢量的模相同的情况下，提高合成效率的最好途径是使两色矢量r1与r2之间夹角φ变小，φ越小，合成效率越高。......
2023-11-18
-
描述流体运动的不同方法详细阅读
瑞士数学家L.欧拉大约在200多年前提出了以下两种描述流体运动的方法。拉格朗日方法采用动坐标，注意于每一流体质点的运动历史；欧拉方法采用定坐标，注意于液体运动时每一空间点处流体状态的变化。在渗流力学中通常会采用欧拉方法来描述流体运动过程中的质量、动量和能量等。......
2023-06-28
-
平面力系合成与平衡的方法分析详细阅读
平面汇交力系合成的几何法设一刚体受到平面汇交力系F1、F2、F3、F4 的作用，各力的作用线汇交于一点A。若平面汇交力系有n 个力，用FR 表示合力矢，则有合力矢对刚体的作用与原力系对该刚体的作用是等效的。图3-17几何法求约束力根据平面汇交力系平衡的几何条件，此3 个力可以组成一个封闭的三角形。......
2023-06-26
-
科技规划目标管理研究：3个案例的不同之处详细阅读
美国通过国家法律对规划目标的制定发布、组织实施、绩效报告等做出严格规定，其法制化手段是3个目标管理案例中手段最为强硬的。欧盟的目标管理机制覆盖了其28个成员国，是3个案例中目标管理机制覆盖范围最广的。表6.1发展规划目标管理典型国际经验的分析比较续表上述3个案例在目标管理机制方面的不同特点，很可能与各自的政治体制、文化传统相关。......
2023-08-05
相关推荐