复变函数和实变函数类似,同样可以讨论函数的极限和连续性,且形式基本上与实变函数一致.现在介绍复变函数的极限概念.定义3 设函数w = f(z)在点z0的去心邻域:0 ＜|z - z0| ＜ρ内有定义.如果存在一个复常数A,使得对于任意给定的ε ＞0,总存在一个实数δ ＞0(δ ＜ρ),当0 ＜|z-z0|＜δ 时,有|f(z)-A|＜ε,我们称A为f(z)当z趋于z0时的极限,记为复变函数极限的几......
2023-10-30
色相环上颜色的连续性与均匀性解析
【摘要】：颜色是由光引起的。在复频谱色度图上可辨别颜色的宽容度大约为2°。但是进一步分析，它的色相均匀性不及复频谱色度坐标上频率与相位一一对应的均匀性好。图4-6色相在频率域上的分布图4-7色相在波长域上的分布图4-6和图4-7清楚地表明了频率与波长的变化对相位角度的影响是不同的，反映在色相的均匀性上也是不同的。
当年牛顿用三棱镜将日光折射出红、橙、黄、绿、青、蓝、紫七种颜色，在紫与红之间加上紫红色，将它们排列成环状，后人称为牛顿颜色环。人们注意到，这八种颜色之中，每相邻两个颜色之间，颜色由一种过渡到另一种，用眼睛很难分辨出其变化界限。当两种颜色区别比较明显时，人们可以用红、黄、绿、蓝命名并加以区分，进一步还可以增加玫瑰红、粉红、金光红、橙黄、柠檬黄、草绿、天蓝、深蓝将其细分。但是，用命名的方法区分颜色显然不是最好的方法。
颜色是由光引起的。人类的颜色视觉最适应的是日光等热辐射光源。它辐射的是连续光谱，在该光源照射下产生的颜色，其色相的变化当然也是连续的。在连续光谱上产生的颜色，从理论上说可以有无限多种，但是凭视觉人们能够分辨出的颜色大约有180种。在复频谱色度图上可辨别颜色的宽容度大约为2°。显然，面对这么多种颜色，用命名的方法对颜色加以区分，既不容易记忆，更无法量化与计算。
光的频率是连续变化的，在复频谱上与频率对应的相位当然也是连续变化的。频率与相位有着明确的物理属性，所以我们采用相位来区分颜色，称“色相”。
在光色实验中，人们习惯采用波长标记颜色的色相或色调（hue），波长是光在某一传递介质中的基本属性之一。同一个频率的光线，通过不同介质时，其折射率不同，光速也会不同，波长则随之发生变化。所以在物理光学中，人们更习惯用光的频率表征光的基本属性，特别是在光与色的关系中，可以说频率是表征光的基本特征的本征因子。
二十世纪七十年代CIE提出的1976CIE-Luv及1976CIE-Lab两个均匀颜色空间，色调变化的均匀性有了明显改进。但是它们是在原来的CIE-XYZ色度系统波长域的基础上，通过一系列非线性坐标变换推导出来的。以CIE-Lab均匀颜色空间为例，在原来的CIE-XYZ色度系统中，色调与主频率尚存在着一定的对应关系，但在CIE-Lab色度空间里，这种对应关系不存在了。从它的色度坐标+a、-a、+b和-b来看，与十九世纪德国生物学家埃瓦尔德·赫林（Ewald Hering）提出的对立颜色学说所建立的红、绿、黄、蓝四色坐标比较接近。但是进一步分析，它的色相均匀性不及复频谱色度坐标上频率与相位一一对应的均匀性好。原因在于以下几个方面。
1.基于CIE-Lab色空间建立的a-b坐标，其色相夹角与光色矢量合成后定义出的方向无物理关联，并不具有相位的矢量特性；
2.CIE-Lab颜色空间是从CIE-XYZ非均匀颜色空间，基于人眼睛的视觉变化修正而来的，其色相分布本身就具有非均匀性；
3.在复频谱色度系统上光的频率在相位上均匀分布，而波长与频率成反比关系，因此在波长域上就不会均匀分布。
现以常用的十种油墨颜色（即复频谱色相值）在波长域和频率域分布情况加以说明。十种油墨计算出的复频谱色相值、对应的主波长和主频率统计列表如表4-3所示。
表4-3 十种油墨色相对应的波长和频率统计表
(www.chuimin.cn)
续表
上述十种油墨颜色的相位在频率域上的分布如图4-6所示，在波长域上的分布如图4-7所示。
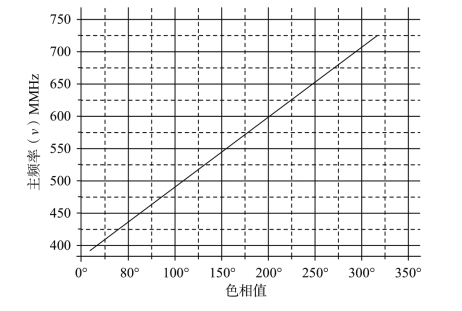
图4-6 色相在频率域上的分布
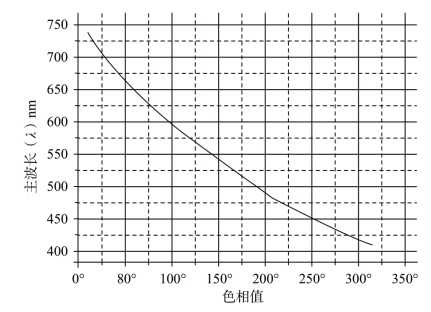
图4-7 色相在波长域上的分布
图4-6和图4-7清楚地表明了频率与波长的变化对相位角度的影响是不同的，反映在色相的均匀性上也是不同的。图4-6是等量的频率变化，对应的是等量的色相变化。而在图4-7上，例如，从650nm到750nm，波长域差为100nm，对应的色相差是57.7，而从400nm到500nm，波长域差还是100nm，对应的色相差却增到140.5，几乎是前者的两倍半。由此可见，色相在波长域分布是不均匀的，在波长较长的红色区域，色相变化较慢，颜色变化的宽容量较大，而在波长较短的蓝色区域，色相变化较快，颜色变化的宽容量较小。
如果说把色矢量作为颜色混合变化可计算的一个本征因子，那么复频谱均匀色相环则为色矢量计算提供了一个既方便又可操作的平台。
有关光矢量变换色矢量复频谱色度理论解析的文章
- 详细阅读
-
西方审美经验与生活的连续性详细阅读
对此，杜威在《艺术即经验》中言辞激越地讲道：对把美与日常生活联系起来的敌视，是一种对生活哀婉动人、情绪化甚至悲剧性的评说，说它是一种差劲的实践。[19]把审美经验与其他实践活动隔离起来，同普通大众的生活隔离起来，结果只能造就高山仰止的“博物馆艺术”。......
2024-02-01
-
函数连续性-数学与生活详细阅读
解 由于f=1，且因此函数f在点x0=0处右连续但不左连续，所以函数f在x0=0处不连续.例4 设函数讨论f在x=1处的连续性.解 由于f=2，且因此函数f在x=1处左连续且右连续，所以函数f在x=1处连续.例5 设函数问：a为何值时，函数y=f在点x=0处连续？......
2023-11-20
-
重构：学习资源与教学指导，解析非连续性文本特详细阅读
学习资源呈现的是知识与能力的结合，教学资源会对具体的知识点进行解释，同样会偏重鉴赏方法的引导。实用类文本板块同样也会侧重阅读方法层面的教学指导，例如A3-2能力层级，教师给出的相应资源是关于非连续性文本的特点和类型。首先，教师将非连续性文本与篇章文本进行对比，帮助学生认识非连续性文本。其次，谈到了非连续性文本的特征，解释其本质特征。最后，教师谈到了非连续性文本的阅读指向—信息的获取与运用。......
2023-08-06
-
归纳原理与实数连续性之等价性详细阅读
连续归纳法用于实数系是否成立，自然要依赖于实数系的基本性质。实数系与有理数系的根本不同，在于实数系的连续性。我们要证明的是命题8.2.1 连续归纳法等价于关于实数完备性的戴德金公理。设连续归纳法成立，如果已把全体实数分成了非空的甲、乙两集，而且甲集中任一个数小于乙集中的每个数，要证明的是甲集有最大数或乙集有最小数。由连续归纳法，可知px对一切x真，即一切实数x属于甲集。......
2023-10-17
-
轮胎性能：滚动阻力与均匀性的关键因素详细阅读
轮胎设计是根据特殊使用目的提供最佳性能。轮胎基本性能包括：1）轮胎滚动阻力。9）轮胎的均匀性。这种摩擦阻力占全部滚动阻力的5%～10%，并且随路面情况、轮胎结构、胎面花纹及其他因素而波动。它是轮胎滚动阻力产生的主要原因，占全部滚动阻力的90%以上。大客车、重型载货汽车及轻型载货汽车的行驶速度较低，轮胎的空气压力较高。车胎磨损后，胎面纹槽便不能尽快排除轮胎与路面的积水，也就不能防止发生浮滑现象。......
2023-08-31
-
床沙非均匀性对影响土壤渗透性的研究详细阅读
第二类方法是基于非均匀沙的某一代表粒径来计算床沙质输沙能力。式所示的概念忽略了非均匀沙的掩蔽—暴露作用，但这一作用在沙质河流中并不十分显著，因为所有非均匀沙通常均处于运动之中。式和基于D50的式 所给出的床沙质输沙率之间存在差异。这说明采用基于D50的均匀沙公式所计算的非均匀沙输沙率偏低。因此，对于非均匀沙而言，Kd作为修正因子与适合于均匀沙的输沙能力公式 联合使用，便可得到更为可靠的结果。......
2023-06-22
-
直线和圆的位置关系及其连续性详细阅读
1．直线和圆有三种位置关系：________、________、_________．设⊙O的半径为r，圆心到直线l的距离为d，则有：直线l与⊙O相交________；直线l与⊙O相切________；直线l与⊙O相离________．2．直线和圆只有__________________，我们就说直线和圆相切，这条直线叫做圆的切线，这个点叫做________．3．切线的判定：经过半径的外端且____......
2023-07-03
相关推荐