近代颜色科学的兴起-光矢量变换色矢量复频谱色度理论解析

2023-11-18 理论教育版权反馈

【摘要】：十七世纪英国天才科学家牛顿总结亲历的实验，为近代颜色科学做出了开创性的贡献。图3-1牛顿颜色环十九世纪初，英国年轻科学家杨以杨氏光干涉实验力挺光的波动说，反对牛顿的微粒说。说到颜色科学家，不能不提到格拉斯曼，他在1854年提出颜色变化的三条定律。在色彩学上称“同色异谱”。科学技术要求对颜色变化的规律给出定量的描述。

十七世纪英国天才科学家牛顿（I.Newton，1642—1727）总结亲历的实验，为近代颜色科学做出了开创性的贡献。

第一，用三棱镜把日光折射出红、橙、黄、绿、青、蓝、紫7种色光。证明了白光是由这些色光混合而成的。

第二，他说光本身是没有颜色的。光仅仅是一种能量，在光能的刺激下，视觉系统才产生颜色感觉。

第三，牛顿在1704年出版的《光学—论光的反射、折射、弯曲和颜色》（Opticks—Treatise of the Reflection Refraction Inflection and Colour）一书中指出，按照颜色红、橙、黄、绿、青、蓝、紫色相连续变化的顺序，在紫与红之间再加上一个紫红色，可以把它们排成一个封闭的圆环，人们称之为“牛顿颜色环”，如图3-1所示，从而表明颜色的色相在圆环上是连续变化的[3]。

第四，通过实验他发现，可见光中红、橙、蓝、紫4种色光之间能量的比值为红是，橙是，蓝是，紫是，其中，=1.414，=1.732，。按照现代光学理论，一个光子的能量与它的频率成正比，即ε=hν。可见光复频域两端蓝紫色光的频率为768MMHz，正好是红端频率384MMHz的两倍。因此，蓝紫端光的能量应该是红端光的能量的两倍。

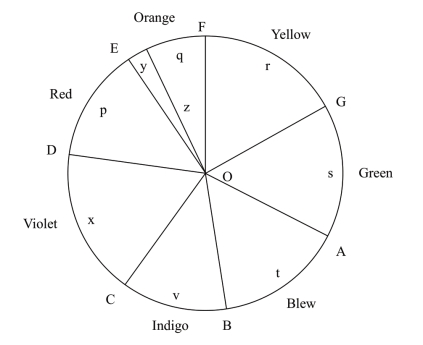
pagenumber_ebook=17,pagenumber_book=10

图3-1　牛顿颜色环

十九世纪初，英国年轻科学家杨（Thomas.Young，1773—1829）以杨氏光干涉实验力挺光的波动说，反对牛顿的微粒说。他认为牛顿所说的光的7种颜色中，只有红、绿和蓝三个颜色是原色，其他颜色都可以用这三种原色中任意两个原色混合而成。他在1801年发表的文章《关于眼睛的机理》中提出一个颜色三角原色图，见图3-2所示。

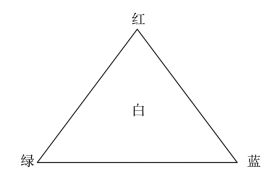
pagenumber_ebook=17,pagenumber_book=10

图3-2　Young 三角颜色图

到十九世纪六十年代，德国物理学家兼生理学家赫尔姆霍兹（Hermann.Von.Helmholtz，1821—1894），他在人的听觉和视觉两方面都做了深入研究，1868年著《生理光学》，在杨的光的三原色假说基础上，进一步推想，在人的视网膜上分布着三种神经纤维。即感红光纤维、感绿光纤维和感蓝光纤维，如图3-3所示。如果只受一种原色光的刺激，只产生该种颜色感觉；如果同时受到两种原色光的刺激，则产生两种原色光混合的感觉。如果红、绿、蓝三种光同时刺激，就会产生白色感觉。把他们二人的观点综合起来，就是今天大家熟知的杨−赫三原色假说。[4]

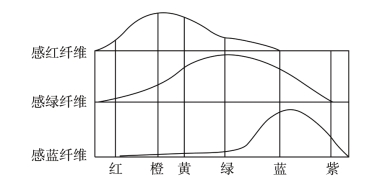
pagenumber_ebook=18,pagenumber_book=11

图3-3　Helmholtz 三色感光纤维

有人说赫尔姆霍兹是位医生，其实他首先是一位出色的物理学家兼生理学家。他借数学傅里叶变换研究人的听觉，人耳可以把多种音频混合的声音，分解出不同频率。他用频谱分析的方法，指出音乐之所以悦耳，因为音乐有谐频，不仅增强了音量，还丰富了音色。他试图用同样频谱分析的方法解释颜色，却发现可见光里没有谐频，他不无遗憾地说，与耳相比，眼睛在这方面没有音乐。鉴于当时的科学水平，人们对光的本性的认识，尚不足以把光与色的内在联系揭示出来。但是，今天不同了，可见光虽然没有谐频，用频谱分析的方法在光学传递函数方面已取得了成功，在通信信号处理方面也取得了成功，进一步来说，在光色变换复频谱颜色处理方面证明也是成功的。(www.chuimin.cn)

说到颜色科学家，不能不提到格拉斯曼（H.Grassman，1808—1877），他在1854年提出颜色变化的三条定律。第一，颜色具有色相、明度、饱和度三个独立的属性。第二，每一种颜色都存在一个与之对应的补色。一对互补色以适当比例混合，便产生中性色。两个非互补色混合，产生它们的中间色相。中间色相的位置倾向二者中分量较多的一边。混合后颜色的饱和度，取决于两个色相距离的远近。距离越远，饱和度越低。第三，两个颜色虽然它们的光谱结构不同，只要在视觉上颜色相同，就可以视作同色。在色彩学上称“同色异谱”。现代的彩色印刷、彩色电视及彩色照相等色彩再现技术，都是不追求色的光谱结构相同，只追求颜色相同，所以说格拉斯曼的颜色三定律今天仍然是颜色科学的理论基础。

格拉斯曼不仅提出了颜色变化的三大定律，他还指出颜色具有矢量性质。其实从他指出的颜色属性中第二条两个非互补色混合产生中间色来看，正好与矢量合成中的正弦定律即杠杆定律相符合。今天复频谱颜色理论的核心是色矢量，包括色光混合和色料混合完全是色矢量合成的结果。遗憾的是，格拉斯曼的这一重要观点被忽略了。

凡是具有正常视觉的人，都能在光照下感知颜色，但是人的这种感知只能是相对的、定性的。二十世纪以来科学技术的进步，使人们感到仅靠人眼对颜色做出定性判断已不能适应现实的需要。科学技术要求对颜色变化的规律给出定量的描述。

二十世纪二十年代莱特（W.D.Wright）、吉尔德（J.Guild）等多位科学家在杨－赫三原色假说基础上，用红（R）、绿（G）、蓝（B）三原色光做了大量视觉色光匹配光谱色实验。国际照明委员会（CIE）在他们实验的基础上，正式采用红光700nm，绿光546.1nm及蓝光435.8nm三个准单色光作为基本色光，以调节光亮度的方法匹配目标光谱色，制定了CIE1931-RGB系列颜色坐标系统及1931CIE-XYZ色度坐标系统，为颜色科学开创了一个新的发展空间。由于彩色电视、彩色摄影（像）及彩色印刷、彩色显示等技术的进步，才使得今天的世界进入一个新的彩色文明时代。无疑，杨－赫的三原色假说功不可没。

实践是对科学最好的检验，在长期大量实践中，人们也发现有些现象和问题还无法给出科学合理的解释。三色理论的基础是说在人的视网膜上分布着感红、感绿和感蓝三种不同的锥体感光细胞。可是“就人类视网膜细胞而言，目前还不可能分开和确定那些光敏细胞上的色素，有关描述锥体细胞光敏感光性的确切曲线形状仍然是个有争论的问题”[5]。本书作者认为，某频率可见光刺激视觉锥细胞产生的信号没有必要变为基本色信号，而是直接变成按相位分布的色矢量信号，再由这些色矢量合成出颜色。

人们希望从理论上讲，红、绿、蓝三个原色光等能量混合应该显示白色，可是在用红、绿、蓝三个单色光人工视觉匹配白光实验中发现，匹配等能白光红、绿、蓝三原色的亮度比例为：1.0000∶4.5907∶0.0601；它们的辐亮度的比例为：79.0962∶1.3791∶1.0000，特别是辐亮度，在能量层级上并不是1∶1∶1。又如太阳光谱，在不同频率处，能量不一定都相等，但是太阳光视觉呈现白光，这些都还没有给出合理的解释。更为重要的是，现代光学理论认为电磁波的复振幅，光子的动量均呈矢量特性，然而在杨－赫的三原色假说中却没有反映出颜色的矢量特性，因此对于色光相加的白平衡，色料相减的灰平衡，以及颜色合成中的中间色定理（杠杆定理）人们只能从实验中去认识，无法给出矢量解释。

大家最熟悉彩色电视，在彩色画面上经常看到由红基色和蓝基色合成的鲜艳的紫红颜色，可是在1931CIE-XYZ色度坐标图上，从中心白点分别到700nm红色坐标点和400nm蓝色坐标点，形成一个三角形色域，称紫红色域。紫红色在自然界也是客观存在的，可是在这个色度图上它不是光谱色域的颜色，因而它没有主波长。既然色与光在波长域有着一一对应的关系，没有主波长，表明暂时还不清楚紫红色物理光学归属。

如果不考虑电磁波在空间的位置与其初相位α，电磁波的波函数可以表示为E=E0eiωt。可是对于人的颜色视觉来说，时间t肯定不是变量，而是个常量T。这样一来，电磁波的波函数中的变量就只有振幅E0和频率v（ω=2πv）了。当t=T，则2πvT=θ，这样波函数E=E0eiθ，完全可以在二维复平面上作矢量解析。可是颜色三个属性：色相、亮度、饱和度却被看作三个完全独立的属性，必须用三维立体空间来表示。按逻辑推理，既然光在视觉上是二维的，色也应该是二维的，那么颜色三属性中至少有一个不是独立的。后面在复频谱颜色解析中就会明白，颜色的色相是处在色矢量的层级上，而色矢量平方后积分对应的是光的相对能量，也就是亮度对应的是能量，色相对应的是色矢量，两个不在一个层级上。那么，颜色的亮度对色相来说在复平面上，它就不是独立的了。

光学是一门既古老又年轻的学科。说它古老，是因为从人类古文明开始就有对它的探索；说它年轻，是因为直到二十世纪开始人们对光的本性的认识，才有了一个很大的飞跃，认识到光具有波粒二象性。十七世纪牛顿把光线看作一种微粒射线（rays），坚持光的微粒说。到十九世纪杨通过干涉实验有力地证明了光具有波动性，支持光的波动说。到十九世纪中期，麦克斯韦（Jams.Maxwell，1831—1879）证明了光就是电磁波，推动科学界对光的波动性有了更深入的认识。二十世纪初德国物理学家，现代量子理论奠基人之一普朗克（Max.Planck，1858—1947）（顺便说一下，果然名师出高徒，他正是三原色理论创始人之一赫尔姆霍兹的学生），于1900年在研究黑体辐射时，发现一些问题，于是大胆提出一个假设：一个原子谐振子吸收或者发射一个一个不连续的能量，这个能量正比于它的频率v。1905年，二十世纪伟大的科学家爱因斯坦（Albert.Einstein，1878—1955）通过光电效应，肯定了普朗克的假说，进一步断定光的能量是由一个一个小粒子组成，一个粒子的能量ε=hv，h称普朗克常数h=6.626176× 10-34JS。如果有m个粒子，那么εm=mhv，m是正整数。后来大家把这个粒子称为“光子”。光子是以电磁波的速度在传播，光子的静止质量为零，在运动中以动量的方式与电子作用，转化为能量。一个光子的动量P=，动量是矢量。从二十世纪初光子理论到此后二三十年代，在丹麦物理学家玻尔（Niels.Bohr，1855—1962）、奥地利物理学家薛定谔（E.Schrödinger，1887—1961）、法国物理学家德布罗意（L.De-Broglie，1892—1987）及德国物理学家玻恩（Max.Born，1882—1970）等多位科学家的共同努力下，终于揭开了蒙在古老光学上面的面纱。单个光子在空间的位置虽然无法确定，但大量光子的概率分布就可以给出一个确定的结果，某一点光子出现的概率正比于该点光波振幅的平方，这就是光子的概率密度。联系到人的颜色视觉，当数以万计的光子同时进入眼睛，光的波函数中振幅的平方，即|E|2也可以看作光子出现的概率密度。这样，眼睛对于入射光无论是振幅还是光子数，就把光的波动性与粒子性很好地统一起来。原本在视觉里，光既显波动性，又显粒子性，在复频谱颜色理论里，统一了光的波粒二象性，即说它有波动性，光有波长、频率和振幅，它以电磁波的形式传播；说它有粒子性，光子的能量是一份一份的，一个光子的动量P=，显然光子在辐射或被吸收过程中表现出的是粒子特性。光当然是一种矢量，电场和磁场都是矢量场，光的复振幅随相位变化，也是矢量，光子的动量也是矢量。既然光与色具有紧密的相关联系，那么说颜色也具有矢量性是可以理解了。

这场光学新思想革命发生的时间从二十世纪初到三十年代，其影响大多局限在少数物理学家范围内。而莱特、吉尔德等颜色科学家做的光色匹配实验恰恰也在这个时代。本来应该是光与色两个有着紧密联系的科学成就，却阴差阳错擦肩而过，实在是颜色科学的一件憾事。

光与色的关系实在是太密切了，可以说光与色是形影相随。光的复振幅的矢量特性映射出颜色的矢量特性，复频谱光与色的关系：光的频率映射在复频谱上就是颜色的相位，光量的强弱映射出颜色的明暗程度。既然颜色的特性是源于光的特性，那么逆推过来，也可以从光的特性推导出颜色的特性。今天回顾这段历史，是想说复频谱颜色理论正是在先辈们颜色与光的理论基础上产生的。可以说，没有先辈们颜色科学的大量实践，没有光的波粒二象性的现代光学的理论基础，没有积分变换的数学工具，就不会有今天的复频谱颜色理论的产生。

本书中复频谱的定义是：以可见光红端频率384MMHz为基频，蓝紫端频率768MMHz为一个倍频，对应波长为390～780nm，这个频域里的可见光变换的色矢量均匀地分布在0～2π（0°～360°）相域内。

近代颜色科学的兴起-光矢量变换色矢量复频谱色度理论解析

相关推荐