之后计算求得该组5个制品减重百分数的平均值xi，作为该组实验的结果。表6-9 实验结果表6-10 实验结果表6-11 实验结果表6-9～表6-11中，每一行为一组实验数据，各因素下为对应的水平号。表6-10～表6-11中实验号5、13、14的实验结果明显小于其他数据，后续数据处理中保留了这些数据，没有作为奇异项处理。图6-32 一个注塑周期的实验数据图所有数据统一在一个时间轴下记录，为后续数据分析提供了便利。......
2023-07-02
实验科学研究、开发投入与产出的相关分析
【摘要】：近些年来，我国科学技术创新取得了重大进展，从研发投入、研发人员、论文、专利数量以及重大科技成果产出来看，我国科技实力得到巨大提升．无论是科学研究还是技术创新，都表现出很强的跟进和创新能力，追赶的步伐不断加快，在一些重要科研领域正在从“量变”走向“质变”，在一些新的科技竞争制高点上也占有一席之地．但是，我国与发达国家的科技实力还存在一定的差距，产生这种差距的原因何在？
近些年来，我国科学技术创新取得了重大进展，从研发投入、研发人员、论文、专利数量以及重大科技成果产出来看，我国科技实力得到巨大提升．无论是科学研究还是技术创新，都表现出很强的跟进和创新能力，追赶的步伐不断加快，在一些重要科研领域正在从“量变”走向“质变”，在一些新的科技竞争制高点上也占有一席之地．但是，我国与发达国家的科技实力还存在一定的差距，产生这种差距的原因何在？我们以下从科技投入与产出方面来具体了解我国科研与开发机构的科技活动情况，以期找到原因所在．
表12-2给出了我国科研与开发机构科技投入与产出的部分代表指标（费宇，2014）．其中，科技投入指标为：R&D 人员全时当量x1（单位：万人年），R&D 经费支出x2（单位：亿元），政府资金x3（单位：亿元），企业资金x4（单位：亿元）；科技产出指标为：发表科研论文y1（单位：篇），专利申请受理y2（单位：件），发明专利y3（单位：件）．应用这些数据进行典型相关分析来研究我国科研与开发机构科技投入与产出的关系．
表12-2 我国科学研究与开发机构科技投入与产出情况表
（1）根据表12-2导入数据
＞x1＝c(20．4,20．3,21．5,23．1,25．5,26．0,27．7,29．3,31．6,34．4)
＞x2＝c(399．0,431．7,513．1,567．3,687．9,811．3,996．0,1186．4,1306．7,1548．9)
＞x3＝c(320．3,344．3,424．7,481．2,592．9,699．7,849．5,1036．5,1106．1,1292．7)
＞x4＝c(20．8,22．4,17．6,17．3,26．2,28．2,29．8,34．2,39．9,47．4)
＞y1＝c(97500,104699,109995,118211,126527,132072,138119,140818,148039,158647)
＞y2＝c(4836,5464,6814,8026,9802,12536,15773,19192,24059,30418)
＞y3＝c(1393,1972,2088,2191,2467,3102,4077,5249,7862,10935)
＞X＝data．frame(x1,x2,x3,x4,y1,y2,y3)
（3）把数据标准化后求典型相关系数
＞xy＝scale(X)
＞ca＝cancor(xy[,1：4],xy[,5：7])
＞ca＄cor
[1]0．9996747 0．9248488 0．6972691
（4）x 的典型载荷
（5）y 的典型载荷
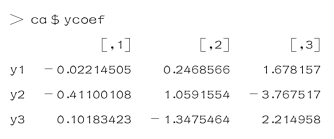(www.chuimin.cn)
（6）相关系数的检验
以上结果说明，前两对典型相关变量通过了相关系数的检验．
根据x 的典型载荷和y 的典型载荷的结果，前两对典型相关变量的表达式为
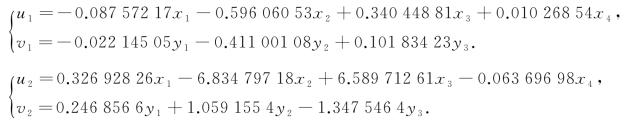
经过典型相关系数的显著性检验，可知需要前两对典型变量，即在显著性水平为0．05时，前两个典型相关是显著的．我们利用前两对典型变量分析问题，达到了降维的目的，第一对典型变量的相关系数为0．999 674 7，第二对典型变量的相关系数为0．924 848 8，说明u1 和v1 以及u2 和v2 之间具有高度的线性相关关系．
在第一对典型变量u1 和v1 中，u1 为我国科研与开发机构科技投入指标的线性组合，其中x2（R&D 经费支出）和x3（政府资金）相对其他变量有较大的载荷，说明科技经费和政府资金在科技投入中占主导地位；x3（政府资金）相对x4（企业资金）有较大的载荷，说明我国科研与开发机构的科技活动中，政府资金所做的贡献大于企业资金，政府资金的激励作用更大；同时x2 （R&D 经费支出）相对x1（R&D 人员全时当量）有较大的载荷，说明科技投入过程中，经费所起的作用大于人员的作用．v1 为我国科研与开发机构科技产出指标的线性组合，其中y2 （专利申请受理）和y3（发明专利）相对其他变量有较大的载荷，说明专利申请受理和发明专利对科研与开发机构科技产出贡献很大．
在第二对典型变量u2 和v2 中，u2 为我国科研与开发机构科技投入指标的线性组合，其中仍然是x2（R&D 经费支出）和x3（政府资金）有较大的载荷，v2 为我国科研与开发机构科技产出指标的线性组合，其中y2（专利申请受理）和y3（发明专利）有较大的载荷．
第二对典型变量与第一对典型变量载荷比重情况相似，但符号有较大差异．
（7）画得分等值平面图
＞u＜-as．matrix(xy[,1：4])%∗%ca＄xcoef
＞v＜-as．matrix(xy[,5：7])%∗%ca＄ycoef
＞par(mfrow＝c(1,2))
＞plot(u[,1],v[,1],xlab＝＂u1＂,ylab＝＂v1＂)
＞abline(0,1)
＞plot(u[,2],v[,2],xlab＝＂u2＂,ylab＝＂v2＂)
＞abline(0,1)
运行的结果如图12-2所示．
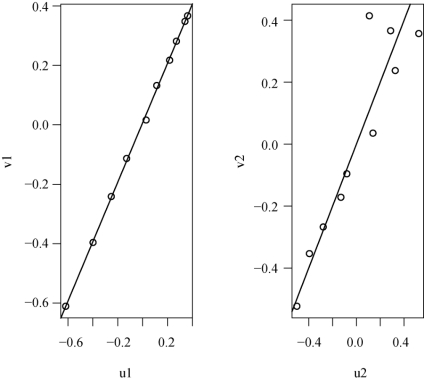
图12-2 得分等值平面图
从图12-2可以看出，第一对典型变量的得分散点近似在一条直线上分布，两者之间呈高度线性相关关系，散点图上没有离开群体的差异点．第二对典型变量的得分散点也近似在一条直线上分布，虽有偏离情况发生，但总体上还是呈现出了线性相关关系．
综合第一对典型变量和第二对典型变量来看，我国科研与开发机构的科技投入与产出之间的关系很稳定，整体平稳．
有关应用多元统计分析：基于R的实验的文章
- 详细阅读
-
柴油机热流相关性分析及实验结果分析详细阅读
柴油机的热流测量方法与汽油机类似。柴油机也同样表现为每个循环的热流曲线之间有很大的变化。试验条件是压缩比为16，转速为2000r/min，当量比为φ=0.5，进气系统压力为1.5×105Pa。图8-20 中间涡流柴油机热流涡流较小的柴油机活塞凹部的平均热流通常比活塞冠部环状壁部位和气缸盖部位的平均热流高。图8-21 自然进气柴油机的气缸盖与气缸套处热流Praum计算求出活塞壁面与气缸盖面的热传递率h1，以及气缸套面的热传递率h2，并比较判定后者为前者的1/3，即h2=1/3h1......
2023-06-28
-
《形式化开发多序列比对算法》实验结果与分析详细阅读
本实验采用C++语言，使用VS2019集成开发环境。替换矩阵采用Clustal W中默认的IUB矩阵。最终比对结果与Clustal W和Clustal O的比对结果，如图5-7所示。图5-7算法结果比较通过对PAR方法和PAR平台的使用，我们运用Apla语言以半自动的方式组装形成了基于系统发生树的渐进式比对算法，并将Apla程序转换成了C++代码，得到了可运行的算法程序，算法结果与Clustal W和Clustal O进行了比较，基本的保守位点和相似区域都可有效发现，具有一定的生物学意义。......
2023-10-25
-
空间相关性分析：方法与应用详细阅读
图6.25入室盗窃犯罪数量分时间分区域统计图为探明哪些社会经济指标对抗议事件的发生有影响，哪些指标的影响是正面的，哪些指标的影响是负面的，本研究使用了栅格数据相关性分析方法。图6.27栅格相关性分析矩阵由于相关矩阵的对称性，可以用三角矩阵的形式描述相关性。......
2023-06-15
-
典型相关分析基本思想与应用详细阅读
典型相关分析是仿照主成分分析法中把多变量与多变量之间的相关化为两个变量之间相关的做法，首先在每组变量内部找出具有最大相关性的一对线性组合，然后再在每组变量内找出第二对线性组合，使其本身具有最大的相关性，并分别与第一对线性组合不相关．如此下去，直到两组变量内各变量之间的相关性被提取完毕为止．有了这些最大相关的线性组合，则讨论两组变量之间的相关，就转化为研究这些线性组合的最大相关，从而减少了研究变量的......
2023-11-18
-
对比分析计算与实验结果详细阅读
峰值应力和破坏应变的相对误差小于5.13%。图8－18动能与内能之比表8－2不同单元尺寸下的峰值应力和失效应变Wu 等［8］和Rangaswamy 等［17］测量得到的PBX 9501 拉伸和压缩应力－应变曲线用于校准不同应变速率下的模拟结果。破坏应变分别为0.011 7、0.011 8 和0.012，与实验测得的0.011 7、0.011 9 和0.012 2 的破坏应变比较接近。图8－19测量和计算的应力－应变曲线拉伸；压缩应变率为10－4s－1；压缩应变率10－3s－1；压缩应变率10－2s－1......
2023-06-27
-
分析整理相关材料的方法与步骤详细阅读
分析整理与公共关系策划相关的材料,是公共关系策划一般过程的首要环节。准确、有效、及时的信息是公共关系策划的重要依据。材料分析是在广泛收集有关材料的基础上,抽取出与公共关系策划直接相关的各种材料。将已获取的信息,根据去粗取精、去伪存真、由此及彼、由表及里的工作方法,综合提炼出对公共关系策划具有价值的材料。将第二阶段处理的材料,通过分类整理,编制成各种资料归类存档。......
2023-07-16
-
关于变量相关关系的探讨与分析详细阅读
以两个变量为例进行讨论。这种关系x与y的关系点杂乱无章，如图X3.15所示。相关关系，指两个变量x与y之间的关系介于完全相关和零相关之，这种关系x与y的关系点呈带状分布趋势，如图X3.16所示。图X3.15零相关示意图图X3.16相关关系示意图直线相关；曲线相关例如，流域年径流深与年降水量之间的关系，就是相关关系。......
2023-06-21
相关推荐