,F5 的线性组合表示出来Xi=μi+ai1 F1+ai2 F2+…,F5 的值却是未知的,有关参数的意义也有很大的差异.因子分析的首要任务就是估计因子载荷aij 和方差σ2i,然后给因子Fi 一个合理的解释,若难以进行合理的解释,则需要进一步作因子旋转,希望旋转后能发现比较合理的解释.特别需要说明的是这里的因子和试验设计里的因子(或因素)是不同的,它比较抽象和概括,往往是不可以单独测量的.......
2023-11-18
实际问题中,需要考虑两组变量之间的相关关系的问题很多,例如,考虑几种主要产品的价格(作为第一组变量)和相应这些产品的销售量(作为第二组变量)之间的相关关系;考虑投资性变量(如劳动者人数、货物周转量、生产建设投资等)与国民收入变量(如工农业国民收入、运输业国民收入、建筑业国民收入等)之间的相关关系;等等.
复相关系数描述两组随机变量X=(x1,x2,…,xp)T,Y=(y1,y2,…,yq)T 之间的相关程度.其思想是先将每一组随机变量作线性组合,成为两个随机变量:
再研究u 与v 的相关系数.由于v,u 与投影向量ρ,γ 有关,所以ruv=ruv(ρ,γ).取在ρTΣXXρ=1和γTΣYYγ=1的条件下使ruv 达到最大的ρ,γ 作为投影向量,这样得到的相关系数为复相关系数
ruv=max ruv(ρ,γ).
此时
因此,问题转化为在ρTΣXXρ=1 和γTΣYYγ=1 的条件下求ρTΣXYγ 的 极大值.
根据条件极值法引入Lagrange乘数,可将问题转化为求
的极大值,其中λ,ω 是Lagrange乘数.
由极值的必要条件得方程组
将上两式分别左乘ρT 与γT,则得
注意![]() ,所以λ=ω=ρTΣXYγ.
,所以λ=ω=ρTΣXYγ.
代入方程组(12.2.1)得到
用![]() 左乘方程组(12.2.2)的第二式,得
左乘方程组(12.2.2)的第二式,得![]() ,所以
,所以
代入方程组(12.2.2)的第一式,得
同理可得
记
则有
式(12.2.4)说明λ2 既是M1 又是M2 的特征根,ρ,γ 就是其相应于M1 和M2的特征向量.M1 和M2 的特征根非负,均在[0,1]上,非零特征根的个数等于min(p,q),不妨设为q.
设M1ρ=λ2ρ 的特征根排序为![]() ,其余p-q 个特征根为0,称λ1,λ2,…,λq 为典型相关系数.相应地,从M1ρ=λ2ρ 解出的特征向量为ρ(1),ρ(2),…,ρ(q),从M2γ=λ2γ 解出的特征向量为γ(1),γ(2),…,γ(q),从而可得q对线性组合(www.chuimin.cn)
,其余p-q 个特征根为0,称λ1,λ2,…,λq 为典型相关系数.相应地,从M1ρ=λ2ρ 解出的特征向量为ρ(1),ρ(2),…,ρ(q),从M2γ=λ2γ 解出的特征向量为γ(1),γ(2),…,γ(q),从而可得q对线性组合(www.chuimin.cn)
ui=ρ(i)T X,vi=γ(i)T Y,i=1,2,…,q,
称每一对变量为典型变量.求典型相关系数和典型变量归结为求M1 和M2 的特征根和特征向量.
还可以证明,当i≠j 时,有
Cov(ui,uj)=Cov(ρ(i)T X,ρ(j)T X)=ρ(i)TΣXXρ(j)=0,
Cov(vi,vj)=Cov(γ(i)T Y,γ(j)T Y)=γ(i)TΣYYγ(j)=0,
表示一切典型变量都是不相关的,并且其方差为1,即
Cov(ui,uj)=δij,
Cov(vi,vj)=δij,
其中
X 与Y 的同一对典型变量ui 和vi 之间的相关系数为λi,不同对的典型变量ui 和vj(i≠j)之间不相关,也就是说协方差为0,即
当总体的均值向量μ 和协差矩阵Σ 未知时,无法求总体的典型相关系数和典型变量,因而需要给出样本的典型相关系数和典型变量.
设X(1),X(2),…,X(n),Y(1),Y(2),…,Y(n)为来自总体容量为n 的样本,这时协方差矩阵的无偏估计为
其中![]() ,用
,用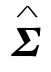 代替Σ 并按式(12.2.3)和式(12.2.4)求出
代替Σ 并按式(12.2.3)和式(12.2.4)求出 和
和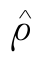 ,
, ,称
,称 为样本的典型相关系数,称
为样本的典型相关系数,称![]() (i=1,2,…,q)为样本的典型变量.
(i=1,2,…,q)为样本的典型变量.
计算时也可从样本的相关系数矩阵出发求样本的典型相关系数和典型变量,将相关系数矩阵取代协方差阵,计算过程是一样的.
如果复相关系数中的一个变量是一维的,那么也可以称为偏相关系数.偏相关系数是描述一个随机变量y 与多个随机变量(一组随机变量)X=(x1,x2,…,xp)T 之间的关系.其思想是先将那一组随机变量作线性组合,成为一个随机变量
再研究y 与u 的相关系数.由于u 与投影向量c有关,所以ryu=ryu(c)与c有关.我们取在cTΣXX c=1的条件下使ryu 达到最大的c 作为投影向量得到的相关系数为偏相关系数
ryu=max ryu(c).
其余推导、计算过程与复相关系数类似.
有关应用多元统计分析:基于R的实验的文章

,F5 的线性组合表示出来Xi=μi+ai1 F1+ai2 F2+…,F5 的值却是未知的,有关参数的意义也有很大的差异.因子分析的首要任务就是估计因子载荷aij 和方差σ2i,然后给因子Fi 一个合理的解释,若难以进行合理的解释,则需要进一步作因子旋转,希望旋转后能发现比较合理的解释.特别需要说明的是这里的因子和试验设计里的因子(或因素)是不同的,它比较抽象和概括,往往是不可以单独测量的.......
2023-11-18

多元统计分析是统计学中应用性很强的一个分支,它的应用范围十分广泛.多元统计分析可以应用于几乎所有的领域,主要包括经济学、农业、地质学、医学、工业、气象学、金融、精算、物理学、地理学、军事科学、文学、法律、环境科学、考古学、体育科学、遗传学、教育学、生物学、管理科学、水文学等,还有一些交叉学科或方向等.多元统计分析的应用实在是难以一一罗列,以下简要地介绍一下多元统计分析在文学、数据挖掘(作为交叉学科......
2023-11-18

根据上面的叙述,要选择样本空间Ω 的一个划分R1 和R2=Ω-R1,使得平均误判损失ECM 达到极小.定理8.3.1 极小化平均误判损失式的区域R1 和R2 为说明:当时,即x 为边界点,它可以归入R1 和R2中的任何一个,为了方便就将它归入R1.根据定理8.3.1,得到两总体的Bayes判别准则:应用此准则时仅需要计算:新样本点x0=(x01,x02,…......
2023-11-18

如果是,建立变量之间的定量关系式,并用于预测或控制——回归分析.变量之间的相互关系:分析两组变量之间的相互关系——典型相关分析.多元数据的统计推断这是关于参数估计和假设检验的问题.特别是多元正态分布的均值向量和协方差矩阵的估计和假设检验等问题.多元统计分析的理论基础多元统计分析的理论基础包括多维随机向量,以及由此定义的各种多元统计量,推导它们的分布并研究其性质,研究它们的抽样分布理论.......
2023-11-18

,βp的线性函数.因此,对μ 作变换,则可得到下面几种分布的连接函数的形式:正态分布m(μ)=μ=∑βi xi.二项分布.Poisson分布m(μ)=lnμ=∑βi xi.上述推广体现在以下两个方面:通过一个连接函数,将响应变量的期望与解释变量建立线性关系m[E]=β0+β1 x1+β2 x2+…......
2023-11-18

,n)总的分散程度,对SST 进行分解,得到其中,.可以证明,,由此得其中,.SSR 叫做回归平方和,由于所以SSR 是回归值 的离差平方和,它反映了yi(i=1,2,…......
2023-11-18

随着大数据、人工智能在我们日常生活的渗透,学习多元统计分析的人越来越多.“多元统计分析”课程已经被越来越多高校列为相关专业的必修课或选修课.《多元统计分析》教材的特点各有不同,有的教材侧重理论的讲述,读者需要具备较深厚的数学基础;有的教材则注重模型的应用,理论和技术细节不是重点.作者认为,对于侧重“应用”多元统计方法进行数据处理和分析的读者,重点不在于理解多元统计方法的理论证明和公式推导,而是要应......
2023-11-18

用MASS包中的UScereal数据集,我们研究美国谷物中的卡路里、脂肪和糖含量是否会因为储存架位置的不同而发生变化.其中1代表底层货架,2代表中层货架,3代表顶层货架.卡路里(calories)、脂肪(fat)和糖(sugars)含量是因变量,货架是3水平(1,2,3)的自变量.(1)单因素多元方差分析在以上代码中,“cbind( )”函数将三个变量(calories,fat,sugars)合并......
2023-11-18
相关推荐