大致说来,摩尔和奥斯汀主要是语言分析,赖尔和斯特劳森主要是逻辑分析,维特根斯坦的分析最复杂,涉及的范围最广,包括的东西也最多。赖尔主要是通过具体的语言实例进行分析,而斯特劳森主要是通过句法形式进行分析。......
2024-01-22
原教材中用MATLAB给出了美国授予哲学博士学位的对应分析,现在用R来进行对应分析.
表11-1的数据是美国在1973年到1978年间授予哲学博士学位的数目(美国人口调查局,1979年),试用对应分析方法分析该组数据.
如果把年度和学科作为两个属性变量,年度考虑1973年至1978年这6年的情况(6个类目),学科也考虑6种学科,那么表11-1就是一张两个属性变量的列联表.
本实验采用两种方法,分别对表11-1中的数据进行对应分析.
表11-1 美国1973年—1978年间授予哲学博士学位的数据
方法1:
(1)根据表11-1导入数据并进行χ2 检验——考察行变量和列变量是否独立
>x1=c(4489,4101,3354,2444,3338,1222)
>x2=c(4303,3800,3286,2587,3144,1196)
>x3=c(4402,3749,3344,2749,2959,1149)
>x4=c(4350,3572,3278,2878,2791,1003)
>x5=c(4266,3410,3137,2960,2641,959)
>x6=c(4361,3234,3008,3049,2432,959)
>X=data.frame(x1,x2,x3,x4,x5,x6)
>rownames(X)=c("L","P","S","B","E","M")
>chisq.test(X)
结果如下:

由于p 值远小于0.05,所以行变量和列变量不独立,即6个行点(学科)和6个列点(年份)有密切关系,可以进一步进行对应分析.
(2)计算行列得分
>library(MASS)
>ca2=corresp(X,nf=2)
>rownames(X)=c("L","P","S","B","E","M")
>ca2
结果如下:
 (www.chuimin.cn)
(www.chuimin.cn)
(3)作对应分析图
>biplot(ca2);abline(v=0,h=0,lty=3)
结果如图11-1所示.
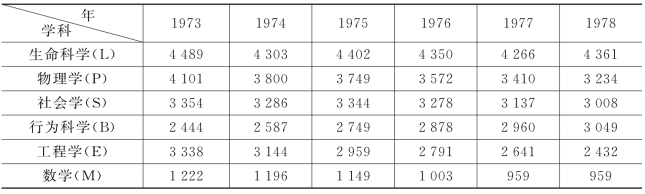
图11-1 行点和列点的散点图
在图11-1中x1,x2,x3,x4,x5,x6 分别代表1973,1974,1975,1976,1977,1978年的数据.
分析行点和列点的散点图时主要看两种散点的横坐标之间的距离(纵坐标的距离对于分析意义不大).
由图11-1可看出,6个行点(学科)和6个列点(年份)可以分为三类(其对应关系如下):第一类包括“行为科学(B)”,它在1978年授予的博士学位数目的比例最大;第二类包括“社会学(S)”和“生命科学(L)”,它们在1975年至1977年授予的博士学位数目的比例都是逐年下降;第三类包括“物理学(P)”“工程学(E)”和“数学(M)”,它们在1973年和1974年这两年授予的博士学位数目的比例最大.
以上结果与原教材中用MATLAB给出的结果是一致的.
方法2:
(1)(如果已导入数据)进行对应分析
>library(ca)
>a<-ca(X)
>a
结果如下:

在以上结果中,Dim.1和Dim.2是提取的两个因子对行、列变量的因子载荷(行列得分).
(2)使用函数“plot( )”提取对应分析的结果——画散点图
>plot(a)
结果如图11-2所示.
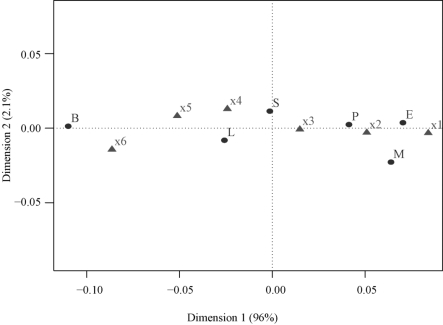
图11-2 行点和列点的散点图
在图11-2中x1,x2,x3,x4,x5,x6 分别代表1973,1974,1975,1976,1977,1978年的数据.
由图11-2可看出,6个行点(学科)和6个列点(年份)可以分为三类,其对应关系与方法1相同.
以上的方法1和方法2的结果是一致的(方法1中的行列得分与方法2中的Dim.1和Dim.2是一致的,图11-1和图11-2也是一致的),并且它们都与原教材中用MATLAB给出的结果是一致的.
有关应用多元统计分析:基于R的实验的文章

大致说来,摩尔和奥斯汀主要是语言分析,赖尔和斯特劳森主要是逻辑分析,维特根斯坦的分析最复杂,涉及的范围最广,包括的东西也最多。赖尔主要是通过具体的语言实例进行分析,而斯特劳森主要是通过句法形式进行分析。......
2024-01-22

[6]对中国私募基金最早的调查报告见夏斌。[11]见史文森,第187页,253页。据说收取20%业绩提成费的惯例是对冲基金创始人琼斯从另一类交易中得到的灵感。[18]见肖欣荣、田存志第123页注释1。[19]见肖欣荣、田存志第129页正文最后一段。在实践中一般要求高于10年期债券的收益率。一方面,公募基金由审批制变为核准制;私募基金完全自主发行。另外一方面,基金销售目前是买方市场。......
2023-07-22

杰克逊的反对派将自己称为“国民共和党”,后来简称“辉格党”。辉格党只是将哈里森作为属于人民的代表推荐给全国人民,同时攻击范布伦是东部贵族。在这次力量博弈中,主张设立国家银行、坚挺的货币和高额保护关税的辉格党被彻底击垮,民主党人取得了决定性的胜利。种植园主的代表们开始在农场主、工匠和一般劳工组成的民主党中担任领导,以期获得从北部辉格党那里得不到的好处。......
2023-12-02

在接受美国博伊斯州立大学名誉博士学位仪式上的致辞今天,我十分荣幸地接受博伊斯州立大学授予我的人文科学名誉博士学位,这是对我在残疾人工作领域所取得的成就的肯定,对我在人道主义思想研究与实践方面的学养给予的高度评价。上述种种丑恶现象,是对人类尊严与权利最大的践踏。我衷心祝愿中美两国人民的友谊不断发展,祝愿世界上所有人民生活更加安康富足,祝博伊斯州立大学不断发展,祝在座的所有朋友生活幸福。......
2024-09-05

在R 软件中,有个MASS包,其中有一个caith数据集,是关于眼睛颜色和头发颜色的数据.(1)查看caith数据集的信息>library(MASS)>caith结果如下:从以上结果可以看出,caith数据集中眼睛颜色:blue,light,medium 和dark;头发颜色:fair,red,medium,dark和black.(2)进行χ2 检验——考察行变量和列变量是否独立>chisq.te......
2023-11-18

简单地说,摩尔主要是对日常语言进行分析,并且主张捍卫“常识”。以上三个例子有一个共同的特征,这就是违反一般的常识,而摩尔的反驳恰恰是利用我们的常识,并且捍卫我们的常识。......
2024-01-22

对于工商人户来说,承应地方官府的差务,行业、范围和负担比重,都是较为固定的。这些衙署的运作和修葺,需要民众,特别是工商人户承担差役负担。丛集在衙署中数量惊人的衙役,更要从工商人户的应值差承中获得谋生之资和非分之利。[69]事在四川,重庆工商户承担的差务自然特别繁重。......
2023-10-16

审美教育哲学把音乐教育定义为感觉教育,但与我国传统音乐美学有所不同,审美教育哲学理论将情感扩大到了感觉尺度上,并将情感和感觉定义为局部和总体的关系。......
2023-07-04
相关推荐