首页理论教育多元统计分析：R实验中的数据变换方法

多元统计分析：R实验中的数据变换方法

2023-11-18 理论教育版权反馈

【摘要】：，n）．记则其中，1p＝（1，1，…，pn·）表示对角线元素为p1·，p2·，…，pn· 的对角矩阵．因此，经过变换后所得到的新数据矩阵B，可以看成是由对应矩阵P 经过中心化和标准化后得到的矩阵．设用于检验行与列是否不相关的χ2 统计量为其中，表示第（i，j）单元在检验行与列两个属性变量否不相关时对总χ2 统计量的贡献，有其中，χ2＝＝T[tr]＝T[tr]＝T[tr]，tr表示方阵SQ 的迹．

设有n 个样品，每个样品观测p 个指标，原始数据阵为

为了消除量纲或数量级的差异，经常对变量进行标准化处理，如标准化变换、极差标准化变换等，这些变换对变量和样品是不对称的．这种不对称性是导致变量和样品之间关系复杂化的主要原因．在对应分析中，采用数据的变换方法即可克服这种不对称性（假设所有数据aij＞0，否则对所有数据同加一适当常数，便会满足以上要求）．数据变换方法的具体步骤如下：

（1）化数据矩阵为规格化的“概率”矩阵P，令

其中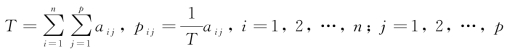， pagenumber_ebook=223,pagenumber_book=214 ．

可以看出0≤pij ≤1，且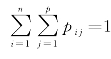 pagenumber_ebook=223,pagenumber_book=214 ．因而pij 可理解为数据aij 出现的“概率”，并称P 为对应矩阵．

记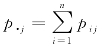 pagenumber_ebook=223,pagenumber_book=214 可理解为第j 个变量的边缘概率（j＝1，2，…，p）；pi·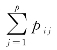＝可理解为第i个样品的边缘概率（i＝1，2，…，n）．

记

则

其中，1p＝（1，1，…，1）T 为元素全为1的p 维常数向量．

（2）进行数据的对应变换，令

B＝(bij)n×p,

其中

这里，．(www.chuimin.cn)

式（11．2．3）就是我们从同时研究R 型和Q 型因子分析的角度导出的数据对应变换公式．

（3）计算有关矩阵，记

SR＝BT B,SQ＝BBT,

考虑R 型因子分析时应用SR，考虑Q 型因子分析时应用SQ．

如果把所研究的p 个变量看成一个属性变量的p 个类目，而把n 个样品看成另一个属性变量的n 个类目，这时原始数据阵A 就可以看成一张由观测得到的频数表或计数表．首先由双向频数表A 矩阵得到对应矩阵

设n＞p，且rank（P）＝p．以下从代数学角度由对应矩阵P 来导出数据对应变换的公式．

引理11．2．1 数据标准化矩阵

其中，Dr＝diag（p1·，p2·，…，pn·），Dc＝diag（p·1，p·2，…，p·p），这里diag（p1·，p2·，…，pn·）表示对角线元素为p1·，p2·，…，pn· 的对角矩阵．

因此，经过变换后所得到的新数据矩阵B，可以看成是由对应矩阵P 经过中心化和标准化后得到的矩阵．

设用于检验行与列是否不相关的χ2 统计量为

其中，表示第（i，j）单元在检验行与列两个属性变量否不相关时对总χ2 统计量的贡献，有

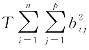其中，χ2＝ pagenumber_ebook=225,pagenumber_book=216 ＝T[tr（BT B）]＝T[tr（SR）]＝T[tr（SQ）]，tr（SQ）表示方阵SQ 的迹．