首页理论教育使用R进行实验：分析ability.cov数据集的因子

使用R进行实验：分析ability.cov数据集的因子

2023-11-18 理论教育版权反馈

【摘要】：ability．cov数据集是R 软件自带的数据集，以下对该数据集进行因子分析．（1）查看ability．cov数据集中的信息ability．cov数据集提供了Ability and Intelligence Tests（能力和智力测试）中，112个人参加的六个测试指标general（普通），picture（画图），blocks（积木），maze（迷津），reading（阅读），vocab（词汇）

ability．cov数据集是R 软件自带的数据集，以下对该数据集进行因子分析．

（1）查看ability．cov数据集中的信息

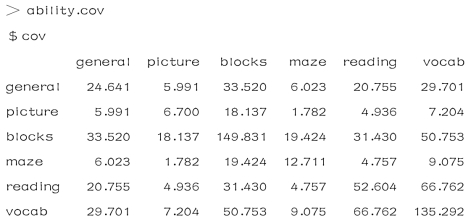
pagenumber_ebook=202,pagenumber_book=193

ability．cov数据集提供了Ability and Intelligence Tests（能力和智力测试）中，112个人参加的六个测试指标general（普通），picture（画图），blocks（积木），maze（迷津），reading（阅读），vocab（词汇）的协方差矩阵．

（2）求相关系数矩阵

以下用“cov2cor（）”函数将ability．cov（协方差矩阵）转化为相关系数矩阵，其代码和结果如下：

pagenumber_ebook=202,pagenumber_book=193

（3）判断需提取的公共因子数

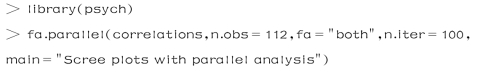
pagenumber_ebook=202,pagenumber_book=193

结果如图10-1所示．

以上代码中使用fa＝“both”，可以使图10-1展示主成分分析和因子分析的结果，我们可以借助图10-1来判断提取公共因子数．

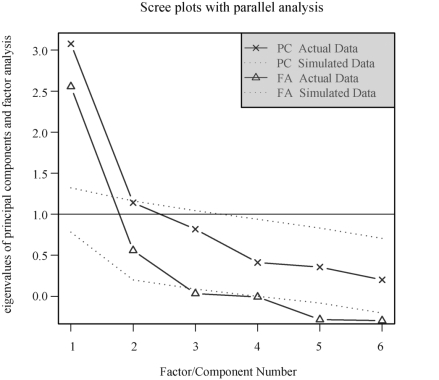
pagenumber_ebook=203,pagenumber_book=194

图10-1　判断提取公共因子数

如图10-1所示，通过实际数据（Actual Data）和模拟数据（Simulated Data）的可视化结果，提取2个公共因子比较合理．

（4）提取公共因子——未旋转（rotate＝none）

用“fa（）”函数（其调用格式附后）提取公共因子，其代码和结果如下：

pagenumber_ebook=203,pagenumber_book=194

pagenumber_ebook=204,pagenumber_book=195

从以上结果可以看到，两个因子解释了六个测试指标60%的方差．此时因子载荷矩阵的意义不好解释，这时可以考虑使用因子旋转，它将有助于因子的解释．

附：“fa（）”函数的调用格式如下：

fa(r,nfactors＝,n．obs＝,rotate＝,scores＝,fm＝)

其中，r是相关系数矩阵或者原始数据矩阵；nfactors设定提取的因子数（默认为1）；n．obs是观测数（输入相关系数矩阵时需要填写）；rotate设定旋转的方法（默认变异系数最小法）；scores设定是否计算因子得分（默认不计算）；fm 设定因子化方法（默认极小残差法）．

提取公共因子的方法很多，包括极大似然法（ml）、主迭代法（pa）、加权最小二乘法（wls）、广义加权最小二乘法（gls）和极小残差法（minres）．在上面的代码中，使用了主迭代法（fm＝“pa”）提取未旋转的公共因子．

（5）提取公共因子——正交旋转

结合上面（4）的结果，可以看到（未旋转时），2个因子解释了6个测量指标的60%的变异，解释的效果并不好，且因子载荷矩阵的意义并不太好解释．因此可以考虑进行因子旋转，使因子有一个更好的解释．

正交旋转的代码和结果如下：

pagenumber_ebook=205,pagenumber_book=196

pagenumber_ebook=206,pagenumber_book=197

（6）正交旋转效果图

使用“factor．plot（）”或“fa．diagram（）”函数，可以绘制正交或斜交结果的图形．画正交旋转效果图，代码和结果如下：

＞factor．plot(fa．varimax,labels＝rownames(fa．varimax＄loadings))(www.chuimin.cn)

＞fa．diagram(fa．varimax,simple＝TRUE)

正交旋转结果如图10-2和图10-3所示．

pagenumber_ebook=206,pagenumber_book=197

图10-2　正交旋转效果图-1

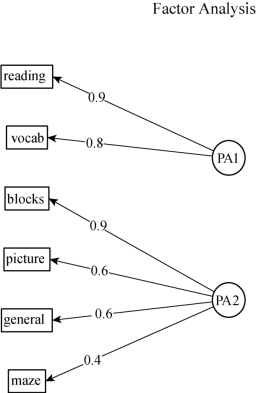
pagenumber_ebook=206,pagenumber_book=197

图10-3　正交旋转效果图-2

从图10-2和图10-3，我们看到：reading（阅读）与vocab（词汇）在第一因子上载荷较大；picture（画图），blocks（积木），maze（迷津）在第二个因子上载荷较大；general（普通）在两个因子上的载荷比较平均．这表明存在一个“语言”智力因子和一个“非语言”智力因子．

（7）提取公共因子——斜交旋转

使用正交旋转将人为地强制两个因子不相关．如果想允许两个因子相关该如何呢？这时可用斜交旋转法，代码和结果如下：

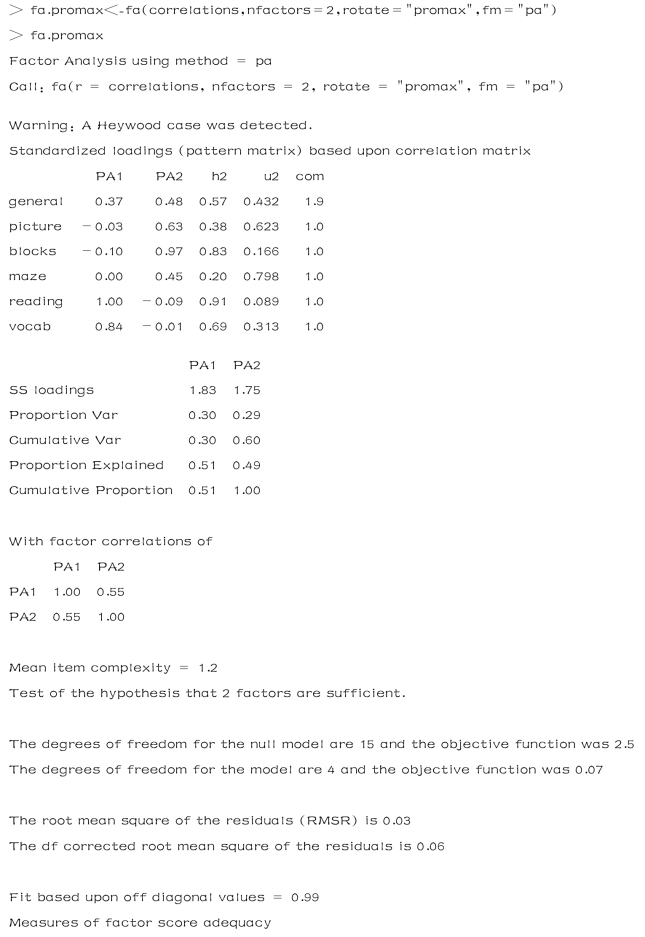
pagenumber_ebook=207,pagenumber_book=198

pagenumber_ebook=208,pagenumber_book=199

根据以上结果，我们可以看出正交旋转和斜交旋转的不同之处．对于正交旋转，因子分析的重点在于因子结构矩阵（变量与因子的相关系数），而对于斜交旋转，因子分析会考虑三个矩阵：因子结构矩阵、因子模式矩阵和因子关联矩阵．

因子模式矩阵即标准化的回归系数矩阵，它列出了因子的预测变量的权重；因子关联矩阵即因子相关系数矩阵；因子结构矩阵（或称因子载荷阵）．

在上面的结果中，PA1和PA2栏中的值组成了因子模式矩阵．它们是标准化的回归系数，而不是相关系数．因子关联矩阵显示两个因子的相关系数为0．55，相关性很大．如果因子间的关联性很低，我们可能需要重新使用正交旋转来简化问题．

因子结构矩阵（或称因子载荷矩阵）没有被列出来，但我们可以使用公式F＝P·Phi得到它，其中F是因子载荷阵，P是因子模式矩阵，Phi是因子关联矩阵．下面的函数即可进行该乘法运算：

pagenumber_ebook=208,pagenumber_book=199

现在我们可以看到变量与因子间的相关系数．将它们与正交旋转所得因子载荷阵相比，我们会发现该载荷阵列的噪音比较大，这是因为之前我们允许潜在因子相关．虽然斜交旋转方法更为复杂，但因子的解释更好一些．

（8）斜交效果图

使用“factor．plot（）”或“fa．diagram（）”函数，可以绘制正交或斜交结果的图形．画斜交效果，其代码和结果如下：

＞factor．plot(fa．promax,labels＝rownames(fa．promax＄loadings))

＞fa．diagram(fa．promax,simple＝TRUE)

斜交效果图如图10-4和图10-5所示．

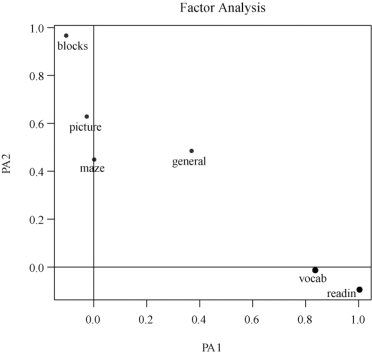
pagenumber_ebook=209,pagenumber_book=200

图10-4　斜交效果图-1

pagenumber_ebook=209,pagenumber_book=200

图10-5　斜交效果图-2

从图10-5（或斜交旋转的因子载荷矩阵）我们可以看到：因子1支配的指标有reading（阅读），vocab（词汇），代表的是“语言智力”因子；因子2支配的指标有general（常识），picture（画图），blocks（积木），maze（迷津），代表的是“非语言智力”因子．

（9）通过两个因子的斜交旋转可获得因子得分的权重

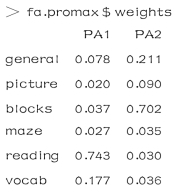
pagenumber_ebook=209,pagenumber_book=200

与可精确计算的主成分得分不同，因子得分只是估计得到的．