实际上主成分分析可以说是因子分析（factor analysis）的一个特例．主成分分析从原理上是寻找椭球的所有主轴．因此，原先有几个变量就有几个主成分．而因子分析是事先确定要找几个成分（component），也称为因子（factor）（从数学模型本身来说是事先确定因子个数，但统计软件是事先确定因子个数，或者把符合某些标准的因子都选入）．变量和因子个数的不一致使得不仅在数学模型上，而且在计算方法上......
2023-11-18
因子旋转方法及其应用
【摘要】：建立因子分析模型的目的不仅仅要找出公共因子以及对变量进行分组，更重要的要知道每个公共因子的意义，以便进行进一步的分析，如果每个公共因子的含义不清，则不便于进行实际背景的解释．由于因子载荷阵是不唯一的，所以应该对因子载荷阵进行旋转．目的是使因子载荷阵的结构简化，使载荷矩阵每列或行的元素平方值向0和1两级分化．有三种主要的正交旋转法：方差最大法、四次方最大法和等量最大法．（1）方差最大法方差最大法从简
建立因子分析模型的目的不仅仅要找出公共因子以及对变量进行分组，更重要的要知道每个公共因子的意义，以便进行进一步的分析，如果每个公共因子的含义不清，则不便于进行实际背景的解释．由于因子载荷阵是不唯一的，所以应该对因子载荷阵进行旋转．目的是使因子载荷阵的结构简化，使载荷矩阵每列或行的元素平方值向0和1两级分化．有三种主要的正交旋转法：方差最大法、四次方最大法和等量最大法．
（1）方差最大法
方差最大法从简化因子载荷矩阵的每一列出发，使和每个因子有关的载荷的平方的方差最大．当只有少数几个变量在某个因子上有较高的载荷时，对因子的解释最简单．方差最大的直观意义是希望通过因子旋转后，使每个因子上的载荷尽量拉开距离，一部分的载荷趋于±1，另一部分趋于0．
（2）四次方最大法
四次方最大旋转是从简化载荷矩阵的行出发，通过旋转初始因子，使每个变量只在一个因子上有较高的载荷，而在其他的因子上有尽可能低的载荷．如果每个变量只在一个因子上有非零的载荷，这时的因子解释是最简单的．四次方最大法通过使因子载荷矩阵中每一行的因子载荷平方的方差达到最大．
（3）等量最大法
等量最大法把四次方最大法和方差最大法结合起来，求它们的加权平均最大．(www.chuimin.cn)
对两个因子的载荷矩阵
Λ＝(aij)p×2,i＝1,2,…,p;j＝1,2．
取正交矩阵
这是逆时针旋转，如果作正时针旋转，只需将矩阵B 的次对角线上的两个元素对调即可．记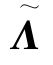
＝ΛB 为旋转因子的载荷矩阵，此时模型由X－μ＝ΛF＋ε 变为
同时公因子F 也随之变为BT F，现在希望通过旋转，使因子的含义更加明确．
当公因子数m＞2时，可以考虑不同的两个因子的旋转，从m 个因子中每次选取两个旋转，共有m（m－1）/2种选择，这样共有m（m－1）/2次旋转，做完这m（m－1）/2次旋转就完成了一个循环，然后可以重新开始第二次循环，直到每个因子的含义都比较明确为止．
有关应用多元统计分析：基于R的实验的文章
- 详细阅读
-
定位特征及其应用方法详细阅读
定位特征是为构造新特征提供定位功能的，它包括工作平面、工作轴、工作点。可以将工作平面作为新的草图平面，也可以将它作为特征的限位面以及装配时的辅助定位面。单击“模型”选项卡中的“定位特征”选项，如图5-37所示，即可以生成工作平面等。图5-36系统默认的定位特征图5-37“定位特征”工具条1.工作平面的创建创建工作平面的方法就是根据几何知识确定平面的方法。......
2023-06-28
-
实践美学方法及其应用详细阅读
从数量众多的艺术美学理论成果，特别是教材编写出版情况来看，学术界对西方传统美学的研究与应用较为普遍、清晰，而对马克思主义美学中国化的理论研究及其应用，显得目标不明、思路不清。可以说，刘纲纪运用中国化的马克思主义美学理论研究并阐述中国艺术美学理论，在谢赫画论研究上达到了较为圆熟的境界，是马克思主义美学中国化及其在艺术美学领域成熟应用的杰出范例。......
2023-08-22
-
人格测量方法及其应用详细阅读
人格测量的主要方法有自陈量表法和投射测验法。自陈量表法自陈量表法是让被试按自己的意见，对自己的人格特质进行评价的一种方法。自陈量表通常也称为人格量表。用自陈量表法编制的人格量表，在我国常见的有明尼苏达多项人格测验量表、爱德华个人兴趣量表、卡特尔系列人格特征量表和艾森克人格类型量表等。明尼苏达多项人格测验包括10个临床量表。......
2023-11-06
-
饲料小动物的温度因子及其影响详细阅读
（一）温度因子1．温度影响蚯蚓的体温、活动能力及生存蚯蚓属于变温动物，其体温随外界环境温度的变化而变化，即外界温度高体温增高，外界温度低体温降低。如环毛蚓的致死高温为37℃以上，赤子爱胜蚓和威廉环毛蚓的致死高温为39℃以上。赤子爱胜蚓在8℃以下就完全停止产卵。实践证明，赤子爱胜蚓的最佳繁殖温度为20～25℃，在8～25℃，其卵包的产量与温度高低呈正相关。......
2024-01-18
-
AutoCAD2012应用教程：旋转详细阅读
调用命令方式·下拉菜单：修改→旋转。功能将选择的对象旋转指定的角度。将图6-33中的正方形绕矩形中心点逆时针旋转160°。命令：_rotateUCS当前的正角方向：ANGDIR=逆时针 ANGBASE=0选择对象：指定对角点：找到4个 选择对象：↙ 指定基点： 指定旋转角度，或[复制/参照]<0>：160↙ 旋转后的图形如图6-35所示。单击“修改”工具栏中的“旋转”按钮，命令行提示如下。图6-36 例题6-9图例图6-37 进行旋转操作后的效果......
2023-10-21
-
人体运动观测方法及其应用详细阅读
观测人体运动要确定观测对象及观测坐标系。在人体运动的研究中，最常用的是直角坐标系。常用的直角坐标系有三种：一维坐标系：直线运动，沿着一个方向运动，如一百米跑、游泳等。视频跟踪法是应用视频对人体的运动进行跟踪、捕捉和分析。图3-18摄影观察法人体运动属于非刚体运动的范畴，具有高度的非线性特点。......
2023-06-21
-
线段的旋转技巧与方法详细阅读
图3-56线段的旋转由图3-56中可以看出，△aob和△a1ob1中，ao=a1o，bo=b1o，∠aob=∠θ-∠boa1=∠a1ob1，因此△aob≌△a1ob1，ab=a1b1。这就是说，当线段绕铅垂线旋转时，水平投影的长度不变。由直线的旋转可解决以下三个基本作图问题。由上述可知，一次旋转成为投影面平行线，再次旋转成为投影面垂直线。例3-27使一般位置直线AB变成铅垂线。图3-60平面的旋转......
2023-06-28
相关推荐