在实验2．3．2中曾对iris数据集进行描述和展示，在实验2．3．4中曾对iris数据集进行可视化．以下将对iris数据集进行进行聚类分析．根据实验2．3．4，我们只知道数据集内有三个品种鸢尾花而不知道每朵花的真正分类，只能凭借花萼及花瓣的长度和宽度分类．以下对鸢尾花iris数据集进行聚类分析，代码如下：＞data(iris);attach(iris)＞iris．hc1＜-hclust(dist(......
2023-11-18
基于R的USJudgeRatings数据集主成分分析
【摘要】：USJudgeRatings数据集（R 自带），该数据集来自psych包，需加载以及调用psych包．（1）首先查看USJudgeRatings数据集的信息该数据集包含了律师对美国高等法院法官的评分，数据包含43个观测值，12个变量．12个变量如下：CONT：律师与法官的接触次数；INTG：法官正直程度；DMNR：风度；DILG：勤勉度；CFMG：案例流程管理水平；DECI：决策效率；PREP：审
USJudgeRatings数据集（R 自带），该数据集来自psych包，需加载以及调用psych包．
（1）首先查看USJudgeRatings数据集的信息
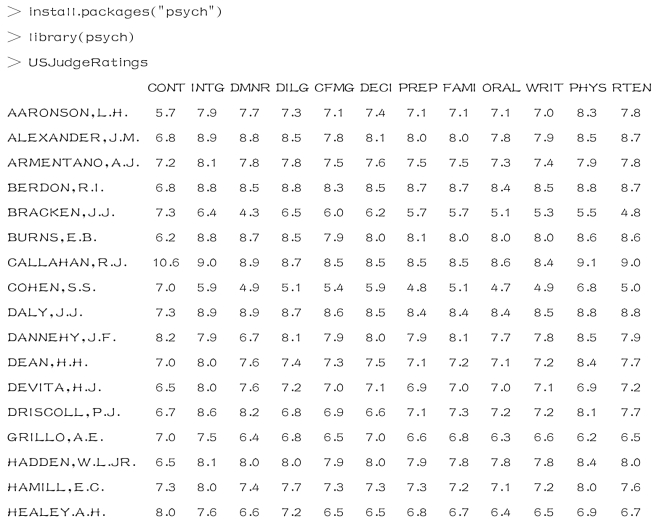
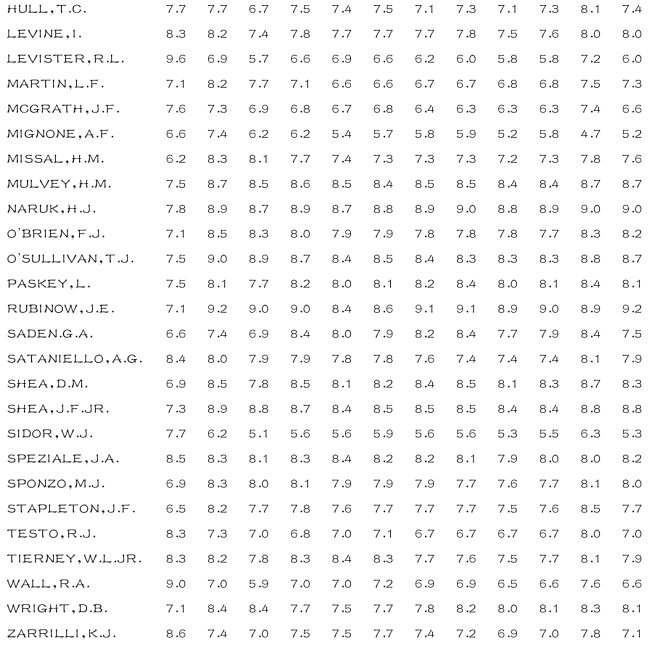
该数据集包含了律师对美国高等法院法官的评分，数据包含43个观测值，12个变量．
12个变量如下：
CONT：律师与法官的接触次数；
INTG：法官正直程度；
DMNR：风度；
DILG：勤勉度；
CFMG：案例流程管理水平；
PREP：审理前的准备工作；
FAMI：对法律的熟稔程度；
ORAL：口头裁决的可靠度；
WRIT：书面裁决的可靠度；
PHYS：体能；
RTEN：是否值得保留．
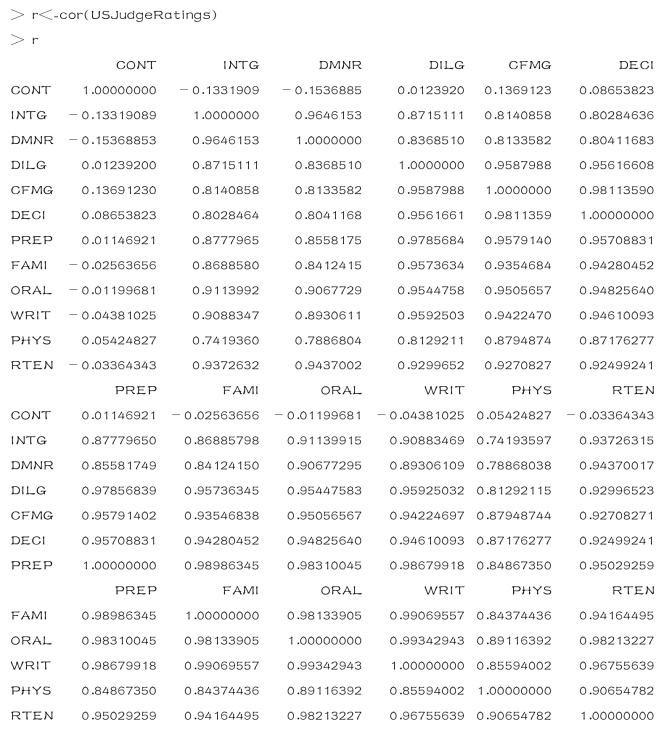
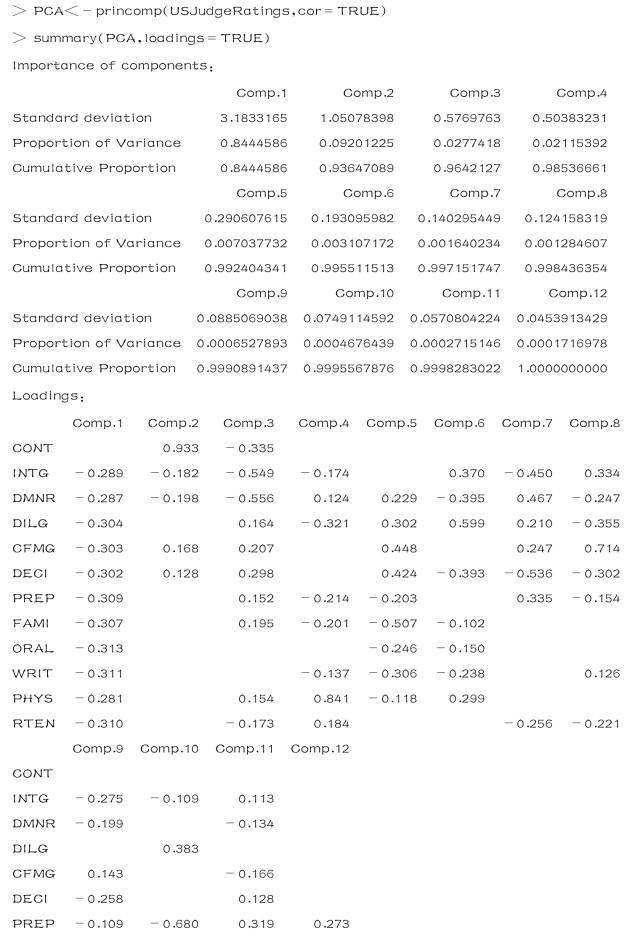
（3）进行主成分分析
(www.chuimin.cn)
Standard deviation 为主成分的标准差，proportion of variance 为贡献率，cumulative of proportion为累计贡献率．从以上计算结果中可以得出每个成分的贡献率、累计贡献率：对于成分一的贡献率为0．844 458 6；成分二的贡献率为0．092 012 25，前两个成分的累计贡献率达0．936 470 89，因此可以选取两个主成分．
（4）画碎石图
＞fa．parallel(USJudge Ratings,fa＝＂pc＂,n．iter＝100,show．legend＝FALSE,main＝＂screeplot＂)
结果如图9-2所示．
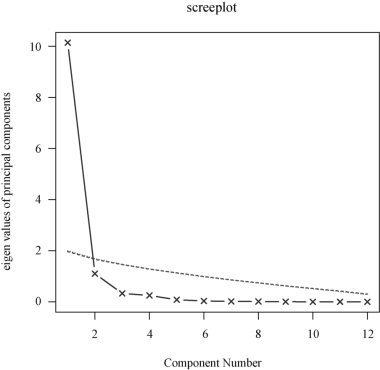
图9-2 碎石图
从图9-2（碎石图）也可以看出，选取两个主成分比较合理．
（5）计算特征值以及特征向量
可以得到特征值为10．133 5，1．104 1，0．332 9，0．253 8，0．084 4，0．037 3，0．019 7，0．015 4，0．007 8，0．005 6，0．003 3，0．002 1．
综合前面所选取的主成分个数，可以得出两个主成分，分别为：
（6）计算主成分得分及主成分排名
从以上排名结果可以看出：RUBINOW，J．E．排名第一；NARUK，H．J．排名第二；BERDON，R．I．排名第三；COHEN，S．S；遗憾排名最后．
由于判断法官综合能力的变量有限仅为12个变量，排名结果可能不能完全地体现各位法官的综合能力，因此排名可能并非全面，结果仅供参考．
有关应用多元统计分析：基于R的实验的文章
- 详细阅读
-
基于R的实验：Harman74数据集的因子分详细阅读
Harman74．cor数据集是R 软件自带的数据集，以下对该数据集进行因子分析．（1）查看Harman74数据集中（前面）部分信息Harman74．cor数据集，包含了对芝加哥郊区145名七年级和八年级儿童进行的24 项心理测试指标的相关系数矩阵．其中的24 项心理测试指标包括：VisualPerception，Cubes，PaperFormBoard，Flags，GeneralInformat......
2023-11-18
-
主成分分析与因子分析及其R应用详细阅读
实际上主成分分析可以说是因子分析（factor analysis）的一个特例．主成分分析从原理上是寻找椭球的所有主轴．因此，原先有几个变量就有几个主成分．而因子分析是事先确定要找几个成分（component），也称为因子（factor）（从数学模型本身来说是事先确定因子个数，但统计软件是事先确定因子个数，或者把符合某些标准的因子都选入）．变量和因子个数的不一致使得不仅在数学模型上，而且在计算方法上......
2023-11-18
-
基于R的多元统计分析：mtcars数据集可视详细阅读
在实验2．3．1中，我们对mtcars数据集（R 自带数据集）进行了展示和描述，以下对该数据集进行可视化．（1）汽车每加仑英里数直方图＞hist(mtcars＄mpg,breaks＝10)结果如图2-1所示．（2）按汽缸数划分的各车型车重的核密度图＞par(lwd＝2)＞library(sm)＞cyl．f＜－factor(mtcars＄cyl,levels＝c(4,6,8),labels＝c(＂4......
2023-11-18
-
UScereal数据集方差分析：基于R的多元详细阅读
用MASS包中的UScereal数据集，我们研究美国谷物中的卡路里、脂肪和糖含量是否会因为储存架位置的不同而发生变化．其中1代表底层货架，2代表中层货架，3代表顶层货架．卡路里（calories）、脂肪（fat）和糖（sugars）含量是因变量，货架是3水平（1，2，3）的自变量．（1）单因素多元方差分析在以上代码中，“cbind（ ）”函数将三个变量（calories，fat，sugars）合并......
2023-11-18
-
数据降维与主成分分析详细阅读
为了说明什么是数据的主成分，先从数据降维说起。一般来讲，n维空间中的n个点一定能在一个n－1维子空间中分析。在上一段中，我们可以认为数据降维后并没有丢弃任何东西，因为这些数据在平面以外的第三个维度的分量都为0。主成分分析的思想:将n维特征映射到k维上(k＜n)，这k维是全新的正交特征。这k维特征称为主成分，是重新构造出来的k维特征，而不是简单地从n维特征中去除其余n－k维特征。......
2023-06-21
-
多元回归分析：R语言中stackloss数据详细阅读
在实验4．4．1中曾对R 自带的stackloss数据集进行了逐步回归，现在我们在实验4．4．1的基础上进行回归诊断．（1）画回归诊断图＞opar＜－par(mfrow＝c(2,2))＞plot(lm．step,1：4)＞par(opar)结果如图4-2所示．图4-2回归诊断图分析4张回归诊断图（图4-2）．第1张是残差图，得到的残差图呈喇叭口形状，属于异方差情况（这样的数据需要作Box-Cox......
2023-11-18
-
基于R的实验stackloss数据集逐步回归详细阅读
对R 自带的stackloss数据集进行逐步回归．（1）首先显示stackloss数据集的信息其中，变量为stack．loss（氨气损失百分比），Air．Flow（空气流量），Water．Temp（水温），Acid．Conc．（硝酸浓度）．（2）计算变量间的相关性——相关系数＞cor(stackloss)结果如下：（3）散布图矩阵＞library(car)＞scatterplotMatrix(st......
2023-11-18
相关推荐