主成分分析法的主要优点包括:①可消除评估指标之间的相关影响。对于其他评估方法，由于难以消除评估指标间的相关影响，所以选择指标时要花费较多精力，而主成分分析法可以消除这种相关影响，所以在指标选择上相对容易些。对纽约交通事故进行主成分分析，从分析结果可以看出，KMO取样适宜性数量为0.491，巴特利特球形度检验的近似卡方值为1533.013，自由度为36，显著性小于0.001。表4.2旋转后的成分矩阵......
2023-06-15
首批沿海开放城市的主成分分析成果
【摘要】：2009年14个首批沿海开放城市（大连市、秦皇岛市、天津市、烟台市、青岛市、连云港市、南通市、上海市、宁波市、温州市、福州市、广州市、湛江市、北海市）实现地区生产总值达到60 003．47亿元，全国国内生产总值为335 353．00亿元，首批沿海开放城市地区生产总值占全国的17．9%，大大高出了人口占全国的比重（7．1%）．在遵循合理性、代表性、系统性、可比性、可操作性及可获得性的原则下，选取了能
2009年14个首批沿海开放城市（大连市、秦皇岛市、天津市、烟台市、青岛市、连云港市、南通市、上海市、宁波市、温州市、福州市、广州市、湛江市、北海市）实现地区生产总值达到60 003．47亿元，全国国内生产总值为335 353．00亿元，首批沿海开放城市地区生产总值占全国的17．9%，大大高出了人口占全国的比重（7．1%）．
在遵循合理性、代表性、系统性、可比性、可操作性及可获得性的原则下，选取了能反映城市综合经济实力的11项统计指标，建立起相应的统计指标体系，应用主成分分析的方法对各城市综合实力进行评价．选取反映经济情况的11项主要指标：地区生产总值x1，人均地区生产总值x2，社会消费品零售总额x3，地方财政一般预算收入x4，工业总产值x5，城镇固定资产投资x6，农村居民人均纯收入x7，进出口总额x8，实际外商直接投资x9，农林牧渔业总产值x10，城镇居民人均可支配收入x11．14个首批沿海开放城市各评价指标数据见表9-1．
表9-1 14个首批沿海开放城市各评价指标数据
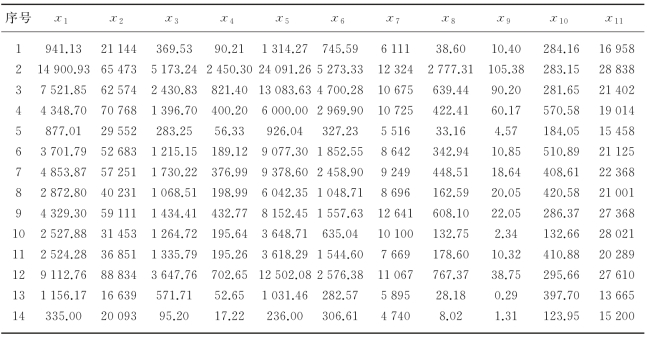
说明：在上表中序号1—14分别代表：连云港，上海，天津，大连，秦皇岛，烟台，青岛，南通，宁波，温州，福州，广州，湛江，北海．
＞x1＝c(941．13,14900．93,7521．85,4348．7,877．01,3701．79,4853．87,2872．8,4329．3,2527．88,2524．28,9112．76,1156．17,335)
＞x2＝c(21144,65473,62574,70768,29552,52683,57251,40231,59111,31453,36851,88834,16639,20093)
＞x3＝c(369．53,5173．24,2430．83,1396．7,283．25,1215．15,1730．22,1068．51,1434．41,1264．72,1335．79,3647．76,571．71,95．2)
＞x4＝c(90．21,2450．3,821．4,400．2,56．33,189．12,376．99,198．99,432．77,195．64,195．26,702．65,52．65,17．22)
＞x5＝c(1314．27,24091．26,13083．63,6000,926．04,9077．3,9378．6,6042．35,8152．45,3648．71,3618．29,12502．08,1031．46,236)
＞x6＝c(745．59,5273．33,4700．28,2969．9,327．23,1852．55,2458．9,1048．71,1557．63,635．04,1544．6,2576．38,282．57,306．61)
＞x7＝c(6111,12324,10675,10725,5516,8642,9249,8696,12641,10100,7669,11067,5895,4740)
＞x8＝c(38．6,2777．31,639．44,422．41,33．16,342．94,448．51,162．59,608．1,132．75,178．6,767．37,28．18,8．02)
＞x9＝c(10．4,105．38,90．2,60．17,4．57,10．85,18．64,20．05,22．05,2．34,10．32,38．75,0．29,1．31)
＞x10＝c(284．16,283．15,281．65,570．58,184．05,510．89,408．61,420．58,286．37,132．66,410．88,295．66,397．7,123．95)
＞x11＝c(16958,28838,21402,19014,15458,21125,22368,21001,27368,28021,20289,27610,13665,15200)
＞X＝data．frame(x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11)
＞cor(X)
结果如下：
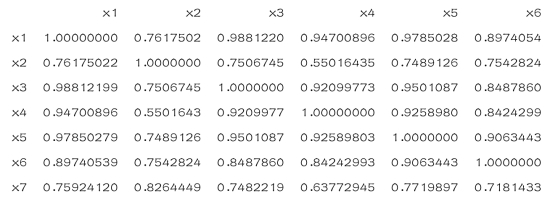
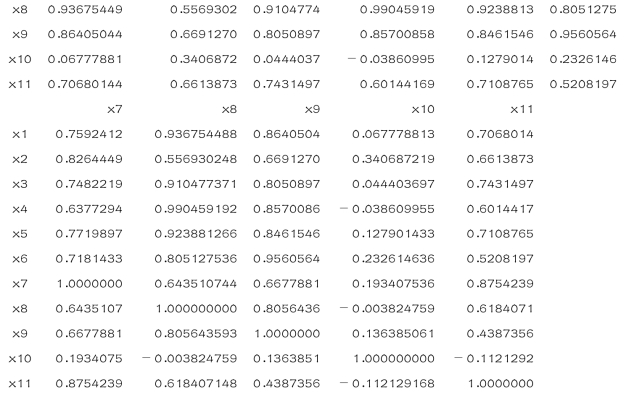
（2）求特征值、贡献率(www.chuimin.cn)
以上有关结果见表9-2．
表9-2 特征值、贡献率和累计贡献率
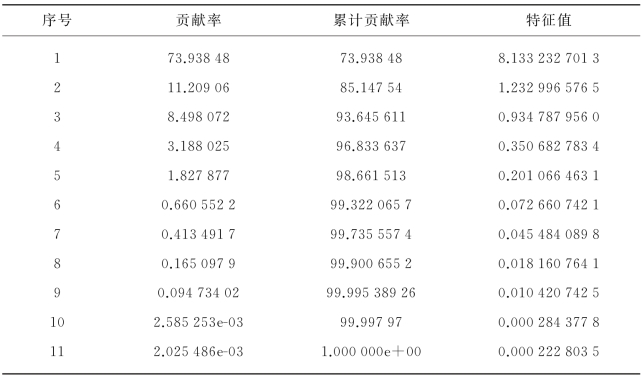
从表9-2可知，前两个特征值的累计贡献率就达到了85%以上．
（3）画碎石图
＞PCA＝princomp(X,cor＝T)
＞screeplot(PCA,type＝ˈlinesˈ)
结果如图9-1所示．
从图9-1中也可以看出，提取前2个主成分是比较合适的．
（4）计算综合得分并进行排名
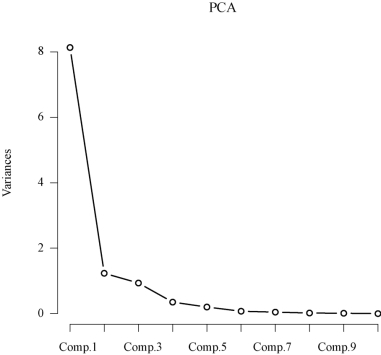
图9-1 碎石图
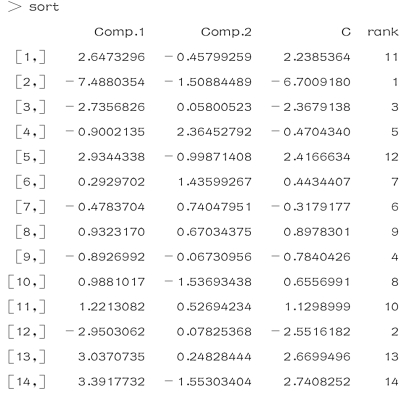
根据上面的结果，14个首批沿海开放城市的主成分得分及排名见表9-3．
表9-3 14个首批沿海开放城市的主成分得分及排名
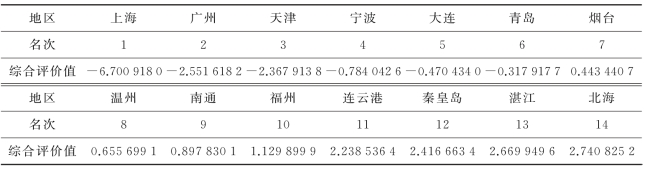
需要说明，由于以上排名仅根据反映经济情况的11项主要指标进行，可能并非全面，其结果仅供参考．
有关应用多元统计分析：基于R的实验的文章
- 详细阅读
-
基于R的USJudgeRatings数据集主详细阅读
USJudgeRatings数据集（R 自带），该数据集来自psych包，需加载以及调用psych包．（1）首先查看USJudgeRatings数据集的信息该数据集包含了律师对美国高等法院法官的评分，数据包含43个观测值，12个变量．12个变量如下：CONT：律师与法官的接触次数；INTG：法官正直程度；DMNR：风度；DILG：勤勉度；CFMG：案例流程管理水平；DECI：决策效率；PREP：审......
2023-11-18
-
数据降维与主成分分析详细阅读
为了说明什么是数据的主成分，先从数据降维说起。一般来讲，n维空间中的n个点一定能在一个n－1维子空间中分析。在上一段中，我们可以认为数据降维后并没有丢弃任何东西，因为这些数据在平面以外的第三个维度的分量都为0。主成分分析的思想:将n维特征映射到k维上(k＜n)，这k维是全新的正交特征。这k维特征称为主成分，是重新构造出来的k维特征，而不是简单地从n维特征中去除其余n－k维特征。......
2023-06-21
-
主成分分析与因子分析及其R应用详细阅读
实际上主成分分析可以说是因子分析（factor analysis）的一个特例．主成分分析从原理上是寻找椭球的所有主轴．因此，原先有几个变量就有几个主成分．而因子分析是事先确定要找几个成分（component），也称为因子（factor）（从数学模型本身来说是事先确定因子个数，但统计软件是事先确定因子个数，或者把符合某些标准的因子都选入）．变量和因子个数的不一致使得不仅在数学模型上，而且在计算方法上......
2023-11-18
-
主成分分析：基本思想及方法详细阅读
，xp 表示p 门课程，c1，c2，…＋cp xp．我们希望选择适当的权重能更好地区分学生的成绩．每个学生都对应一个这样的综合成绩，记为s1，s2，…，sn．如果这些值很分散，表明区分得好，就是说，需要寻找这样的加权，能使s1，s2，…，sn 尽可能的分散，下面来看它的统计定义．设X1，X2，…，Xp 表示以x1，x2，…，xp 为样本观测值的随机变量，如果能找到c1，c2，…，c1p）使得Var的值达到最大；（c21，c22，…，c3p）同时垂直于（c11，c12，…......
2023-11-18
-
应用多元统计分析：主成分分析的实例详细阅读
那就是这些被选的主成分所代表的主轴的长度之和占了主轴长度总和的大部分．有些文献建议，所选的主轴总长度占所有主轴长度之和的大约80%即可．其实，这只是一个大体的说法；具体选几个，要看实际情况而定．但如果所有涉及的变量都不那么相关，就很难降维．不相关的变量就只有自己代表自己了．......
2023-11-18
-
主成分分析揭示干旱胁迫对植物生物量详细阅读
对4 种植物不同器官的生物量、δ13C 值组成及N、P、K 营养元素含量进行主成分分析，结果如表6-5 所示，最终得到3 个特征值大于1的主成分，累计百分比为78.95%，可以反映原始指标的大部分信息。表6-5不同主成分的特征值和累积贡献值 Table 6-5Principal component variance analysis表6-6主成分载荷矩阵 Table 6-6Principal Component Load Matrix图6-5干旱胁迫对4 种植物生物量、δ13C 值及营养元素影响的主成分分析 Fig.6-5The principal component analysis of the effects of drought stress on biomass， δ 13C value and nutrient elements of 4 plant species......
2023-11-04
-
因子分析与主成分分析：深入理解和应用详细阅读
主成分分析也称主分量分析，旨在利用降维的思想，把多指标转化为少数几个综合指标。当然，这种情况也可以使用因子分析做到，所以它们的区分不是绝对的。可以说，因子分析是主成分分析的推广，也是一种把多个变量化为少数几个综合变量的多变量分析方法，其目的是用有限个不可观测的隐变量来解释原始变量之间的相关关系。因子分析主要用于：减少分析变量个数；通过对变量间相关关系探测，将原始变量进行分类。......
2023-08-23
相关推荐