首页理论教育应用多元统计分析：判别准则与函数

应用多元统计分析：判别准则与函数

2023-11-18 理论教育版权反馈

【摘要】：以下我们来讨论两个总体的距离判别，分别讨论两个总体协方差矩阵相同和不同的情况．设总体X1 和X2 的均值向量分别为μ1 和μ2，协方差矩阵分别为Σ1 和Σ2．给定一个样本x，要判断x 来自哪个总体．首先考虑两个总体X1 和X2 的协方差矩阵相同的情况，即μ1 ≠μ2,Σ1＝Σ2＝Σ．要判断x 来自哪个总体，需要计算x 到总体X1 和X2 的马氏距离的平方d2（x，X1）和d2（x，X2），然后进行

以下我们来讨论两个总体的距离判别，分别讨论两个总体协方差矩阵相同和不同的情况．

设总体X1 和X2 的均值向量分别为μ1 和μ2，协方差矩阵分别为Σ1 和Σ2．给定一个样本x，要判断x 来自哪个总体．

首先考虑两个总体X1 和X2 的协方差矩阵相同的情况，即

μ1 ≠μ2,Σ1＝Σ2＝Σ．

要判断x 来自哪个总体，需要计算x 到总体X1 和X2 的马氏距离的平方d2（x，X1）和d2（x，X2），然后进行比较．若d2（x，X1）≤d2（x，X2），则判定x属于X1；否则，则判定x 属于X2．由此得到如下判别准则：

以下引进判别函数的表达式，考虑d2（x，X1）和d2（x，X2）的关系，则有

其中， pagenumber_ebook=155,pagenumber_book=146 为两个总体均值的平均．

令

称ω（x）为两个总体的距离判别函数．

因此，判别准则（8．1．3）变为

在实际计算中，总体的均值μ1，μ2 和协方差矩阵Σ 均未知，因此需要用样本均值和样本协方差矩阵来代替．设是来自总体X1 样本，是来自总体X2 样本，则样本均值和样本协方差矩阵分别为

其中，(www.chuimin.cn)

对于待判样本x，其判别函数定义为

其中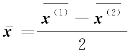， pagenumber_ebook=156,pagenumber_book=147 ．其判别准则为

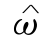注意到判别函数（8．1．9）是线性函数，因此，在两个总体的协方差矩阵相同的情况下，距离判别属于线性判别，称为判别系数．从几何角度上来看， pagenumber_ebook=156,pagenumber_book=147 （x）＝0表示一张超平面，将整个空间分成R1，R2 两个半空间．

再考虑两个总体X1 和X2 的协方差矩阵不同的情况，即

μ1 ≠μ2,Σ1 ≠Σ2．

对于样本x，在协方差矩阵不同的情况，判别函数为

与前面讨论的情况相同，在实际计算中，总体均值和协方差矩阵未知，同样需要用样本的均值和样本协方差矩阵来代替．因此，对于对于待判样本x，其判别函数定义为

其中，

其判别准则与式（8．1．10）的形式相同．

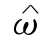由于和一般不会相同，所以函数（8．1．12）是二次函数．因此，在两个总体的协方差矩阵不相同的情况下，距离判别属于二次判别．从几何角度上来看， pagenumber_ebook=157,pagenumber_book=148 （x）＝0表示一张二次曲面．