首页理论教育城镇居民消费支出的聚类分析报告

城镇居民消费支出的聚类分析报告

2023-11-18 理论教育版权反馈

【摘要】：在实验7．4．2中31个样品进行了聚类分析．现在对实验7．4．2中的8个变量进行聚类分析．在实验7．4．2的基础上，先求相关矩阵＞cor结果如下：根据的相关矩阵画8个变量的聚类图＞names＜-c＞r＜-matrix＞d＜-as．dist(1－r);hc＜-hclust;dend＜-as．dendrogram＞nP＜-list＞add E＜-function{＋if(!

在实验7．4．2中31个样品（省市和自治区）进行了聚类分析．现在对实验7．4．2中的8个变量进行聚类分析．

（1）在实验7．4．2的基础上，先求相关矩阵

＞cor(X)

结果如下：

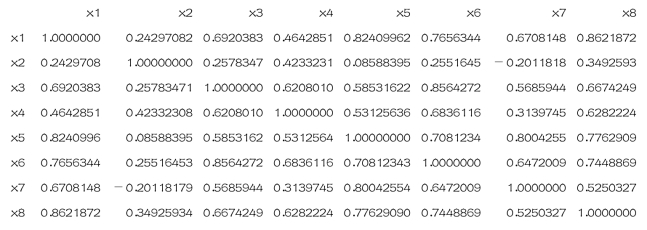
pagenumber_ebook=148,pagenumber_book=139

（2）根据（1）的相关矩阵画8个变量的聚类图

＞names＜-c(＂x1＂,＂x2＂,＂x3＂,＂x4＂,＂x5＂,＂x6＂,＂x7＂,＂x8＂)

＞r＜-matrix(cor(X),nrow＝8,dimnames＝list(names,names))

＞d＜-as．dist(1－r);hc＜-hclust(d);dend＜-as．dendrogram(hc)

＞nP＜-list(col＝3：2,cex＝c(2．0,0．75),pch＝21：22,

＋bg＝c(＂light blue＂,＂pink＂),

＋lab．cex＝1．0,lab．col＝＂tomato＂)

＞add E＜-function(n){

＋if(!is．leaf(n)){

＋attr(n,＂edgePar＂)＜-list(p．col＝＂plum＂)

＋attr(n,＂edgetext＂)＜-paste(attr(n,＂members＂),＂members＂)

＋}

＋n

＋}

＞de＜-dendrapply(dend,add E);plot(de,node Par＝n P)

结果如图7-3所示．

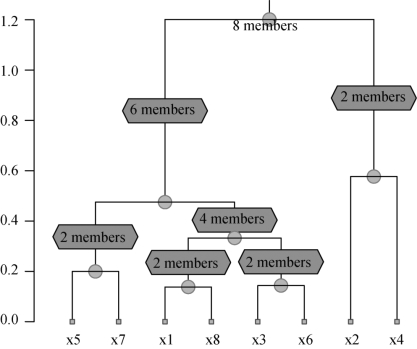
pagenumber_ebook=149,pagenumber_book=140

图7-3　8个变量的聚类图

从图7-3可以看出，x1，x8 先并为一类，其次是x3，x6 并为一类，再合并就是新得到的两类合并为一类，然后合并就是x5，x7 合并为一类，再往下合并就是x2，x4 最后合并为一类．

在聚类过程中类的个数如何确定才适宜呢？至今没有令人满意的方法．在R软件中，与确定类的个数有关的函数是“rect．hclust（）”，它本质上是由类的个数或阈值来确定聚类的情况，其调用格式为

rect．hclust(t ree,k＝NULL,which＝NULL,x＝NULL,h＝NULL,border＝2,cluster＝NULL)(www.chuimin.cn)

其中，“tree”是由hclust生成的结构；k 是类的个数；h 是聚类图中的阈值；border是数或向量，标明矩形框的颜色．

在前面的问题中，如果分为2类，即k＝2，其R 代码如下：

plclust(hc,hang＝－1);re＜－rect．hclust(hc,k＝2)

结果如图7-4所示．

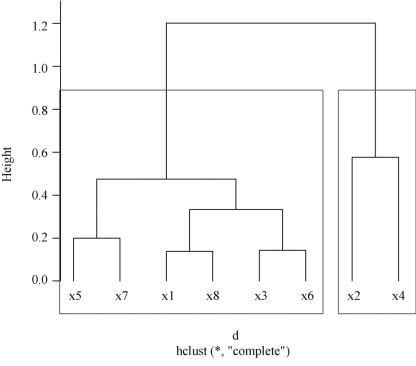
pagenumber_ebook=150,pagenumber_book=141

图7-4　8个变量的聚类图（k＝2）

从图7-4可以看出，x5，x7，x1，x8，x3，x6 为第一类；x2，x4 为第二类．

在前面的问题中，如果分为3类，即k＝3，其R 代码如下：plclust（hc，hang＝－1）；re＜-rect．hclust（hc，k＝3）

结果如图7-5所示．

以图7-5可以看出，x5，x7，x1，x8，x3，x6 为第一类；x2 为第二类；x4 为第三类．

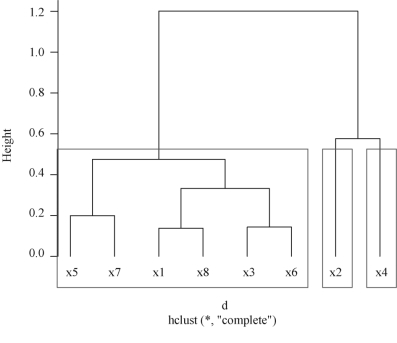
pagenumber_ebook=151,pagenumber_book=142

图7-5　8个变量的聚类图（k＝3）

在前面的问题中，如果分为4类，即k＝4，其R 代码如下：

plclust(hc,hang＝－1);re＜-rect．hclust(hc,k＝4)

结果如图7-6所示．

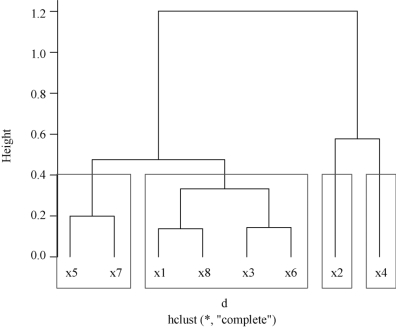
pagenumber_ebook=151,pagenumber_book=142

图7-6　8个变量的聚类图（k＝4）

从图7-6可以看出，x5，x7 为第一类；x1，x8，x3，x6 为第二类；x2 为第三类；x4 为第四类．

在前面的问题中，如果分为5类，即k＝5，其R 代码如下：

plclust(hc,hang＝－1);re＜-rect．hclust(hc,k＝5)

结果如图7-7所示．

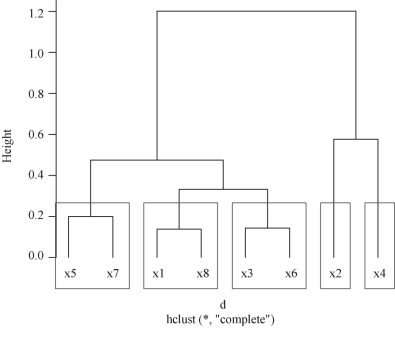
pagenumber_ebook=152,pagenumber_book=143

图7-7　8个变量的聚类图（k＝5）

从图7-7可以看出，x5，x7 为第一类；x1，x8 为第二类；x3，x6 为第三类；x2 为第四类；x4 为第五类．