多元线性回归的数学模型可以用矩阵形式表示为1.参数β的最小二乘估计设b0,b1,…表4-1 回归正交设计计算表通过推导,可以得到方差分析表4-2。表4-2 方差分析表3.回归方程的显著性检验F>Fα 若式成立,我们可以认为在显著水平α下,线性回归方程(4-6)是有显著意义的。反之,则认为线性回归方程没有什么意义,这时需要查明原因,具体情况具体分析。......
2023-06-27
设有n 个样品的多元观测数据xi=(xi1,xi2,…,xip)T,i=1,2,…,n.此时,每个样品可以看成p 维空间的一个点,n 个样品组成p 维空间的n 个点.我们自然用各点之间的距离来衡量各样品之间的相似性程度(或靠近程度).
设d(xi,xj)是样品xi 和xj 之间的距离,一般要求它满足下列条件:
(1)d(xi,xj)≥0,且d(xi,xj)=0当且仅当xi=xj;
(2)d(xi,xj)=d(xj,xi);
(3)d(xi,xj)≤d(xi,xk)+d(xk,xj).
在聚类分析中,有些距离不满足(3),我们在广义的意义下仍然称它为距离.
以下介绍聚类分析中常用的距离.常用的距离有欧氏(Euclidean)距离、绝对距离、马氏(Mahalanobis)距离等.
假定有n 个样品的多元数据,对于i,j=1,2,…,n,d(xi,xj)为p 维点(向量)xi=(xi1,xi2,…,xip)T 和xj=(xj1,xi2,…,xjp)T 之间的距离,记为dij=d(xi,xj).
(1)欧氏距离(www.chuimin.cn)
欧氏距离是最常用的,它的主要优点是当坐标轴进行旋转时,欧氏距离是保持不变的.因此,如果对原坐标系进行平移和旋转变换,则变换后样本点间的距离和变换前完全相同.
称
为距离矩阵,其中dij=dji(这说明距离矩阵是对称矩阵).
(2)绝对距离
(3)马氏距离
其中,S 是由x1,x2,…,xn 得到的协方差矩阵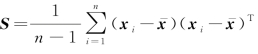 ,
, .
.
显然,当S 为单位矩阵时,马氏距离即化简为欧氏距离.在实际问题中协方差矩阵S 往往是未知的,常需要用样本协方差矩阵来估计.需要说明的是,马氏距离对一切线性变换都是不变的,所以不受量纲的影响.
值得注意的是,当变量的量纲不同时,观测值的变异范围相差悬殊时,一般首先对数据进行标准化处理,然后再计算距离.
有关应用多元统计分析:基于R的实验的文章

多元线性回归的数学模型可以用矩阵形式表示为1.参数β的最小二乘估计设b0,b1,…表4-1 回归正交设计计算表通过推导,可以得到方差分析表4-2。表4-2 方差分析表3.回归方程的显著性检验F>Fα 若式成立,我们可以认为在显著水平α下,线性回归方程(4-6)是有显著意义的。反之,则认为线性回归方程没有什么意义,这时需要查明原因,具体情况具体分析。......
2023-06-27

观察与思考在平面直角坐标系中,任何一点P都可以用有序实数对(x,y)表示,我们把(x,y)叫做点P的坐标,记作P(x,y).如果给出了两个点的坐标,应如何计算这两点间的距离并确定这两个点的中点位置呢?......
2023-11-22

根据上面的叙述,要选择样本空间Ω 的一个划分R1 和R2=Ω-R1,使得平均误判损失ECM 达到极小.定理8.3.1 极小化平均误判损失式的区域R1 和R2 为说明:当时,即x 为边界点,它可以归入R1 和R2中的任何一个,为了方便就将它归入R1.根据定理8.3.1,得到两总体的Bayes判别准则:应用此准则时仅需要计算:新样本点x0=(x01,x02,…......
2023-11-18

原来检验果汁中含铅量有三种方法A1,A2,A3,现研究出另一种快速检验法A4,能否用A4 代替前三种方法,需要通过实验考察.观察的对象是果汁,不同的果汁当做不同的水平:B1 为苹果,B2 为葡萄汁,B3 为西红柿汁,B4 为苹果饮料汁,B5 桔子汁,B6 菠萝柠檬汁.现进行双因素交错搭配试验,即用四种方法同时检验每一种果汁,其检验结果见表6-8.问因素A和B对果汁的含铅量是否有显著影响?......
2023-11-18

,xn 是从一元总体中抽取的.一元数据的数字特征主要有:均值,方差s2=,标准差s=,等等.对于多元数据,除分析各分量的取值特征外,还要分析各分量之间的相关关系.由于多元统计分析中的符号多而杂,因此需要说明:在一元统计学中一般用大写和小写字母分别来区分随机变量及其观测值,在本书后面的章节里,由于其他复杂的符号,我们可能不再遵守此约定,请读者注意一个符号在每一章中的意义.......
2023-11-18

因子分析是用少数几个公共因子去提取研究对象的绝大部分信息,既减少了因子的数目,又把握住了研究对象的相互关系.在因子分析中根据研究对象的不同,分为R 型和Q 型,如果研究变量的相互关系时则采用R 型因子分析;如果研究样品间相互关系时则采用Q 型因子分析.但无论是R 型或Q 型都未能很好地揭示变量和样品间的双重关系,另一方面当样品容量n 很大(如n>1 000),进行Q型因子分析时,计算n 阶方阵的特......
2023-11-18

对于广义线性模型,除了以上介绍的Logistic回归模型外,还有其他的模型,如Poisson模型,这里就不作详细介绍.以下简要介绍R 软件中“glm( )”关于这些模型的使用方法.Poisson分布族模型和拟Poisson分布族模型的使用方法如下:fm<-glmfm<-glm其直观意义是ln[E]=β0+β1x1+β2x2+…+βp xp,即E=exp(β0+β1 x1+β2 x2+…......
2023-11-18

以下我们来讨论两个总体的距离判别,分别讨论两个总体协方差矩阵相同和不同的情况.设总体X1 和X2 的均值向量分别为μ1 和μ2,协方差矩阵分别为Σ1 和Σ2.给定一个样本x,要判断x 来自哪个总体.首先考虑两个总体X1 和X2 的协方差矩阵相同的情况,即μ1 ≠μ2,Σ1=Σ2=Σ.要判断x 来自哪个总体,需要计算x 到总体X1 和X2 的马氏距离的平方d2(x,X1)和d2(x,X2),然后进行......
2023-11-18
相关推荐