在实验2．3．1中，我们对mtcars数据集（R 自带数据集）进行了展示和描述，以下对该数据集进行可视化．（1）汽车每加仑英里数直方图＞hist(mtcars＄mpg,breaks＝10)结果如图2-1所示．（2）按汽缸数划分的各车型车重的核密度图＞par(lwd＝2)＞library(sm)＞cyl．f＜－factor(mtcars＄cyl,levels＝c(4,6,8),labels＝c(＂4......
2023-11-18
UScereal数据集方差分析：基于R的多元统计分析应用
【摘要】：用MASS包中的UScereal数据集，我们研究美国谷物中的卡路里、脂肪和糖含量是否会因为储存架位置的不同而发生变化．其中1代表底层货架，2代表中层货架，3代表顶层货架．卡路里（calories）、脂肪（fat）和糖（sugars）含量是因变量，货架是3水平（1，2，3）的自变量．（1）单因素多元方差分析在以上代码中，“cbind（ ）”函数将三个变量（calories，fat，sugars）合并
用MASS包中的UScereal数据集，我们研究美国谷物中的卡路里、脂肪和糖含量是否会因为储存架位置的不同而发生变化．其中1代表底层货架，2代表中层货架，3代表顶层货架．卡路里（calories）、脂肪（fat）和糖（sugars）含量是因变量，货架是3水平（1，2，3）的自变量．
（1）单因素多元方差分析
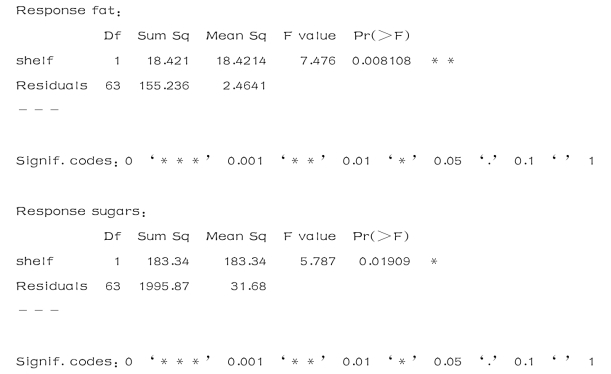
在以上代码中，“cbind（ ）”函数将三个变量（calories，fat，sugars）合并成一个矩阵．“aggregate（ ）”函数可获取货架的各个均值，“cov（ ）”函数则输出个谷物间的方差和协方差．“manova（ ）”函数能对组间差异进行多元检验．上面的结果F 值显著，说明三个组的营养成分的观测值不同．由于多元检验是显著地，因此可以用“summary．aov（ ）”函数对每一个变量作单因素方差分析．从上述结果可以看出，三组的营养成分的观测值都是不同的．
（2）评估假设检验
单因素多元方差分析有两个前提假设，一个是多元正态性，另一个是方向-协方差矩阵同质性．第一个假设是指因变量组成合成的向量服从一个多元正态分布，可用QQ 图来验证该假设条件．
如果有p×1的多元正态随机向量x，均值为u，协方差矩阵为W，那么x 与u 的马氏距离的平方服从自由度为p 的卡方分布．Q-Q 图展示卡方分布的分位数，横、纵坐标分别表示样本量和马氏距离的平方值．如果全部点落在斜率为1、截距为0的直线上，则表明数据服从多元正态分布．
检验多元正态性，其代码如下：
＞center＜－colMeans(y)
＞n＜－nrow(y)
＞p＜－ncol(y)
＞cov＜－cov(y)
＞d＜－mahalanobis(y,center,cov)
＞coord＜－qqplot(qchisq(ppoints(n),d f＝p),
＋d,main＝＂Q－Q plot Assessing Multivariate Normality＂,
＋ylab＝＂mahalanobis D2＂)
＞abline(a＝0,b＝1)
＞identify(coord＄x,coord＄y,labels＝row．names(UScereal))(www.chuimin.cn)
结果如图6-7所示．
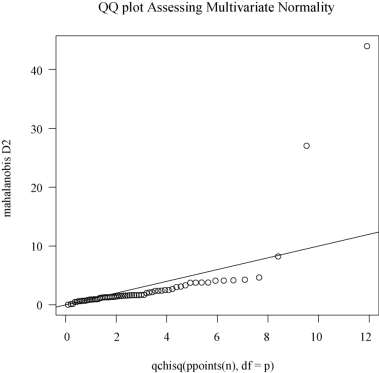
图6-7 检验多元正态性的QQ 图
使用mvoutlier包中的“aq．plot（ ）”函数来检验多元离群点，其代码如下：
＞library(mvoutlier)
＞outliers＜－aq．plot(y)
＞outliers
结果如图6-8所示．
从图6-8可以看到，数据中有离群点．
（3）稳健多元方差分析
如果多元正态性或者方差-协方差均值假设都不满足，又或者担心多元离群点，那么可以考虑用稳健检验．稳健单因素MANOVA 可通过rrcov包中的“Wilks．test（ ）”函数实现．代码如下：
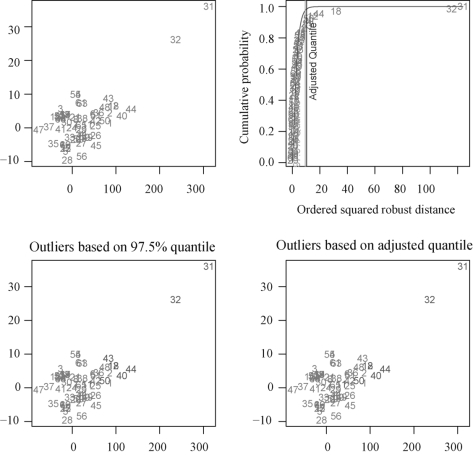
图6-8 检验多元离群点图
＞library(rrcov)
＞Wilks．test(y,shelf,method＝＂mcd＂)
结果如下：
从以上结果来看，稳健检验对离群点和违反MANOVA 假设的情况不敏感，而且再一次验证了储存在货架顶部、中部和底部的谷物营养成分含量不同．
有关应用多元统计分析：基于R的实验的文章
- 详细阅读
-
基于R的应用多元统计分析成果详细阅读
，F5 的线性组合表示出来Xi＝μi＋ai1 F1＋ai2 F2＋…，F5 的值却是未知的，有关参数的意义也有很大的差异．因子分析的首要任务就是估计因子载荷aij 和方差σ2i，然后给因子Fi 一个合理的解释，若难以进行合理的解释，则需要进一步作因子旋转，希望旋转后能发现比较合理的解释．特别需要说明的是这里的因子和试验设计里的因子（或因素）是不同的，它比较抽象和概括，往往是不可以单独测量的．......
2023-11-18
-
多元统计分析：R实验中的mtcars数据集回详细阅读
在实验2．3．1中，我们对mtcars数据集进行了展示和描述．在实验2．3．3中，我们对mtcars数据集进行了可视化．现在我们对该数据集中的变量进行回归分析．（1）不考虑变量交互项对该数据集，如果把mpg（汽车每加仑公里数）作为因变量，自变量为hp（马力）和wt（汽车重量）进行回归．＞fit＜－lm(mpg～hp＋wt,data＝mtcars)＞summary(fit)结果如下：得到的回归方程为......
2023-11-18
-
应用多元统计分析方法：基于R实验详细阅读
多元统计分析是统计学中应用性很强的一个分支，它的应用范围十分广泛．多元统计分析可以应用于几乎所有的领域，主要包括经济学、农业、地质学、医学、工业、气象学、金融、精算、物理学、地理学、军事科学、文学、法律、环境科学、考古学、体育科学、遗传学、教育学、生物学、管理科学、水文学等，还有一些交叉学科或方向等．多元统计分析的应用实在是难以一一罗列，以下简要地介绍一下多元统计分析在文学、数据挖掘（作为交叉学科......
2023-11-18
-
基于R的多元统计分析：Bayes判别详细阅读
根据上面的叙述，要选择样本空间Ω 的一个划分R1 和R2＝Ω－R1，使得平均误判损失ECM 达到极小．定理8．3．1 极小化平均误判损失式的区域R1 和R2 为说明：当时，即x 为边界点，它可以归入R1 和R2中的任何一个，为了方便就将它归入R1．根据定理8．3．1，得到两总体的Bayes判别准则：应用此准则时仅需要计算：新样本点x0＝（x01，x02，…......
2023-11-18
-
应用多元统计分析：基于R的典型相关数学描述详细阅读
，Y为来自总体容量为n 的样本，这时协方差矩阵的无偏估计为其中，用代替Σ 并按式和式求出 和，，称 为样本的典型相关系数，称（i＝1，2，…，q）为样本的典型变量．计算时也可从样本的相关系数矩阵出发求样本的典型相关系数和典型变量，将相关系数矩阵取代协方差阵，计算过程是一样的．如果复相关系数中的一个变量是一维的，那么也可以称为偏相关系数．偏相关系数是描述一个随机变量y 与多个随机变量X＝（x1，x2，…......
2023-11-18
-
应用多元统计分析：基于R的实验方法简介详细阅读
如果是，建立变量之间的定量关系式，并用于预测或控制——回归分析．变量之间的相互关系：分析两组变量之间的相互关系——典型相关分析．多元数据的统计推断这是关于参数估计和假设检验的问题．特别是多元正态分布的均值向量和协方差矩阵的估计和假设检验等问题．多元统计分析的理论基础多元统计分析的理论基础包括多维随机向量，以及由此定义的各种多元统计量，推导它们的分布并研究其性质，研究它们的抽样分布理论．......
2023-11-18
-
广义线性模型概述：应用多元统计分析基于R实验详细阅读
，βp的线性函数．因此，对μ 作变换，则可得到下面几种分布的连接函数的形式：正态分布m（μ）＝μ＝∑βi xi．二项分布．Poisson分布m（μ）＝lnμ＝∑βi xi．上述推广体现在以下两个方面：通过一个连接函数，将响应变量的期望与解释变量建立线性关系m[E]＝β0＋β1 x1＋β2 x2＋…......
2023-11-18
相关推荐