多元统计分析是统计学中应用性很强的一个分支，它的应用范围十分广泛．多元统计分析可以应用于几乎所有的领域，主要包括经济学、农业、地质学、医学、工业、气象学、金融、精算、物理学、地理学、军事科学、文学、法律、环境科学、考古学、体育科学、遗传学、教育学、生物学、管理科学、水文学等，还有一些交叉学科或方向等．多元统计分析的应用实在是难以一一罗列，以下简要地介绍一下多元统计分析在文学、数据挖掘（作为交叉学科......
2025-09-30
多元统计分析揭示果汁含铅差异
【摘要】：原来检验果汁中含铅量有三种方法A1，A2，A3，现研究出另一种快速检验法A4，能否用A4 代替前三种方法，需要通过实验考察．观察的对象是果汁，不同的果汁当做不同的水平：B1 为苹果，B2 为葡萄汁，B3 为西红柿汁，B4 为苹果饮料汁，B5 桔子汁，B6 菠萝柠檬汁．现进行双因素交错搭配试验，即用四种方法同时检验每一种果汁，其检验结果见表6-8．问因素A和B对果汁的含铅量是否有显著影响？
原来检验果汁中含铅量有三种方法A1，A2，A3，现研究出另一种快速检验法A4，能否用A4 代替前三种方法，需要通过实验考察．观察的对象是果汁，不同的果汁当做不同的水平：B1 为苹果，B2 为葡萄汁，B3 为西红柿汁，B4 为苹果饮料汁，B5 桔子汁，B6 菠萝柠檬汁．现进行双因素交错搭配试验，即用四种方法同时检验每一种果汁，其检验结果见表6-8．问因素A（检验方法）和B（果汁品种）对果汁的含铅量是否有显著影响？
表6-8 果汁含铅比实验数据
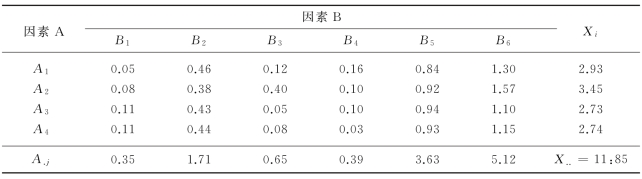
（1）首先根据表6-8建立数据框
juice＜－data．frame(
X＝c(0．05,0．46,0．12,0．16,0．84,1．30,0．08,0．38,0．4,
0．10,0．92,1．57,0．11,0．43,0．05,0．10,0．94,1．10,
0．11,0．44,0．08,0．03,0．93,1．15),
A＝gl(4,6),
B＝gl(6,1,24)
)
注：这里函数“gl（ ）”用来给出因子水平，其调用格式为
gl(n,k,length＝n∗k,labels＝1：n,ordered＝FALSA)
说明：n 是水平数，k 是每一水平上的重复次数，length 是总观测值数，ordered指明各水平是否先排序．(https://www.chuimin.cn)
（2）作双因素方差分析
＞juice．aov＜－aov(X～A＋B,data＝juice)
＞summary(juice．aov)
结果如下：
以上p 值说明果汁品种（因素B）对含铅量有显著影响，而没有充分理由说明检验方法（因素A）对含铅量有显著影响．
（3）用函数“bartlett．test（ ）”分别对因素A 和因素B作方差的齐性检验
＞bartlett．test(X～A,data＝juice)
结果如下：
结果如下：
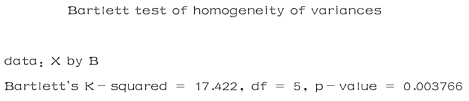
以上结果说明：对因素A，p 值（0．966）远大于0．05，接受原假设，认为因素A的各水平下的数据是等方差的；对因素B，p 值（0．003766）小于0．05，拒绝原假设，即认为因素B不满足方差齐性要求．
相关文章
- 详细阅读
-
基于性格特征，揭示用户感知差异详细阅读
从表中结果可以看到，对于不同性格特征的用户而言，所有潜在变量的样本均值比较均存在显著性差异，表明不同性格特征的用户对信息需求、学术信息搜寻行为、信息有用性、信息质量、服务质量、系统质量以及信息源可信度的感知存在显著差异，因此，零假设H21被拒绝。......
2025-09-29
-
如何在应用多元统计分析中选择变量？详细阅读
，Xp 之间并不是完全独立的，而是有一定的相关性存在的．如果回归模型中有某两个自变量Xi 和Xj 的相关系数比较大，就可使正规方程组的系数矩阵出现病态，也就是所谓的多重共线性的问题，将导致回归系数的估计值的精度不高．因此，适当地选择变量以建立一个“最优”的回归方程是十分重要的．那么什么是“最优”回归方程呢？......
2025-09-30
-
多元统计分析：用R进行回归分析详细阅读
women数据集（R 自带数据集）提供了15个年龄在30～39岁之间女性的身高和体重的信息．（1）查看women数据集（身高和体重）的信息＞women结果如下：（2）weight和height的简单线性回归＞fit＜－lm(weight～height,data＝women)＞summary(fit)结果如下：由此得到的回归方程为从以上结果可以看出，回归方程通过检验．（3）身高和体重的散点图以及回归......
2025-09-30
-
多元统计分析：对数线性模型的应用详细阅读
对于广义线性模型，除了以上介绍的Logistic回归模型外，还有其他的模型，如Poisson模型，这里就不作详细介绍．以下简要介绍R 软件中“glm（ ）”关于这些模型的使用方法．Poisson分布族模型和拟Poisson分布族模型的使用方法如下：fm＜－glmfm＜－glm其直观意义是ln[E]＝β0＋β1x1＋β2x2＋…＋βp xp,即E＝exp(β0＋β1 x1＋β2 x2＋…......
2025-09-30
-
中国居民媒介使用调查：城际差异揭示详细阅读
本次调查根据第一财经新一线城市研究所发布的《2019城市商业魅力排行榜》，将调查者所在的城市分为一线城市、新一线城市、二线城市、三线城市、四线城市和五线城市。[1]在本次调查样本中，一线城市样本占13.2%，新一线城市样本占37%，二线城市样本占26.7%，三线城市样本占12.4%，四线城市样本占8.8%，五线城市样本占2.0%。图2-1不同城市级别的物理媒介使用频率......
2025-09-30
-
广义线性模型概述：应用多元统计分析基于R实验详细阅读
，βp的线性函数．因此，对μ 作变换，则可得到下面几种分布的连接函数的形式：正态分布m（μ）＝μ＝∑βi xi．二项分布．Poisson分布m（μ）＝lnμ＝∑βi xi．上述推广体现在以下两个方面：通过一个连接函数，将响应变量的期望与解释变量建立线性关系m[E]＝β0＋β1 x1＋β2 x2＋…......
2025-09-30
-
多元统计分析：线性回归方程的确定和影响检验详细阅读
，Xp 来表示．在回归分析中，主要研究以下问题：确定Y 与X1，X2，…，Xp 之间的定量关系表达式，这种表达式称为回归方程；对所得到的回归方程的可信程度进行检验；判断自变量Xi（i＝1，2，…，p）对因变量Y 有无显著影响；利用所求得的回归方程进行预测或控制．......
2025-09-30
相关推荐