，Ar，因素B 有s个水平B1，B2，…，Bs．每一个水平组合下重复试验t次．记录第k 次的观测值为xijk，把观测数据列表，见表6-6．表6-6双因素重复试验数据假定xijk～N（i＝1，2，…，t）且各xijk 相互独立，因此模型可以归结为其中，αi 为因素A 第i个水平的效应，βj 为因素B 第j个水平的效应，δij 为Ai 和Bj的交互效应．因此有．此时，判断因素A，B 交互效应的影响是否显著等价于下列检验假设：H01：α1＝α2＝…......
2023-11-18
不考虑交互作用的多元统计分析结果
【摘要】：，s）且各xij 相互独立．不考虑两因素的交互作用，因此模型可以归结为其中，为总平均；αi 为因素A 第i个水平的效应；βj 为因素B 第j 个水平的效应．在线性模型下，方差分析的主要任务是系统分析因素A 和因素B 对试验指标影响的大小．因此，在给定显著性水平α 下，提出以下统计假设：对于因素A，“因素A 对试验指标影响不显著”等价于H01：α1＝α2＝…
因素A，B 的每一个水平组合（Ai，Bj）下进行一次独立试验得到观测值xij（i＝1，2，…，r；j＝1，2，…，s）．观测数据见表6-4．
表6-4 无重复试验的双因素方差分析数据
假定xij～N（μij，σ2）（i＝1，2，…，r；j＝1，2，…，s）且各xij 相互独立．不考虑两因素的交互作用，因此模型可以归结为
其中，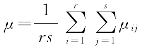
为总平均；αi 为因素A 第i个水平的效应；βj 为因素B 第j 个水平的效应．
在线性模型（6．2．1）下，方差分析的主要任务是系统分析因素A 和因素B 对试验指标影响的大小．因此，在给定显著性水平α 下，提出以下统计假设：对于因素A，“因素A 对试验指标影响不显著”等价于
H01：α1＝α2＝…＝αr＝0．
对于因素B，“因素B 对试验指标影响不显著”等价于
H02：β1＝β2＝…＝βs＝0．
双因素方差分析与单因素方差分析的统计原理基本相同，也是基于平方和分解公式
ST＝SE＋SA＋SB,
其中，
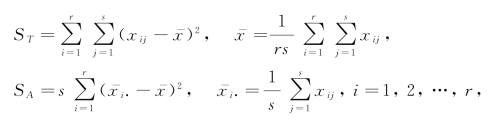(www.chuimin.cn)
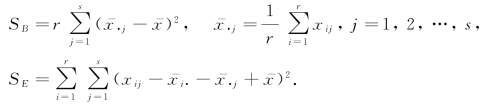
ST 为总离差平方和，SE 为误差平方和，SA 为由因素A 的不同水平所引起的离差平方和（称为因素A 的平方和）．类似地，SB 称为因素B 的平方和．可以证明，当H01 成立时，
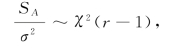
且与SE 相互独立，而
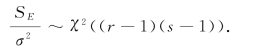
于是当H01 成立时，
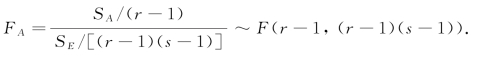
类似地，当H02 成立时，
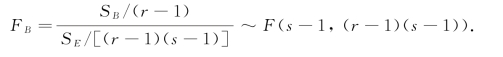
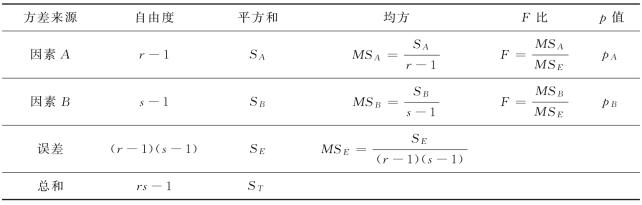
分别以FA 和FB 作为H01 和H02 的检验统计量，把计算结果列成方差分析表，见表6-5．
表6-5 双因素方差分析表
有关应用多元统计分析：基于R的实验的文章
- 详细阅读
-
实验结果：老鼠存活时间多元统计分析详细阅读
有一个关于检验毒药强弱的实验，给48只老鼠注射I，II，III三种毒药（因素A），同时有A，B，C和D 四种治疗方案（因素B），这样的试验在每一种因素组合下都重复四次测试老鼠的存活时间，数据见表6-9．试分析毒药和治疗方案以及它们的交互作用对老鼠存活时间有无显著影响．表6-9老鼠存活时间（年）的实验数据（1）根据表6-9以数据框形式导入数据，并用函数“plot（ ）”作图＞rats＜－data．......
2023-11-18
-
典相关系数检验结果-应用多元统计分析详细阅读
，s）至少有一个非零．记经计算得在原假设为真的情况下，检验的统计量近似服从自由度为pq 的χ2 分布．在给定的显著水平α 下，如果，则拒绝原假设，认为至少第一对典型变量之间的相关性显著．部分总体典型相关系数为零的检验H0：λ2＝λ3＝…＝λs＝0，H1：λi（i＝3，4，…＝λs＝0，H1：λi（i＝k，k＋1，…......
2023-11-18
-
交互作用在实证结果中的分析详细阅读
社区层次的斜率系数模型中，各变量未能通过显著性检验。但未能通过显著性检验，可能是由于农户信任差异性相互抵消，导致不显著。社区变量中村庄地形通过了显著性检验，表明社区因素中社会参与会因村庄地形的平坦强化合作意愿，与预期假设不一致这可能的原因是平坦地区地理位置临近，为农户集体治理和民主自治提供便利条件，长期的诉求表达会驱使农户合作。表8-3交互作用的估计结果......
2023-06-28
-
基于R的多元统计分析：Bayes判别详细阅读
根据上面的叙述，要选择样本空间Ω 的一个划分R1 和R2＝Ω－R1，使得平均误判损失ECM 达到极小．定理8．3．1 极小化平均误判损失式的区域R1 和R2 为说明：当时，即x 为边界点，它可以归入R1 和R2中的任何一个，为了方便就将它归入R1．根据定理8．3．1，得到两总体的Bayes判别准则：应用此准则时仅需要计算：新样本点x0＝（x01，x02，…......
2023-11-18
-
基础多元线性回归统计分析详细阅读
多元线性回归的数学模型可以用矩阵形式表示为1.参数β的最小二乘估计设b0，b1，…表4-1 回归正交设计计算表通过推导，可以得到方差分析表4-2。表4-2 方差分析表3.回归方程的显著性检验F＞Fα 若式成立，我们可以认为在显著水平α下，线性回归方程（4-6）是有显著意义的。反之，则认为线性回归方程没有什么意义，这时需要查明原因，具体情况具体分析。......
2023-06-27
-
桥梁可靠度分析：考虑车重增长的结果详细阅读
考虑车重的线性增长系数为a，则到运营期的第n年为止，累积疲劳损伤函数可表示为：由此得出100年内顶板-U肋的细节疲劳损伤如图9.5所示。表9.3考虑车重增长的100年后顶板-U肋细节疲劳可靠指标由表9.3可知，当车重的线性增长系数为0.6%时，行车道顶板-U肋细节疲劳可靠指标为1.57，超车道位置处为2.49。......
2023-09-19
-
两点距离：多元统计分析要领详细阅读
，xjp）T 之间的距离，记为dij＝d．欧氏距离欧氏距离是最常用的，它的主要优点是当坐标轴进行旋转时，欧氏距离是保持不变的．因此，如果对原坐标系进行平移和旋转变换，则变换后样本点间的距离和变换前完全相同．称为距离矩阵，其中dij＝dji．绝对距离马氏距离其中，S 是由x1，x2，…......
2023-11-18
相关推荐