方差分析法及其检验统计量导出

2023-11-18 理论教育版权反馈

【摘要】：式等价于如果H0 被拒绝，则说明因素A 各水平的效应之间有显著的差异；否则，差异不明显．以下导出H0 的检验统计量．方差分析法是建立在平方和分解和自由度分解的基础上的，考虑统计量称ST 为总离差平方和，它是所有数据xij 与总平均值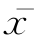的差的平方和，它描绘了所有数据的离散程度．可以证明如下平方和分解公式：其中，SE 表示随机误差的影响．这是因为对于固定的i 来讲，观测值xi1，xi2，…

式（6．1．2）等价于

如果H0 被拒绝，则说明因素A 各水平的效应之间有显著的差异；否则，差异不明显．

以下导出H0 的检验统计量．方差分析法是建立在平方和分解和自由度分解的基础上的，考虑统计量

pagenumber_ebook=114,pagenumber_book=105

称ST 为总离差平方和（或称总变差），它是所有数据xij 与总平均值 pagenumber_ebook=114,pagenumber_book=105 的差的平方和，它描绘了所有数据的离散程度．可以证明如下平方和分解公式：

其中，

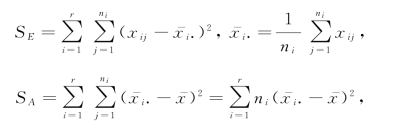
pagenumber_ebook=115,pagenumber_book=106

SE 表示随机误差的影响．这是因为对于固定的i 来讲，观测值xi1，xi2，…，xini 是来自同一个正态总体N（μi，σ2）的．因此，它们之间的差异是由随机误差所导致的．而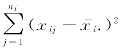 pagenumber_ebook=115,pagenumber_book=106 是这ni 个数据的变动平方和，正是它们的差异大小的度量．将r组这样的变动平方和相加，就得到了SE，通常称SE 为误差平方和或组内平方和．(www.chuimin.cn)

SA 表示在水平Ai 下样本均值与总均值之间的差异之和，它反映了r 个总体均值之间的差异．因为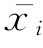 pagenumber_ebook=115,pagenumber_book=106 ·是第i个总体的样本均值，它是μi 的估计，因此r个总体均值μ1，μ2，…，μr 之间的差异越大，这些样本均值之间的差异越大．平方和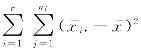正是这种差异大小的度量，这里ni 反映了第i个总体的样本大小在平方和SA 中的作用．称SA 为因素A 的效应平方和或组间平方和．

式（6．1．5）表明，总平方和ST 可按其来源分解成两个部分，一部分是误差平方和SE，它是由随机误差引起的；另一部分是因素A 的效应平方和SA，它是由因素A 各水平的差异引起的．

由模型假设（6．1．1），经过统计分析得到E（SE）＝（n－r）σ2，即 pagenumber_ebook=115,pagenumber_book=106 是σ2 的一个无偏估计，且．

如果假设H0 成立，则有E（SA）＝（r－1）σ2，即也是σ2 的一个无偏估计，且 pagenumber_ebook=115,pagenumber_book=106 ，并且SE 和SA 独立．因此，当假设H0 成立时，有

pagenumber_ebook=115,pagenumber_book=106

于是F 可以作为H0 的检验统计量．对于给定的显著性水平α，用Fα（r－1，n－r）表示F 分布的上α分位点．若F＞Fα（r－1，n－r），则拒绝原假设，认为因素A 的r个水平有显著差异．可以通过计算p 值的方法来决定是接受还是拒绝H0．其中p值为P{F（r－1，n－r）＞F}，它表示的是服从自由度为（r－1，n－r）的F分布的随机变量取值大于F 的概率．显然，p 值小于α 等价于F＞Fα（r－1，nr），表示在显著性水平α 下的小概率事件发生了，这意味着应该拒绝原假设H0．当p 值大于α，则不能拒绝原假设，所以应接受原假设H0．

通常将计算结果列成表6-2的形式，称为方差分析表．

表6-2　单因素方差分析表

pagenumber_ebook=116,pagenumber_book=107

方差分析法及其检验统计量导出

相关推荐