之后计算求得该组5个制品减重百分数的平均值xi，作为该组实验的结果。表6-9 实验结果表6-10 实验结果表6-11 实验结果表6-9～表6-11中，每一行为一组实验数据，各因素下为对应的水平号。表6-10～表6-11中实验号5、13、14的实验结果明显小于其他数据，后续数据处理中保留了这些数据，没有作为奇异项处理。图6-32 一个注塑周期的实验数据图所有数据统一在一个时间轴下记录，为后续数据分析提供了便利。......
2023-07-02
柑橘重量与直径的非线性模型-实验结果
【摘要】：在柑橘花定果后，每隔10天测量柑橘单果直径x 与单果重量y，有关数据见表5-3，试选择x 与y 之间最优模型．表5-3单果直径x 与单果重量y 的数据（1）输入表5-3的数据，并画出x 和y 的散点图＞x＝c(2．71,3．26,3．59,4．02,4．42,4．69,4．89,4．97,5．32,5．61,5．55,5．31)＞y＝c(11．49,18．68,24．07,40．10,55．70
在柑橘花定果后，每隔10天测量柑橘单果直径x 与单果重量y，有关数据见表5-3，试选择x 与y 之间最优模型．
表5-3 单果直径x 与单果重量y 的数据
（1）输入表5-3的数据，并画出x 和y 的散点图
＞x＝c(2．71,3．26,3．59,4．02,4．42,4．69,4．89,4．97,5．32,5．61,5．55,5．31)
＞y＝c(11．49,18．68,24．07,40．10,55．70,66．92,80．55,90．96,113．40,145．90,145．90,129．40)
＞plot(x,y)
结果如图5-3所示．
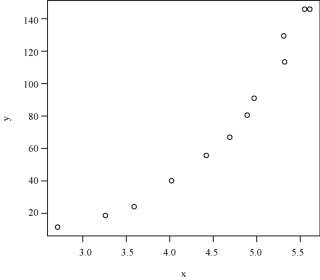
图5-3 散点图
从图5-3可以看出，表5-3中的x 和y 线性关系并不好，可拟合多项式、指数、对数、幂函数等曲线方程，以下分别拟合这些曲线来显示可线性化为直线的非线性回归方程．
（2）线性回归
结果如下：
求决定系数：
＞summary(lm．1)＄r．sq
结果如下：
[1]0．9077742
散点图加回归直线：
＞plot(x,y);abline(lm．1)
结果如图5-4所示．
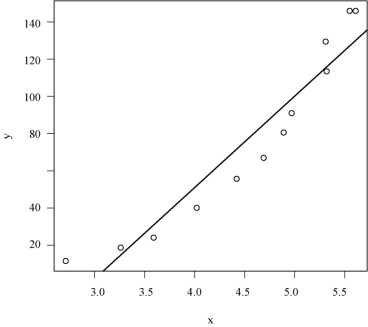
图5-4 散点图加回归直线
该模型的拟合优度（决定系数）为R2＝0．9077742，说明拟合效果并不好．
（3）多项式回归
用二次多项式y＝a＋bx＋cx2 来表示．作变量替换x1＝x，x2＝x2，将其转化为线性回归方程y＝a＋bx1＋cx2．(www.chuimin.cn)
多项式回归的结果如图5-5所示．
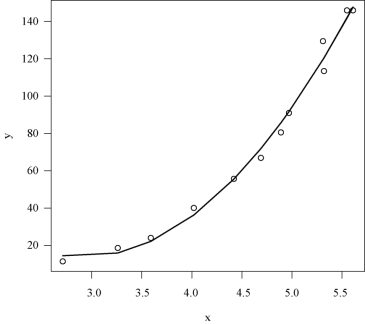
图5-5 多项式回归的结果
于是二次多项式为y＝169．88980－107．20144x＋18．40174x2，模型的拟合优度R2＝0．9903416，说明拟合效果比线性模型要好．
（4）指数法
指数曲线类型用方程y＝aebx 表示，用log y＝log a＋x 生成趋势曲线，其中，y′＝log y，a′＝log a，则可线性化为y′＝a′＋bx．
指数法的结果如图5-6所示．
根据以上计算结果，回归直线方程为
＝0．02221652＋0．89542001x，相应的指数曲线回归方程为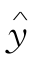
＝1．022465e0．89542001x．
图5-6 指数法的结果
该模型的拟合优度R2＝0．9967087，说明拟合效果好．
（5）幂函数法
幂函数的形式为y＝axb（a＞0）．对幂函数y＝axb 的两边求自然对数得log y＝log a＋b log x，用（log x，log y）生成趋势曲线，其中y′＝log y，x′＝log x，a′＝log a，则幂函数可线性化为y′＝a′＋bx′．
幂函数法的结果如图5-7所示．
根据以上计算结果，回归直线方程为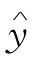
′＝－1．359583＋3．654890x′，相应的指数曲线回归方程为
＝0．2567678x3．654890．
该模型的拟合优度R2＝0．9899844，说明拟合效果比较好．
图5-7 幂函数法的结果
把以上几种拟合结果列表，见表5-4．
表5-4 模型的选择
从表5-4可以看出，指数法的拟合效果最好．
有关应用多元统计分析：基于R的实验的文章
- 详细阅读
-
水文模型的运行与结果分析详细阅读
本研究模拟了1971年到2000年这30年的水文过程，将模拟得到的逐日径流量与实测值进行比较，比较结果如表2所示。然而，模型模拟的低流量水文变量值低于实测值。随后进行了未来气候情景下的水文模型，在对结果的分析中考虑了前面提到的模型的不足。同样地，在模型应用之前，先用空间和时间尺度上插值生成的降水量数据对模型进行了率定和验证。......
2023-06-24
-
对比分析计算与实验结果详细阅读
峰值应力和破坏应变的相对误差小于5.13%。图8－18动能与内能之比表8－2不同单元尺寸下的峰值应力和失效应变Wu 等［8］和Rangaswamy 等［17］测量得到的PBX 9501 拉伸和压缩应力－应变曲线用于校准不同应变速率下的模拟结果。破坏应变分别为0.011 7、0.011 8 和0.012，与实验测得的0.011 7、0.011 9 和0.012 2 的破坏应变比较接近。图8－19测量和计算的应力－应变曲线拉伸；压缩应变率为10－4s－1；压缩应变率10－3s－1；压缩应变率10－2s－1......
2023-06-27
-
非线性数学模型线性化方法详细阅读
在建立控制系统的数学模型时，常常会遇到非线性的问题。严格地说，实际物理元件或系统都是非线性的。这种线性化方法称为小偏差线性化方法。通过上述讨论，在非线性数学模型进行线性化时应注意以下几点。若非线性特性是不连续的，处处不能满足展开成为泰勒级数的条件，这时就不能进行线性化处理。这类非线性称为本质非线性，对于这类问题，要用非线性自动控制理论来解决。......
2023-06-28
-
实验模型及方法详解详细阅读
实验采用对称的双断口结构，图6-25所示为实验模型的平面图及相关几何尺寸，单位均为mm。图6-25 气动斥力实验模型的平面图图6-26 气动斥力测试方法的原理图测量方法的原理如图6-26所示。下面的实验均是采用该方法进行的。图6-29 s=2mm，Im=4.2kA时的实验波形及电动斥力、气动斥力随时间的......
2023-06-15
-
肉桂酸的制备实验结果详细阅读
实验十六肉桂酸的制备（一）实验目的1.了解由Perkin反应制备肉桂酸的原理和方法。催化剂通常是相应酸酐的羧酸钾盐或钠盐，有时也可以用碳酸钾或叔胺代替，典型的例子就是肉桂酸的制备。注意：①安全管几乎插入底部以调节内压；②T型管的作用，③烧瓶D中的液体不宜超过其容积的1/3。本实验采用方法②重结晶，为防止溶剂挥发，使用回流冷凝装置。......
2024-08-20
-
切削温度结果分析：车削实验结果分析详细阅读
切削温度计算值与测试值之差相对误差也在5%的允许范围内，见图4-21b。图4-22 车削时切削温度与切削深度、进给量的特征曲面以及切削温度特征曲面等值线图a）切削温度与切削深度、进给量的特征曲面 b）切削温度特征曲面等值线图2.铣削实验结果分析由图4-23a可知，切削温度模型拟合得也较好。......
2023-06-27
-
性格特质模型的研究结果详细阅读
目前，五大性格特质模型是测量人们性格特质最常用的模型。五大类性格特质模型已被普遍应用于社会化媒体和信息行为等各种情境的研究中，如，Jadin等[210]研究虚拟的开放内容社区中性格特征对知识共享的影响。Heinstrm[215]的研究发现信息行为与性格特征的五个维度都有联系。Heinstrm[216]从心理学角度研究信息行为，将信息搜寻与性格特征、学习方式相联系，根据性格特征的不同组合确定了3种独特的信息搜寻模式。......
2023-08-03
相关推荐