挑战者号航天飞机O形环失效的统计分析成果

2023-11-18 理论教育版权反馈

【摘要】：1986年1月28日是寒冷的一天，在美国佛罗里达州的卡娜维拉尔角，“挑战者号”航天飞机升空后，因其O 形环密封圈失效，使高速飞行中的航天飞机在空气阻力的作用下于发射后的第73秒解体，机上7名宇航员全部罹难．“挑战者号”航天飞机正式发射任务前24次飞行发射时周围温度（单位：华氏度）和对应记录的损坏的O 形环数量见表5-2，其中x 为温度，y 为记录的损坏的O 形环数量．表5-2“挑战者号”航天飞机

1986年1月28日是寒冷的一天，在美国佛罗里达州的卡娜维拉尔角，“挑战者号”航天飞机升空后，因其O 形环密封圈失效，使高速飞行中的航天飞机在空气阻力的作用下于发射后的第73秒解体，机上7名宇航员全部罹难．

“挑战者号”航天飞机正式发射任务前24次飞行发射时周围温度（单位：华氏度）和对应记录的损坏的O 形环数量见表5-2，其中x 为温度，y 为记录的损坏的O 形环数量．

表5-2　“挑战者号”航天飞机发射温度和O 形环损坏数据

pagenumber_ebook=100,pagenumber_book=91

注：华氏（℉）温度与摄氏（℃）温度的关系：摄氏温度＝（华氏温度－32）/1．8．

请根据表5-2提供的数据建立模型；在温度为53（℉）时，预测O 形环损坏的概率；要使O 形环损坏的概率小于0．05，需要温度满足什么条件？在温度为53（℉）时，预测O 形环损坏的数量；要求O 形环损坏的数量小于1，需要温度满足什么条件？

（1）建立Logistic回归模型

由于表5-2提供的数据只是在一定温度条件下O 形环损坏的数量（它的取值是0，1，2和3），因此可以考虑建立广义线性模型——Logistic回归模型．

在每个发射过程中，O 形环损坏的数量服从参数为p 和n＝6 的二项分布binomial（p，6）．其中，参数p（O 形环损坏的概率）是温度（T）的函数，其连接函数为

pagenumber_ebook=101,pagenumber_book=92

我们建立Logistic回归模型如下：

以下根据表5-2的数据对模型（5．3．2）进行参数估计和检验，其代码如下：

pagenumber_ebook=101,pagenumber_book=92

结果如下：

pagenumber_ebook=101,pagenumber_book=92

根据以上结果，可以看出模型已经通过了检验，得到的Logistic回归方程为

所以有

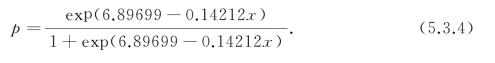
pagenumber_ebook=102,pagenumber_book=93

（2）以下在温度为53（℉）时，预测O 形环损坏的概率

当温度为53（℉）时，根据式（5．3．4），则O 形环损坏的概率为

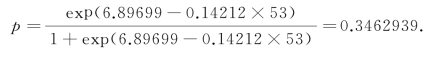
pagenumber_ebook=102,pagenumber_book=93

（3）要使O 形环损坏的概率小于0．05，温度需要满足的条件

设x 为温度（℉），根据式（5．3．4），要使O 形环损坏的概率小于0．05，即 pagenumber_ebook=102,pagenumber_book=93 ＜0．05，解此不等式，得x＞69．24732（℉）．(www.chuimin.cn)

（4）建立对数线性模型

由于表5-2提供的数据只是在一定温度条件下O 形环损坏的数量（它的取值是0，1，2和3），因此可以考虑建立广义线性模型——对数线性模型．

在每个发射过程中O 形环损坏的数量服从泊松分布P（y），其中y（O 形环损坏的数量）是x（温度）的函数，则对数线性回归方程为

以下根据表5-2的数据对模型（5．3．5）进行参数估计和检验，其代码如下：

pagenumber_ebook=102,pagenumber_book=93

结果如下：

pagenumber_ebook=102,pagenumber_book=93

pagenumber_ebook=103,pagenumber_book=94

根据以上结果，可以看出模型已经通过了检验，得到的方程为

所以有

（5）在温度为53（℉）时，预测O 形环损坏的数量

当温度为53（℉）时，根据模型（5．3．7），则O 形环损坏的数量为

exp(4．28008－0．08008×53)＝1．03649≈1．

（6）要求O 形环损坏的数量小于1，温度需要满足的条件

根据模型（5．3．7），有

y＝exp（4．28008－0．08008x）＜1，ln[exp（4．28008－0．08008x）]＜0，4．28008－0．08008x＜0，由此得到x＞53．44755（℉）．

延伸阅读——“挑战者号”发射前发生了什么？

“挑战者号”最初计划于美国东部时间1月22日下午2时43分在佛罗里达州的肯尼迪航天中心（KSC）发射，但是，由于上一次任务STS-61-C的延迟导致发射日推后到23日，然后是24日．接着又因为塞内加尔达喀尔的越洋中辍降落（TAL）场地的恶劣天气，发射又推迟到了25日．NASA 决定使用达尔贝达作为TAL 场地，但由于该场地的配备无法应对夜间降落，发射又不得不被改到佛罗里达时间的清晨．而又根据预报，KSC 当时的天气情况不宜发射，发射再次推后到美国东部时间27日上午9时37分．由于外部舱门通道的问题，发射又推迟了一天．首先，一个用于校验舱门密封安全性的微动开关指示器出现了故障．然后，一个坏掉的门闩使工作人员无法从航天飞机的舱门上取下闭合装置器．当工作人员最终把装置器锯下之后，航天飞机着陆跑道上的侧风超过了进行返回着陆场地（RTLS）中断的极限．直到发射时限用尽，并开始采用备用计划时，侧风才停了下来．

天气预报称28日的清晨将会非常寒冷，气温接近华氏31度（摄氏－0．5度），这是允许发射的最低温度．过低的温度让莫顿·塞奥科公司的工程师感到担心，该公司是制造与维护航天飞机SRB部件的承包商．在27日晚间的一次远程会议上，塞奥科公司的工程师和管理层同来自肯尼迪航天中心和马歇尔航天飞行中心的NASA 管理层讨论了天气问题．部分工程师，如比较著名的罗杰·博伊斯乔利，再次表达了他们对密封SRB部件接缝处的O 形环的担心：低温会导致O 形环的橡胶材料失去弹性．他们认为，如果O 形环的温度低于华氏53度（约摄氏11．7度），将无法保证它能有效密封住接缝．他们也提出，发射前一天夜间的低温，几乎肯定把SRB的温度降到华氏40度的警戒温度以下．但是，莫顿·塞奥科公司的管理层否决了他们的异议，他们认为发射进程能按日程进行．

由于低温，航天飞机旁矗立的定点通信建筑被大量冰雪覆盖．肯尼迪冰雪小组在红外摄像机中发现，右侧SRB部件尾部接缝处的温度仅有华氏8度（摄氏－13度）：从液氧舱通风口吹来的极冷空气降低了接缝处的温度，让该处的温度远低于气温，并远低于O 形环的设计承限温度．但这个信息从未传达给决策层．冰雪小组用了一整夜的时间来移除冰雪；同时，航天飞机的最初承包商罗克韦尔国际公司的工程师，也在表达着他们的担心．他们警告说，发射时被震落的冰雪可能会撞上航天飞机，或者会由于SRB的排气喷射口引发吸入效应．罗克韦尔公司的管理层告诉航天飞机计划的管理人员阿诺德·奥尔德里奇，他们不能完全保证航天飞机安全地发射；但他们也没能提出一个强有力地反对发射的建议．讨论的最终结果是，奥尔德里奇决定将发射时间再推迟一个小时，以让冰雪小组进行另一项检查．在最后一项检查完成，冰雪开始融化时，最终确定“挑战者号”将在美国东部时间当日上午11时38分发射．

挑战者号的事故常是专题研究的案例，例如工程安全、揭弊者的道德规范、沟通与集体决策等．在加拿大和其他一些国家，更是工程师在取得专业执照前必知内容的一部分．对O 形环在低温下将会失效提出警告的工程师罗杰·博伊斯乔利，辞去了他在莫顿·塞奥科公司的工作，并且成为了工作场所道德规范的一位发言人．他认为，由莫顿·塞奥科公司管理层召开的核心会议，及其最后产生关于发射的建议，“是起因于强烈的顾客威逼，而造成了不道德的决策制定”．麻省理工学院、德州农工大学、德克萨斯大学奥斯汀分校、德雷克塞尔大学和马里兰大学等，都将此事故作为一个教学案例．

挑战者号航天飞机O形环失效的统计分析成果

相关推荐