首页理论教育TheChildrenEverBornData的对数线性模型

TheChildrenEverBornData的对数线性模型

2023-11-18 理论教育版权反馈

【摘要】：下面是普林斯顿大学（Princeton University）提供的数据集The Children Ever Born Data．读者也可在网址（http：//iccm．cc/poisson-regression-in-r/）找到其他根据统计分析类型（线性回归、广义线性回归、生存分析等分类）的其他数据集．（1）首先查看该数据集中的变量＞ceb＜－read．table(＂ht tp：//data．p

下面是普林斯顿大学（Princeton University）提供的数据集The Children Ever Born Data．读者也可在网址（http：//iccm．cc/poisson-regression-in-r/）找到其他根据统计分析类型（线性回归、广义线性回归、生存分析等分类）的其他数据集．

（1）首先查看该数据集中的变量

＞ceb＜－read．table(＂ht tp：//data．princeton．edu/wws509/datasets/ceb．dat＂)

＞names(ceb)

[1]＂dur＂＂res＂＂educ＂＂mean＂＂var＂＂n＂＂y＂

变量说明如下：

pagenumber_ebook=96,pagenumber_book=87

（2）对响应变量——育子数作直方图

hist(ceb＄y,breaks＝50,xlab＝＂children ever born＂,main＝＂Distribution of CEB＂)

结果如图5-2所示．

pagenumber_ebook=97,pagenumber_book=88

图5-2　育子数直方图

从图5-2可以清楚看到育子数的偏倚情况（大体上符合泊松分布）．

（3）建立对数线性模型（泊松回归）

＞hist(ceb＄y,breaks＝50,xlab＝＂children ever born＂,main＝＂Distribution of CEB＂)

＞fit＜－glm(y～educ＋res＋dur,offset＝log(n),family＝poisson( ),data＝ceb)

＞summary(fit)

结果如下：

pagenumber_ebook=97,pagenumber_book=88 (www.chuimin.cn)

pagenumber_ebook=98,pagenumber_book=89

（4）为了更好地解释模型参数，将其指数化

＞exp(coef(fit))

结果如下：

pagenumber_ebook=98,pagenumber_book=89

可见随着婚龄的增长，期望的育子数将相应增长；教育程度越高，期望育子数越低；农村预期育子数比城市高等．

对数线性回归（泊松回归）中需要注意过度离势问题．泊松分布中均值与方差相等，当观测到的响应变量实际分布不满足这一点时，对数线性回归（泊松回归）可能会出现这样的问题．这个问题一般原因是缺少解释变量．我们可以用qcc包检验对数线性回归模型（泊松回归）过度离势．

＞require(qcc)

＞qcc．overdispersion．test(ceb＄y,type＝＂poisson＂)

结果如下：

p 值为0，果然该数据存在过度离势的问题，可以用拟泊松（quasi-poisson）模型对数据进行分析．

＞fit2＜－glm(y～educ＋res＋dur,offset＝log(n),family＝quasipoisson( ),data＝ceb)

＞summary(fit2)

结果如下：

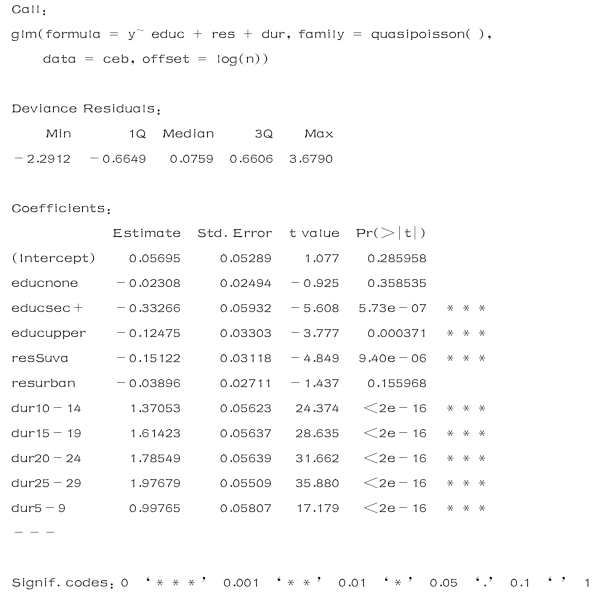
pagenumber_ebook=99,pagenumber_book=90

pagenumber_ebook=100,pagenumber_book=91

比较以上两个模型参数结果，发现参数估计值一致，而t/p 不同．在过度离势的情况下，应采用拟泊松结果的t/p 检验自变量的显著程度．