50名急性淋巴细胞白血病病人，在入院治疗时取得了外猿血中的细胞数x1（千个/mm3），淋巴结浸润等级x2（分为0，1，2，3级），出院后有无巩固治疗x3（1表示有巩固治疗，0 表示无巩固治疗）．通过随访取得病人的生存时间，并用变量y＝0表示生存1年以内，y＝1表示生存1年或1年以上．关于x1，x2，x3 和y 的观测数据，见表5-1．试用Logistic回归模型分析病人生存时间长短的概率与x1，x......
2023-11-18
基于R的实验-Logistic模型
【摘要】：，xp，用向量表示X＝（x1，x2，…，βp 为待估参数．Logistic回归模型中的参数估计常用极大似然估计法得到．设y 是0－1变量，x1，x2，…，n），取P＝πi，P＝1－πi，则yi 的联合概率函数为，yi＝0，1；i＝1，2，…，yn 的似然函数为对数似然函数为对于Logistic回归，将代入，得令＝0，可以用数值计算求待估参数β0，β1，β2，…，βp 的极大似然估计．用R 软件可以解决Logistic回归模型中的参数估计、检验等问题．
在一般线性模型中，因变量y 服从正态分布，当y 服从二项分布（Binomial），即y～b（n，p），针对0－1变量，回归模型须作一些改进．
（1）回归函数应该改用限制在[0，1]区间内的连续曲线，而不能再沿用线性回归方程．应用较多的是Logistic函数（也称Logit变换），其形式为
它的图形呈“S”形，如图5-1所示．
图5-1 S形曲线
（2）因变量yi 本身只取0，1值，不适于直接作为回归模型中的因变量，设p＝P（y＝1），q＝P（y＝0），q＝1－p．假设观测了p 个解释变量x1，x2，…，xp，用向量表示X＝（x1，x2，…，xp）T．与线性模型不同的是，我们不是研究因变量与解释变量之间的关系，而是研究因变量取某些值的概率p 与解释变量之间的关系．实际观测结果表明，概率p 与解释变量之间的关系不是呈线性关系，而是呈“S”形曲线关系．
一般用Logistic曲线来描述概率p 与解释变量之间的关系．
对上式作Logit变换，有
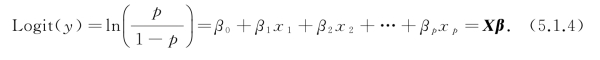(www.chuimin.cn)
式（5．1．4）称为Logistic回归模型，其中β0，β1，β2，…，βp 为待估参数．
Logistic回归模型中的参数估计常用极大似然估计法得到．设y 是0－1变量，x1，x2，…，xp 为与y 相关的变量，对它们的n 次观测数据为（x1，x2，…，xp；yi）（i＝1，2，…，n），取P（yi＝1）＝πi，P（yi＝0）＝1－πi，则yi 的联合概率函数为
，yi＝0，1；i＝1，2，…，n．于是y1，y2，…，yn 的似然函数为
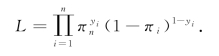
对数似然函数为
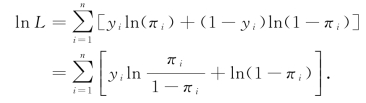
对于Logistic回归，将
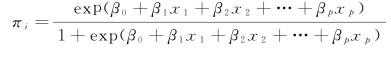
代入，得
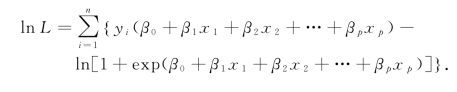
令
＝0，可以用数值计算（改进的Newton-Raphson迭代法等）求待估参数β0，β1，β2，…，βp 的极大似然估计
．用R 软件可以解决Logistic回归模型中的参数估计、检验等问题．
有关应用多元统计分析：基于R的实验的文章
- 详细阅读
-
广义线性模型概述：应用多元统计分析基于R实验详细阅读
，βp的线性函数．因此，对μ 作变换，则可得到下面几种分布的连接函数的形式：正态分布m（μ）＝μ＝∑βi xi．二项分布．Poisson分布m（μ）＝lnμ＝∑βi xi．上述推广体现在以下两个方面：通过一个连接函数，将响应变量的期望与解释变量建立线性关系m[E]＝β0＋β1 x1＋β2 x2＋…......
2023-11-18
-
基于R的实验：iris数据集的聚类分析结果详细阅读
在实验2．3．2中曾对iris数据集进行描述和展示，在实验2．3．4中曾对iris数据集进行可视化．以下将对iris数据集进行进行聚类分析．根据实验2．3．4，我们只知道数据集内有三个品种鸢尾花而不知道每朵花的真正分类，只能凭借花萼及花瓣的长度和宽度分类．以下对鸢尾花iris数据集进行聚类分析，代码如下：＞data(iris);attach(iris)＞iris．hc1＜-hclust(dist(......
2023-11-18
-
基于R的实验：多重比较的均值分析详细阅读
如果F 检验的结论是拒绝H0，则说明因素A 的r 个水平有显著差异，也就是说，r 个均值之间有显著差异．但这并不意味着所有均值之间都有显著差异，这时还需要对每一对μi 和μj 作一一比较．通常采用多重t检验方法进行多重比较．这种方法本质上就是针对每组数据进行t检验，只不过估计方差时利用的是全部数据，因而自由度变大．具体地说，要比较第i组和第j 组均值，即检验H0：μi＝μj,i≠j,i,j＝1,2,…......
2023-11-18
-
一元线性回归回顾-基于R实验详细阅读
回归分析的基本思想和方法以及“回归”名词的由来，要归功于英国统计学家高尔顿（Galton）．高尔顿和他的学生、现代统计学的奠基者之一皮尔逊（Pearson）在研究父母身高与其子女身高的遗传关系时，观察了1 078对夫妇，以每对夫妇的平均身高作为x，而取他们的一个成年儿子的身高作为y，将这些数据画成散点图，发现趋势近似一条直线＝33．73＋0．516x（单位：英寸，1英寸＝2．54 cm）．这表明：......
2023-11-18
-
基于R的实验：城市居民消费性支出聚类分析详细阅读
表7-1给出了我国31个省、市、自治区1999年城镇居民家庭平均每人全年消费支出的8个指标：x1：人均食品支出（元、人）；x2：人均衣着商品支出（元、人）；x3：人均家庭设备用品及服务支出（元、人）；x4：人均医疗保健支出（元、人）；x5：人均交通和通讯支出（元、人）；x6：人均娱乐教育文化服务支出（元、人）；x7：人均居住支出（元、人）；x8：人均杂项商品和服务支出（元、人）．表7-1全国城镇......
2023-11-18
-
基于R的实验：Harman74数据集的因子分详细阅读
Harman74．cor数据集是R 软件自带的数据集，以下对该数据集进行因子分析．（1）查看Harman74数据集中（前面）部分信息Harman74．cor数据集，包含了对芝加哥郊区145名七年级和八年级儿童进行的24 项心理测试指标的相关系数矩阵．其中的24 项心理测试指标包括：VisualPerception，Cubes，PaperFormBoard，Flags，GeneralInformat......
2023-11-18
-
应用多元统计分析方法：基于R实验详细阅读
多元统计分析是统计学中应用性很强的一个分支，它的应用范围十分广泛．多元统计分析可以应用于几乎所有的领域，主要包括经济学、农业、地质学、医学、工业、气象学、金融、精算、物理学、地理学、军事科学、文学、法律、环境科学、考古学、体育科学、遗传学、教育学、生物学、管理科学、水文学等，还有一些交叉学科或方向等．多元统计分析的应用实在是难以一一罗列，以下简要地介绍一下多元统计分析在文学、数据挖掘（作为交叉学科......
2023-11-18
相关推荐