iris数据集是R 自带的数据集,以下对该数据集进行描述和展示.(1)展示iris数据集的前几行>head(iris)结果如下:其中Sepal.Length,Sepal.Width,Petal.Length,Petal.Width,Species,分别表示(鸢尾花)花萼(Sepal)的长度,花萼的宽度,花瓣(Petal)的长度,花瓣的宽度以及每个观测值来自哪一种类.(2)对鸢尾花数据集的数据进行描......
2023-11-18
在实验4.4.1中曾对stackloss数据集进行了逐步回归,在实验4.4.2中曾对stackloss数据集进行了回归诊断.现在我们再考虑进行Box-Cox变换使回归方程的残差满足齐性.
在实验4.4.1中,从回归诊断图(图4-2)的残差图,我们看到了残差图呈喇叭口形状,属于异方差情况,数据需要作Box-Cox变换.
以下进行Box-Cox变换,画3张图:第1张图为残差与预测散点图,第2张图可确定参数λ,第3张图为变换后残差与预测散点图.
>library(MASS)
>op<-par(mfrow=c(3,1),mar=0.4+c(4,4,1,1),oma=c(0,0,2,0))
>plot(fitted(lm.correct),resid(lm.correct),cex=1.2,pch=21,col=ˈredˈ,bg=ˈorangeˈ,xlab=ˈfitted Valueˈ,ylab=ˈResidualsˈ)
>boxcox(lm.correct,lambda=seq(0,2,by=0.1))
>lambda<-0.32
>Ylam<-(stack.loss∧lambda-1)/lambda(www.chuimin.cn)
>lm.lam<-lm(Ylam~Air.Flow+Water.Temp);
>summary(lm.lam)
>plot(fitted(lm.lam),resid(lm.lam),cex=1.2,pch=21,col=ˈblueˈ,bg=ˈorangeˈ,xlab=ˈFitted Valueˈ,ylab=ˈResidualsˈ)
>par(op)
结果如图4-5所示.
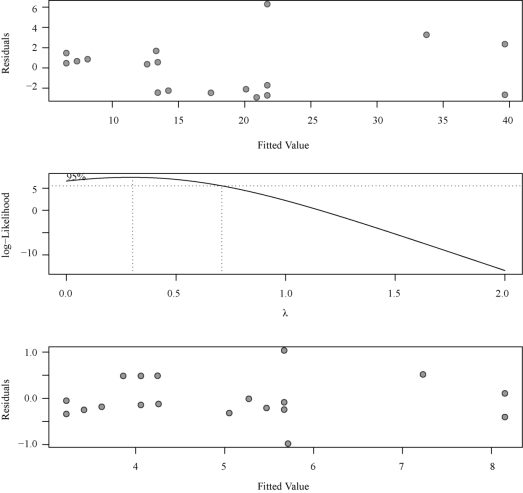
图4-5 B1ox-Cox变换图
比较第1张图和第3张图我们可以看出,变换前后的残差有明显改进.
有关应用多元统计分析:基于R的实验的文章

iris数据集是R 自带的数据集,以下对该数据集进行描述和展示.(1)展示iris数据集的前几行>head(iris)结果如下:其中Sepal.Length,Sepal.Width,Petal.Length,Petal.Width,Species,分别表示(鸢尾花)花萼(Sepal)的长度,花萼的宽度,花瓣(Petal)的长度,花瓣的宽度以及每个观测值来自哪一种类.(2)对鸢尾花数据集的数据进行描......
2023-11-18

,n).记则其中,1p=(1,1,…,pn·)表示对角线元素为p1·,p2·,…,pn· 的对角矩阵.因此,经过变换后所得到的新数据矩阵B,可以看成是由对应矩阵P 经过中心化和标准化后得到的矩阵.设用于检验行与列是否不相关的χ2 统计量为其中,表示第(i,j)单元在检验行与列两个属性变量否不相关时对总χ2 统计量的贡献,有其中,χ2==T[tr]=T[tr]=T[tr],tr表示方阵SQ 的迹.......
2023-11-18

在实验4.4.1中曾对R 自带的stackloss数据集进行了逐步回归,现在我们在实验4.4.1的基础上进行回归诊断.(1)画回归诊断图>opar<-par(mfrow=c(2,2))>plot(lm.step,1:4)>par(opar)结果如图4-2所示.图4-2回归诊断图分析4张回归诊断图(图4-2).第1张是残差图,得到的残差图呈喇叭口形状,属于异方差情况(这样的数据需要作Box-Cox......
2023-11-18

在实验2.3.1中,我们对mtcars数据集进行了展示和描述.在实验2.3.3中,我们对mtcars数据集进行了可视化.现在我们对该数据集中的变量进行回归分析.(1)不考虑变量交互项对该数据集,如果把mpg(汽车每加仑公里数)作为因变量,自变量为hp(马力)和wt(汽车重量)进行回归.>fit<-lm(mpg~hp+wt,data=mtcars)>summary(fit)结果如下:得到的回归方程为......
2023-11-18

在实验2.3.1中,我们对mtcars数据集(R 自带数据集)进行了展示和描述,以下对该数据集进行可视化.(1)汽车每加仑英里数直方图>hist(mtcars$mpg,breaks=10)结果如图2-1所示.(2)按汽缸数划分的各车型车重的核密度图>par(lwd=2)>library(sm)>cyl.f<-factor(mtcars$cyl,levels=c(4,6,8),labels=c("4......
2023-11-18

对R 自带的stackloss数据集进行逐步回归.(1)首先显示stackloss数据集的信息其中,变量为stack.loss(氨气损失百分比),Air.Flow(空气流量),Water.Temp(水温),Acid.Conc.(硝酸浓度).(2)计算变量间的相关性——相关系数>cor(stackloss)结果如下:(3)散布图矩阵>library(car)>scatterplotMatrix(st......
2023-11-18

在实验2.3.2中曾对iris数据集进行描述和展示,在实验2.3.4中曾对iris数据集进行可视化,在实验7.4.1中曾对iris数据集进行聚类分析.通过实验2.3.2对iris数据集进行描述和展示,我们知道iris数据集是对3个品种(species)鸢尾花:setosa、versicolor和virginica各抽取一个容量为50 的样本,测量其花萼长度(Sepal.Lenth)、花萼宽度(Se......
2023-11-18

ability.cov数据集是R 软件自带的数据集,以下对该数据集进行因子分析.(1)查看ability.cov数据集中的信息ability.cov数据集提供了Ability and Intelligence Tests(能力和智力测试)中,112个人参加的六个测试指标general(普通),picture(画图),blocks(积木),maze(迷津),reading(阅读),vocab(词汇)......
2023-11-18
相关推荐