对R 自带的stackloss数据集进行逐步回归．（1）首先显示stackloss数据集的信息其中，变量为stack．loss（氨气损失百分比），Air．Flow（空气流量），Water．Temp（水温），Acid．Conc．（硝酸浓度）．（2）计算变量间的相关性——相关系数＞cor(stackloss)结果如下：（3）散布图矩阵＞library(car)＞scatterplotMatrix(st......
2023-11-18
实验4．4．3state．x77数据集的逐步回归和回归诊断
【摘要】：在实验3．3．3中我们已经研究过美国各州犯罪率与其他因素关系（state．x77数据集），在进行多元线性回归分析中，4个自变量都进入方程时，回归方程的显著性没能通过检验．以下对state．x77数据集进行逐步回归和回归诊断．（1）回顾简单多元线性回归情形＞states＜－as．data．frame(state．x77)＞lm．sol＜－lm(states＄Murder～states＄Populat
在实验3．3．3中我们已经研究过美国各州犯罪率与其他因素关系（state．x77数据集），在进行多元线性回归分析中，4个自变量都进入方程时，回归方程的显著性没能通过检验．以下对state．x77数据集进行逐步回归和回归诊断．
（1）回顾简单多元线性回归情形
＞states＜－as．data．frame(state．x77)
＞lm．sol＜－lm(states＄Murder～states＄Population＋states＄Income＋states＄Illiteracy＋states＄Frost)
＞summary(lm．sol)
结果如下：
从上面的结果来看，以上4 个自变量都进入回归方程时，显著性没能通过检验．
（2）用“step（ ）”函数进行逐步回归
对AIC进行观察，尽可能地使AIC达到最小，以此往复直到建立更合理与简单实用的回归模型．
＞lm．step＜－step(lm．sol)
结果如下：
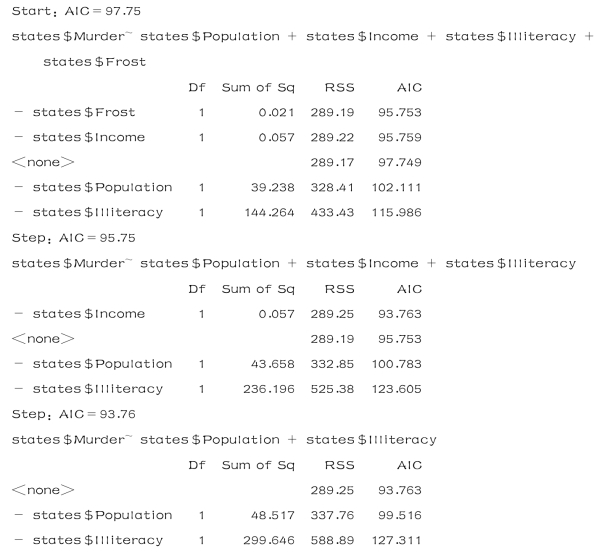
从以上运行结果看，首先通过AIC 值的大小，删除了变量Frost，接着删除了变量Income，继续进行了回归分析．当用四个自变量作回归时，AIC值为97．75，如果去掉变量Frost，则相应的AIC值为95．75，如果再去掉变量Income，可以使AIC值达到最小，相应的AIC值为93．76．
提取逐步回归的相关信息：
＞summary(lm．step)
结果如下：
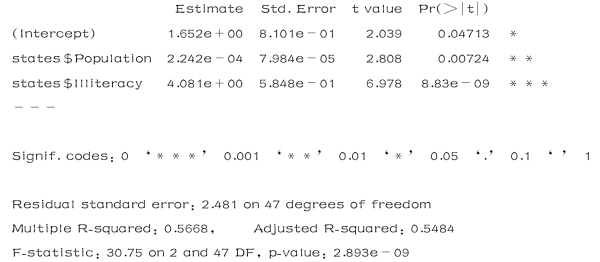
从结果看，回归系数检验的显著性水平有了较大的提高，但Multiple Rsquared：0．5668仍然不理想，结果还有待改进．
（3）进行回归诊断
＞influence．measures(lm．step)
结果如下：
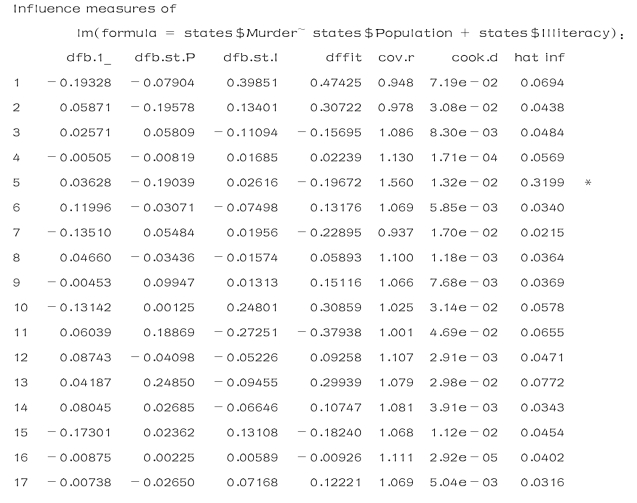
分析回归诊断的结果：第6 列为Cook 距离，第7 列为帽子值（也称高杠杆值），最后一列为影响点记号．由上面的结果得到5，18，24，28，32和43号点是强影响点（inf为∗）．(www.chuimin.cn)
以下画回归诊断图：
＞op＜－par(mfrow＝c(2,2),mar＝0．4＋c(4,4,1,1),oma＝c(0,0,2,0))
＞plot(lm．step,1：4)
＞par(op)
结果如图4-3所示．
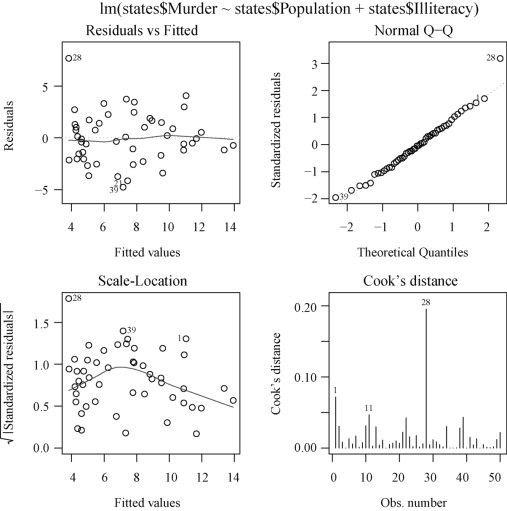
图4-3 回归诊断图
分析4张回归诊断图（图4-3）．第1张是残差图，得到的残差图有些呈喇叭口形状，可能属于异方差情况，这样的数据需要作Box-Cox 变换．第2 张图是正态QQ 图，除28号点外，基本上都在一条直线上，也就是说，除28号点外，残差满足正态性．第3张图是标准差的平方根与预测值的散点图，28号点的值大于1．5，这说明28号点是异常值点（在95%的范围外）．第4张图给出了Cook距离，从图上来看，28 号点的Cook 距离最大，这说明28 号点可能是强影响点（高杠杆点）．
从图4-3可以看出，28号点是异常值点，把它剔除后，再来看回归的效果：
＞n＜－length(states＄Population)
＞weights＜－rep(1,n)
＞lm．correct＜－lm(states＄Murder～states＄Population＋states＄Illiteracy,subset＝－28,weights＝weights)
＞summary(lm．correct)
结果如下：
再画回归诊断图：
＞op＜－par(mfrow＝c(2,2),mar＝0．4＋c(4,4,1,1),oma＝c(0,0,2,0))
＞plot(lm．correct,1：4)
＞par(op)
结果如图4-4所示．
从图4-4与图4-3的比较可以看出，剔除28 号点后回归诊断的效果要好一些．
我们再来分析回归诊断图（图4-4）．这里共4张图，其中第1张是残差图，我们看到的残差图基本上是均匀的，这样的数据不需要作Box-Cox变换．
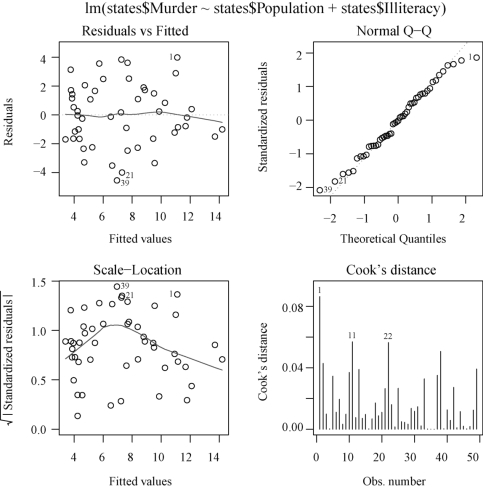
图4-4 回归诊断图
有关应用多元统计分析：基于R的实验的文章
- 详细阅读
-
多元回归分析：R语言中stackloss数据详细阅读
在实验4．4．1中曾对R 自带的stackloss数据集进行了逐步回归，现在我们在实验4．4．1的基础上进行回归诊断．（1）画回归诊断图＞opar＜－par(mfrow＝c(2,2))＞plot(lm．step,1：4)＞par(opar)结果如图4-2所示．图4-2回归诊断图分析4张回归诊断图（图4-2）．第1张是残差图，得到的残差图呈喇叭口形状，属于异方差情况（这样的数据需要作Box-Cox......
2023-11-18
-
Boston数据集的回归分析详细阅读
MASS包中包含Boston数据集（波士顿房价），它记录了波士顿周围506个街区的medv（房价中位数）．我们将设法用13个预测变量如rm（每栋住宅的平均房间数），age（平均房龄），lstat（社会经济地位低的家庭所占比例）等来预测medv（房价中位数）．（1）首先查看Boston数据集（波士顿房价）中的变量＞library(MASS)＞fix(Boston)＞names(Boston)结果如下......
2023-11-18
-
多元统计分析：R实验中的mtcars数据集回详细阅读
在实验2．3．1中，我们对mtcars数据集进行了展示和描述．在实验2．3．3中，我们对mtcars数据集进行了可视化．现在我们对该数据集中的变量进行回归分析．（1）不考虑变量交互项对该数据集，如果把mpg（汽车每加仑公里数）作为因变量，自变量为hp（马力）和wt（汽车重量）进行回归．＞fit＜－lm(mpg～hp＋wt,data＝mtcars)＞summary(fit)结果如下：得到的回归方程为......
2023-11-18
-
回归分析与state.x77数据集详细阅读
R 中自带的state．x77数据集包括Population（人口），Income（收入），Murder（犯罪率），Frost（结霜天数），Illiteracy（文盲率），Area（土地面积），Life．Exp（预期寿命）及HS Grad（高中毕业率）8个变量．以下我们考虑（美国各州的）Murder（犯罪率）与一些因素的关系，这些因素主要包括：Population（人口），Income（收入），I......
2023-11-18
-
利用WisconsinBreastCance详细阅读
Wisconsin Breast Cancer数据集有699条记录，每条记录都是记录一位胸部有肿瘤的病人的特征数据。可以从中随机选择444条良性记录和39条恶性记录组成一数据集。文献[107]描述的是基于聚类的且基于密度局部特异数据挖掘方法—FindCBLOF，在Wisconsin Breast Cancer Data上的实验结果显示了其挖掘特异数据的能力在同类算法中是优越的。结果再次表明Cpecu Find挖掘特异数据的能力略优于pecu Find。表3.4Wisconsin Breast Cancer数据集上的实验结果比较......
2023-06-16
-
实验caith数据集的对应分析详细阅读
在R 软件中，有个MASS包，其中有一个caith数据集，是关于眼睛颜色和头发颜色的数据．（1）查看caith数据集的信息＞library(MASS)＞caith结果如下：从以上结果可以看出，caith数据集中眼睛颜色：blue，light，medium 和dark；头发颜色：fair，red，medium，dark和black．（2）进行χ2 检验——考察行变量和列变量是否独立＞chisq．te......
2023-11-18
-
基于R的实验：iris数据集的聚类分析结果详细阅读
在实验2．3．2中曾对iris数据集进行描述和展示，在实验2．3．4中曾对iris数据集进行可视化．以下将对iris数据集进行进行聚类分析．根据实验2．3．4，我们只知道数据集内有三个品种鸢尾花而不知道每朵花的真正分类，只能凭借花萼及花瓣的长度和宽度分类．以下对鸢尾花iris数据集进行聚类分析，代码如下：＞data(iris);attach(iris)＞iris．hc1＜-hclust(dist(......
2023-11-18
相关推荐