R 中自带的state．x77数据集包括Population（人口），Income（收入），Murder（犯罪率），Frost（结霜天数），Illiteracy（文盲率），Area（土地面积），Life．Exp（预期寿命）及HS Grad（高中毕业率）8个变量．以下我们考虑（美国各州的）Murder（犯罪率）与一些因素的关系，这些因素主要包括：Population（人口），Income（收入），I......
2023-11-18
Boston数据集的回归分析
【摘要】：MASS包中包含Boston数据集（波士顿房价），它记录了波士顿周围506个街区的medv（房价中位数）．我们将设法用13个预测变量如rm（每栋住宅的平均房间数），age（平均房龄），lstat（社会经济地位低的家庭所占比例）等来预测medv（房价中位数）．（1）首先查看Boston数据集（波士顿房价）中的变量＞library(MASS)＞fix(Boston)＞names(Boston)结果如下
MASS包中包含Boston数据集（波士顿房价），它记录了波士顿周围506个街区的medv（房价中位数）．我们将设法用13个预测变量如rm（每栋住宅的平均房间数），age（平均房龄），lstat（社会经济地位低的家庭所占比例）等来预测medv（房价中位数）．
（1）首先查看Boston数据集（波士顿房价）中的变量
＞library(MASS)
＞fix(Boston)
＞names(Boston)
结果如下：
[1]＂c rim＂ ＂zn＂ ＂indus＂ ＂chas＂ ＂nox＂ ＂rm＂ ＂age＂
[8]＂dis＂ ＂rad＂ ＂tax＂ ＂pt ratio＂ ＂black＂ ＂lstat＂ ＂medv＂
想要了解该数据集的更多信息，可以输入“？？Boston”．
（2）用“lm（ ）”函数拟合简单线性回归模型，将medv作为因变量，lstat作为自变量
首先绑定Boston数据集，
＞lm．fit＝lm(medv～lstat,data＝Boston)
＞attach(Boston)
＞lm．fit＝lm(medv～lstat)
如果输入“lm．fit”，则会输出一些基本信息．
＞lm．fit
结果如下：
用summary（lm．fit）了解更多信息．
＞summary(lm．fit)
结果如下：
为了得到系数估计值的置信区间，可以用“confint（ ）”函数．
＞confint(lm．fit)
结果如下：
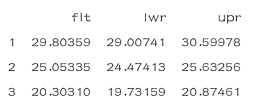
根据lstat的值预测medv 时，可用“predict（ ）”函数计算置信区间和预测区间．
＞predict(lm．fit,data．frame(lstat＝(c(5,10,15))),
＋interval＝＂confidence＂)
结果如下：
＞predict(lm．fit,data．frame(lstat＝(c(5,10,15))),
＋interval＝＂prediction＂)
结果如下：
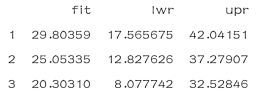
如果lstat＝10，则相应的0．95置信区间为（24．47413，25．63256），相应的0．95预测区间为（12．827626，37．27907）．置信区间和预测区间有相同的中心点．如果lstat＝10，则medv的预测值为25．05335．
以下画medv和lstat散点图以及回归直线：
＞plot(lstat,medv)
＞abline(lm．fit)(www.chuimin.cn)
结果如图3-4所示．
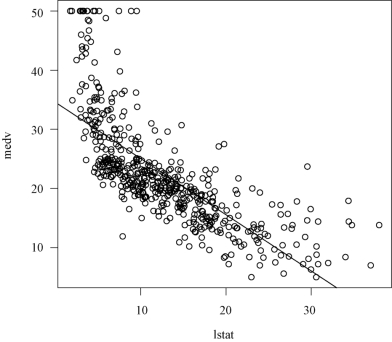
图3-4 medv和lstat散点图以及回归直线
（3）用medv作为因变量，建立lstat和lstat2的多项式回归
在（2）中，我们用medv作为因变量，lstat作为自变量，进行简单线性回归．现在我们用medv作为因变量，建立lstat和lstat2的多项式回归．
＞lm．fit2＝lm(medv～lstat＋I(lstat∧2),data＝Boston)
＞summary(lm．fit2)
结果如下：
通过与（2）进行比较，我们发现增加lstat2使模型比只有lstat作为自变量的模型得到了改进．
（4）用medv作为因变量，建立lstat的（高次）多项式回归
要创建一个三次多项式拟合，我们可以向模型加入lstat3作为自变量．然而，这种方法对于高阶多项式就会变得繁琐．更好的方法是用“poly（ ）”和“lm（ ）”函数创建多项式．例如，下面产生一个5阶多项式拟合：
＞lm．fit5＝lm(medv～poly(lstat,5),data＝Boston)
＞summary(lm．fit5)
结果如下：
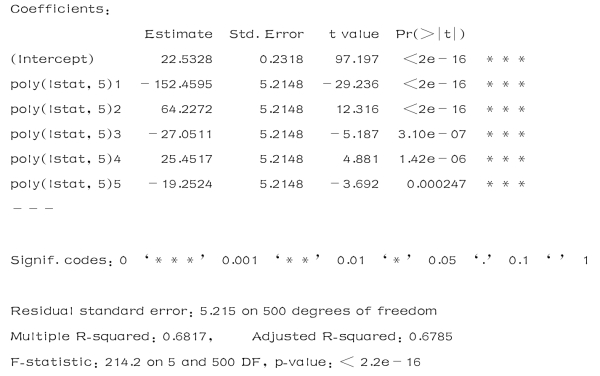
以上结果表明，在模型中加入5阶以下的多项式改善了模型拟合．然而，进一步考察表明，5阶以上的多项式在回归拟合中的p 值并不显著．
（5）用medv作为因变量，建立lstat和age的回归模型
在前面我们用medv作为因变量，lstat作为自变量，进行简单线性回归．现在用medv作为因变量，自变量为lstat和age，继续进行回归分析．
＞lm．fit＝lm(medv～lstat＋age,data＝Boston)
＞summary(lm．fit)
结果如下：
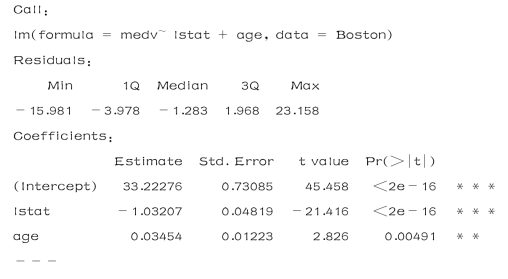
（6）用medv作为因变量，数据集中全部13个自变量，继续进行回归分析
Boston（波斯顿房价）数据集包含13个自变量，用所有自变量进行回归（一一输入会麻烦，可以用如下的快捷方法）．
＞lm．fit＝lm(medv～．,data＝Boston)
＞summary(lm．fit)
结果如下：
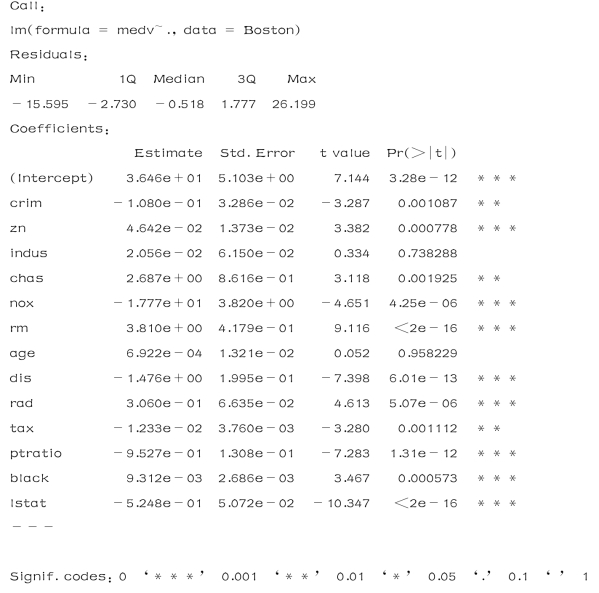
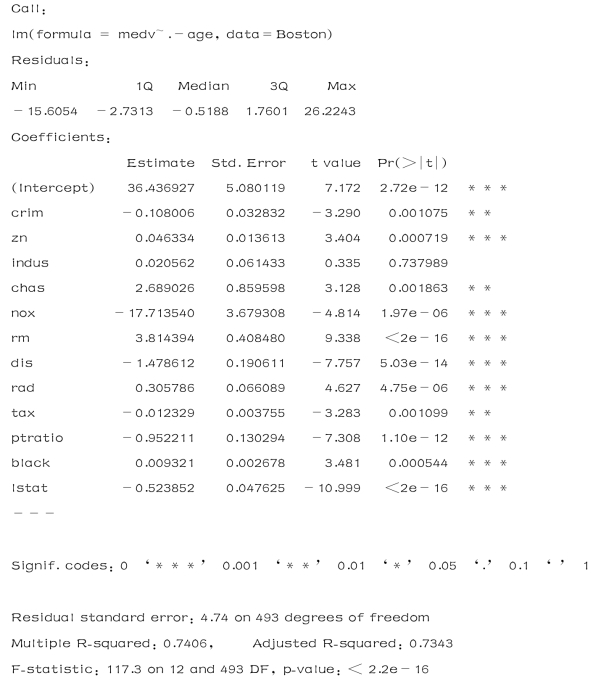
如果想用除某一个变量之外所有其他自变量进行回归分析，例如在上面的回归结果中，age变量有很高的p 值（0．958229），可以用如下进行：
＞lm．fit＝lm(medv～．－age,data＝Boston)
＞summary(lm．fit)
结果如下：
有关应用多元统计分析：基于R的实验的文章
- 详细阅读
-
多元回归分析：R语言中stackloss数据详细阅读
在实验4．4．1中曾对R 自带的stackloss数据集进行了逐步回归，现在我们在实验4．4．1的基础上进行回归诊断．（1）画回归诊断图＞opar＜－par(mfrow＝c(2,2))＞plot(lm．step,1：4)＞par(opar)结果如图4-2所示．图4-2回归诊断图分析4张回归诊断图（图4-2）．第1张是残差图，得到的残差图呈喇叭口形状，属于异方差情况（这样的数据需要作Box-Cox......
2023-11-18
-
多元统计分析：R实验中的mtcars数据集回详细阅读
在实验2．3．1中，我们对mtcars数据集进行了展示和描述．在实验2．3．3中，我们对mtcars数据集进行了可视化．现在我们对该数据集中的变量进行回归分析．（1）不考虑变量交互项对该数据集，如果把mpg（汽车每加仑公里数）作为因变量，自变量为hp（马力）和wt（汽车重量）进行回归．＞fit＜－lm(mpg～hp＋wt,data＝mtcars)＞summary(fit)结果如下：得到的回归方程为......
2023-11-18
-
实验4．4．3state．x77数据集的逐步详细阅读
在实验3．3．3中我们已经研究过美国各州犯罪率与其他因素关系（state．x77数据集），在进行多元线性回归分析中，4个自变量都进入方程时，回归方程的显著性没能通过检验．以下对state．x77数据集进行逐步回归和回归诊断．（1）回顾简单多元线性回归情形＞states＜－as．data．frame(state．x77)＞lm．sol＜－lm(states＄Murder～states＄Populat......
2023-11-18
-
生态数据分析与建模：直线回归分析的计算详细阅读
直线回归是回归分析中最简单的一种，又称为简单回归。（一）直线回归方程散点图上呈现直线趋势的两个变数，自变量x的每一个取值都有y的一个分布与之对应。试计算其直线回归方程。为简化手续，可从以下恒等式得出：（五）直线回归的数学模型和基本假定回归分析的依据是直线回归模型。......
2023-11-17
-
基于R的实验stackloss数据集逐步回归详细阅读
对R 自带的stackloss数据集进行逐步回归．（1）首先显示stackloss数据集的信息其中，变量为stack．loss（氨气损失百分比），Air．Flow（空气流量），Water．Temp（水温），Acid．Conc．（硝酸浓度）．（2）计算变量间的相关性——相关系数＞cor(stackloss)结果如下：（3）散布图矩阵＞library(car)＞scatterplotMatrix(st......
2023-11-18
-
生态数据分析：多元线性回归详细阅读
式（7-1）就是多元线性回归的数字模型。（二）建立多元线性回归方程设y对x1，x2，…，m）称为高斯乘数，是多元线性回归分析假设检验与进一步统计分析所需要的。建立产量y与穗数x1、每穗粒数x2的二元线性回归方程。如果此回归关系是真实的，则可依据该二元线性回归方程由穗数x1、每穗粒数x2预测和控制产量y。统计学已证明，在m元线性回归分析中，离回归平方和的自由度为。......
2023-11-17
-
生态数据分析：多元线性回归的假设检验详细阅读
，βm不全为零在H0成立条件下，有由上述统计数F进行F检验即可推断多元线性回归关系的显著性。［例6］对［例5］所建立的二元线性回归方程进行假设检验。表7-2二元线性回归方差分析表二、偏回归系数的假设检验上述多元线性回归关系假设检验是检验各自变量共同对因变量的线性影响是否显著。因此，当多元线性回归关系显著时，还必须逐一对各个偏回归系数进行假设检验，发现并剔除对因变量的线性影响不显著的自变量。......
2023-11-17
相关推荐