首页理论教育多元统计分析：用R进行回归分析

多元统计分析：用R进行回归分析

2023-11-18 理论教育版权反馈

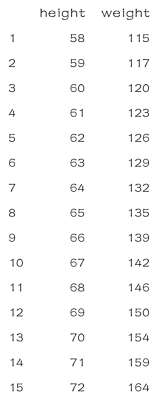
【摘要】：women数据集（R 自带数据集）提供了15个年龄在30～39岁之间女性的身高和体重的信息．（1）查看women数据集（身高和体重）的信息＞women结果如下：（2）weight和height的简单线性回归＞fit＜－lm(weight～height,data＝women)＞summary(fit)结果如下：由此得到的回归方程为从以上结果可以看出，回归方程通过检验．（3）身高和体重的散点图以及回归

women数据集（R 自带数据集）提供了15个年龄在30～39岁之间女性的身高和体重的信息．

（1）查看women数据集（身高和体重）的信息

＞women

结果如下：

pagenumber_ebook=52,pagenumber_book=43

（2）weight和height的简单线性回归

＞fit＜－lm(weight～height,data＝women)

＞summary(fit)

结果如下：

pagenumber_ebook=52,pagenumber_book=43

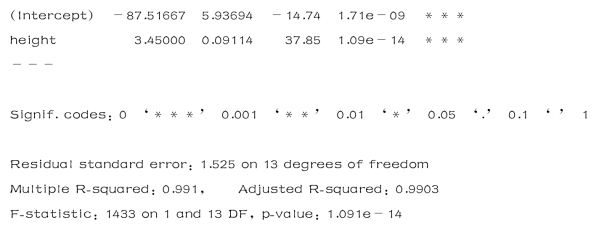
pagenumber_ebook=53,pagenumber_book=44

由此得到的回归方程为

从以上结果可以看出，回归方程通过检验．

（3）身高和体重的散点图以及回归直线

＞plot(women＄height,women＄weight)

＞abline(fit)

结果如图3-1所示．

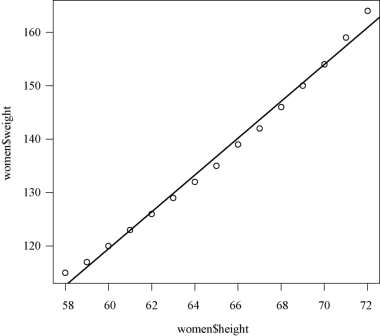
pagenumber_ebook=53,pagenumber_book=44

图3-1　身高和体重的散点图以及回归直线

从图3-1可以看出，15个数据点在一条直线附近．

（4）添加一个身高的平方项

添加一个身高的平方项来提高回归的精度．用I（x∧2）创建变量x2（函数“I（）”是必要的，因为“∧”在公式中有特殊的含义．

I（height∧2）表示添加一个身高的平方项．

＞fit2＜－lm(weight～height＋I(height∧2),data＝women)

＞summary(fit2)

结果如下：

pagenumber_ebook=54,pagenumber_book=45

由此得到的回归方程为

(www.chuimin.cn)

从以上结果可以看出，回归方程通过检验．

（5）身高和体重的散点图及其二次回归

＞plot(women＄height,women＄weight)

＞lines(women＄height,fitted(fit2))

结果如图3-2所示．

从图3-2中，可以看到二次回归曲线拟合效果比线性好．

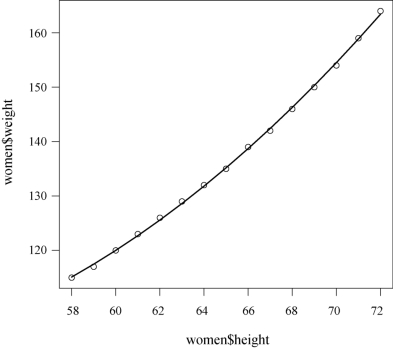
pagenumber_ebook=55,pagenumber_book=46

图3-2　身高和体重的散点图及其二次回归曲线

（6）添加一个身高的三次项

I（height∧3）表示添加一个身高的三次项．

＞fit3＜－lm(weight～height＋I(height∧2)＋I(height∧3),data＝women)

＞summary(fit3)

结果如下：

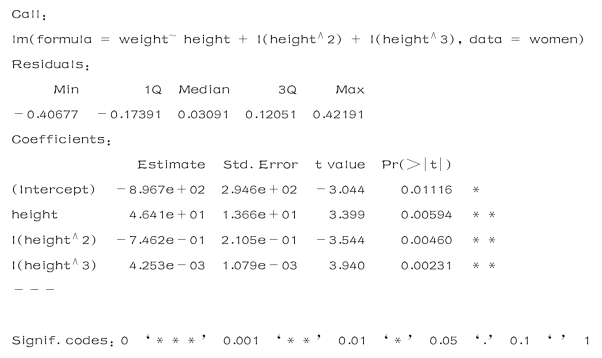
pagenumber_ebook=55,pagenumber_book=46

pagenumber_ebook=56,pagenumber_book=47

（7）身高和体重的散点图及其三次回归

以下调用car包中的“scatterplot（）”函数，画身高和体重的散点图及其三次回归：

＞library(car)

＞scatterplot(weight～height,data＝women,

＋spreed＝FALSE,lty．smooth＝2,

＋pch＝19,

＋main＝＂women Age 30－39＂,

＋xlab＝＂height(lnches)＂,

＋ylab＝＂weight(lbs．)＂)

结果如图3-3所示．

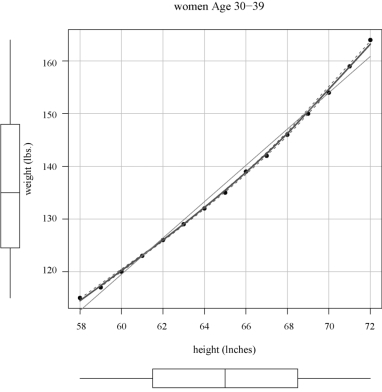
pagenumber_ebook=56,pagenumber_book=47

图3-3　身高和体重的散点图及其三次回归曲线

在图3-3中，边界为箱线图．从图3-3中，可以看到三次回归曲线拟合效果比线性更好．