利用R进行多元统计分析实验，可视化iris数据集

2023-11-18 理论教育版权反馈

【摘要】：在实验2．3．2中对iris数据集进行了描述和展示，以下对iris数据集进行可视化．花萼长度、花萼宽度、花瓣长度、花瓣宽度的小提琴图小提琴图是箱线图的变种，因为形状酷似小提琴而得名．小提琴图是将箱线图与核密度图结合在一起，它在箱线图上以镜像方式叠加上核密度图．绘制小提琴图，可以使用vioplot包中的“vioplot（）”函数，但在第一次使用之前请先安装vioplot包．“vioplot（）”函数的调用格式为：vioplot（x1，x2，…

在实验2．3．2中对iris数据集（R 自带数据集）进行了描述和展示，以下对iris数据集进行可视化．

（1）花萼长度、花萼宽度、花瓣长度、花瓣宽度的小提琴图

小提琴图（violin plot）是箱线图（box plot）的变种，因为形状酷似小提琴而得名．小提琴图是将箱线图与核密度图结合在一起，它在箱线图上以镜像方式叠加上核密度图．

绘制小提琴图，可以使用vioplot包中的“vioplot（）”函数，但在第一次使用之前请先安装vioplot包．“vioplot（）”函数的调用格式为：vioplot（x1，x2，…，names，col），其中：x1，x2，…表示要绘制的一个或多个数值向量（将为每个向量绘制一幅小提琴图），names是小提琴图中标签的字符向量，col是一个为每幅小提琴图指定颜色的向量．

＞install．packages(＂vioplot＂)

＞library(vioplot)

＞count＜－table(iris＄Species)

＞par(mfrow＝c(2,2))

＞x1＜－iris＄Sepal．Length[iris＄Species＝＝＂setosa＂]

＞x2＜－iris＄Sepal．Length[iris＄Species＝＝＂versicolor＂]

＞x3＜－iris＄Sepal．Length[iris＄Species＝＝＂virginica＂]

＞vioplot(x1,x2,x3,col＝＂gold＂,names＝c(＂setosa＂,＂versicolor＂,＂virginica＂))

＞title(＂Sepal．Length＂,xlab＝＂Species＂,ylab＝＂Length＂)

＞vioplot(x1,x2,x3,col＝＂gold＂,names＝c(＂setosa＂,＂versicolor＂,＂virginica＂))

＞title(＂Sepal．Width＂,xlab＝＂Species＂,ylab＝＂Width＂)

＞vioplot(x1,x2,x3,col＝＂gold＂,names＝c(＂setosa＂,＂versicolor＂,＂virginica＂))

＞title(＂Petal．Length＂,xlab＝＂Species＂,ylab＝＂Length＂)

＞vioplot(x1,x2,x3,col＝＂gold＂,names＝c(＂setosa＂,＂versicolor＂,＂virginica＂))

＞title(＂Petal．Width＂,xlab＝＂Species＂,ylab＝＂Width＂)

结果如图2-6所示．

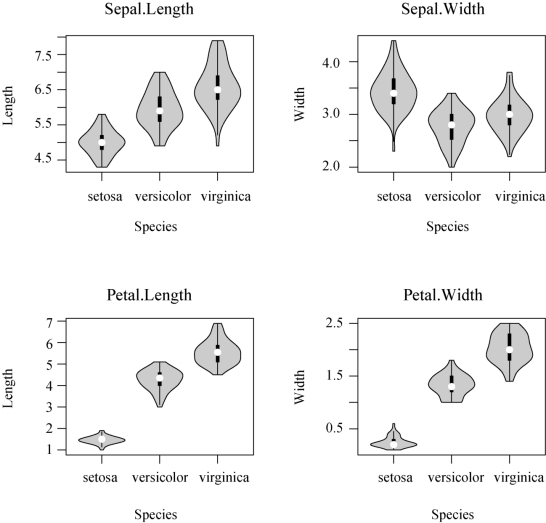
pagenumber_ebook=28,pagenumber_book=19

图2-6　花萼长度、花萼宽度、花瓣长度、花瓣宽度的小提琴图

在图2-6中，白点是中位数，黑色盒子的范围是下4分位数（25%分位数）到上4分位数（75%分位数），细黑线表示虚线，外部形状为核密度估计．Sepal．Length，Sepal．Width，Petal．Length，Petal．Width，分别表示花萼的长度，花萼的宽度，花瓣的长度，花瓣的宽度．

（2）四个变量的频数直方图

＞oldpar＜－par(mfcol＝c(2,2))

＞titles＜－names(iris)[1：4]

＞for(i in 1：4){

＋hist(x＝iris[,i],main＝paste(＂Histogram of＂,titles[i]),xlab＝titles[i])}

＞par(oldpar)

结果如图2-7所示．

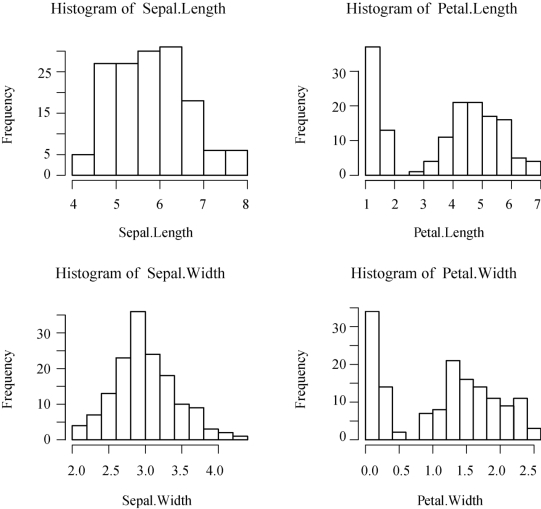
pagenumber_ebook=29,pagenumber_book=20

图2-7　鸢尾花四个变量的频数直方图

从图2-7可以看出，除了花萼的宽度（Sepal．Width）外，其他几个变量的频数直方图都是有偏的，这对了解整体特征是很有帮助的．

（3）带核密度的四个变量的频率直方图

＞oldpar＜－par(mfcol＝c(2,2))

＞titles＜－names(iris)[1：4]

＞for(i in 1：4){

＋hist(x＝iris[,i],main＝paste(＂Histogram of＂,titles[i]),

＋xlab＝titles[i],probability＝TRUE)

＋lines(density(x＝iris[,i]))

＋rug(jit ter(x＝iris[,i]))

＋}

＞par(oldpar)

结果如图2-8所示．

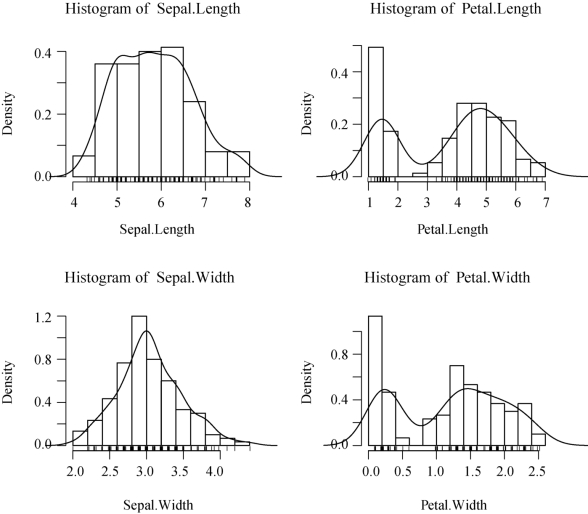
pagenumber_ebook=30,pagenumber_book=21

图2-8　鸢尾花带核密度的四个变量的频率直方图

从图2-8可以看出，花萼的宽度（Sepal．Width）和正态分布比较接近．

（4）花萼宽度的QQ 图

为了确定花萼的宽度是否满足正态分布，这里用QQ 图来检验．

＞attach(Sepal．Width)

＞qqnorm(Sepal．Width);qqline(Sepal．Width)

结果如图2-9所示．

pagenumber_ebook=31,pagenumber_book=22

图2-9　花萼宽度的QQ 图

从图2-9可以看出，除了末尾的观测值，大体上还是符合正态分布的．

（5）三种鸢尾花的花萼宽度箱线图、花萼长度箱线图

以下用ggplot2包中的函数“ggplot（）”来画箱线图，但第一次使用前请先安装ggplot2包．(www.chuimin.cn)

＞install．packages(＂ggplot2＂)

＞library(ggplot2)

＞p＜－ggplot(data＝iris,mapping＝aes(x＝Species,y＝Sepal．Width,fill＝Spe-cies))

＞p＋geom_boxplot( )

结果如图2-10所示．

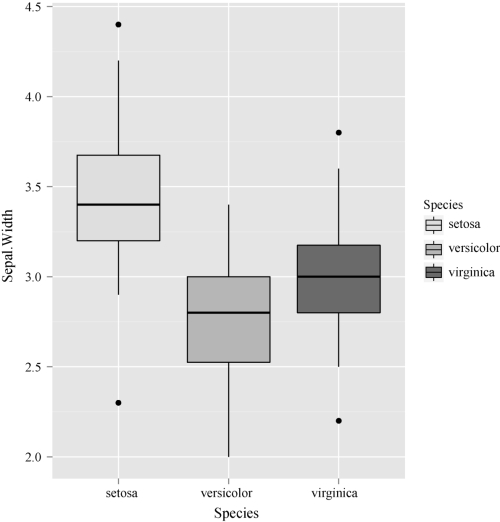
pagenumber_ebook=32,pagenumber_book=23

图2-10　三种鸢尾花的花萼宽度箱线图

从图2-10可以看出，setosa类型的鸢尾花和其他种类的鸢尾花的差别比较明显，而versicolor和virginica这两类虽有差别但并不是很明显．

同样，可以绘制三种鸢尾花的花萼长度箱线图．

＞p＜－ggplot(data＝iris,mapping＝aes(x＝Species,y＝Sepal．Length,fill＝Species))

＞p＋geom_boxplot( )

结果如图2-11所示．

从图2-11可以看出，三种鸢尾花的花萼长度有比较明显的差别．

类似地，可以绘制三种鸢尾花的花瓣宽度箱线图、花瓣长度箱线图，这里从略．

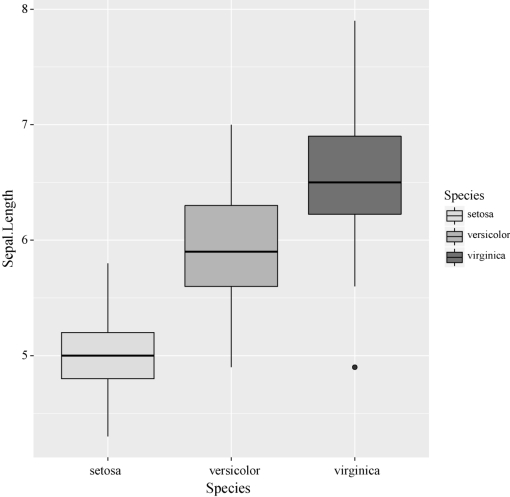
pagenumber_ebook=33,pagenumber_book=24

图2-11　三种鸢尾花的花萼长度箱线图

（6）三种鸢尾花的花萼长度和宽度的散点图（加平滑曲线）

以下通过散点图来进一步了解三种不同鸢尾花的两个变量之间的关系，加平滑曲线的散点图还可以更加清晰地看出两个变量之间的变化趋势．

以下分别绘制三种鸢尾花的花萼长度和宽度的散点图、花瓣长度和宽度的散点图．

＞p＜－ggplot(data＝iris,mapping＝aes(x＝Sepal．Length,y＝Sepal．Width))

＞p＜－p＋geom_point( )＋facet_wrap(facets＝～Species)

＞p＋geom_smooth( )

结果如图2-12所示．

＞p＜－ggplot(data＝iris,mapping＝aes(x＝Petal．Length,y＝Petal．Width))

＞p＜－p＋geom_point( )＋facet_wrap(facets＝～Species)

＞p＋geom_smooth( )

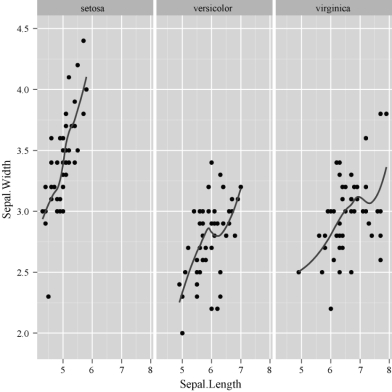
pagenumber_ebook=34,pagenumber_book=25

图2-12　三种鸢尾花的花萼长度和宽度的散点图

结果如图2-13所示．

pagenumber_ebook=34,pagenumber_book=25

图2-13　三种鸢尾花的花瓣长度和宽度的散点图

（7）鸢尾花的三维散点图

图2-12和图2-13分别给出了鸢尾花的二维散点图，以下绘制鸢尾花Sepal．Width（花萼宽度），Petal．Length（花瓣长度），Petal．Width（花瓣宽度）的三维散点图．

绘制三维散点图，可以使用scatterplot3d包中的“scatterplot3d（）”函数，但在第一次使用之前请先安装scatterplot3d包．“scatterplot3d（）”函数的调用格式为：scatterplot3d（x，y，z，…）。其中，x，y，z都是数值向量，且x被绘制在水平轴上，y被绘制在竖直轴上，z被绘制在水透视上．

＞install．packages(＂scatterplot3d＂)

＞library(scatterplot3d)

＞scatterplot3d(iris[2：4])

结果如图2-14所示．

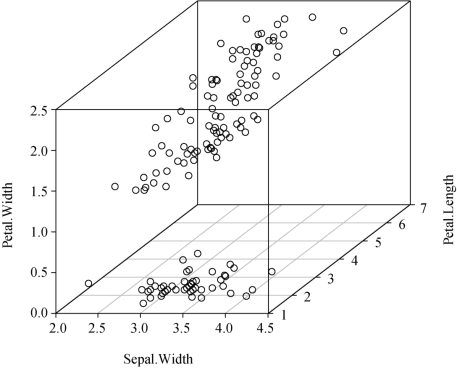
pagenumber_ebook=35,pagenumber_book=26