在实验2．3．1中，我们对mtcars数据集进行了展示和描述．在实验2．3．3中，我们对mtcars数据集进行了可视化．现在我们对该数据集中的变量进行回归分析．（1）不考虑变量交互项对该数据集，如果把mpg（汽车每加仑公里数）作为因变量，自变量为hp（马力）和wt（汽车重量）进行回归．＞fit＜－lm(mpg～hp＋wt,data＝mtcars)＞summary(fit)结果如下：得到的回归方程为......
2023-11-18
基于R的多元统计分析：mtcars数据集可视化
【摘要】：在实验2．3．1中，我们对mtcars数据集（R 自带数据集）进行了展示和描述，以下对该数据集进行可视化．（1）汽车每加仑英里数直方图＞hist(mtcars＄mpg,breaks＝10)结果如图2-1所示．（2）按汽缸数划分的各车型车重的核密度图＞par(lwd＝2)＞library(sm)＞cyl．f＜－factor(mtcars＄cyl,levels＝c(4,6,8),labels＝c(＂4
在实验2．3．1中，我们对mtcars数据集（R 自带数据集）进行了展示和描述，以下对该数据集进行可视化．
＞hist(mtcars＄mpg,breaks＝10)
结果如图2-1所示．
（2）按汽缸数划分的各车型车重的核密度图
＞par(lwd＝2)
＞library(sm)
＞cyl．f＜－factor(mtcars＄cyl,levels＝c(4,6,8),labels＝c(＂4cylinder＂,＂6cylinder＂,＂8cylinder＂))
＞sm．density．compare(mtcars＄wt,mtcars＄cyl,xlab＝＂CarWeight＂)
＞title(main＝＂CarWeightbyCarCylinders＂)
＞colfill＜－c(2：(１＋length(levels(cyl．f))))
＞legend(locator(1),levels(cyl．f),fill＝colfill)
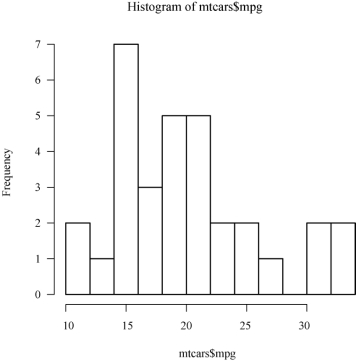
图2-1 汽车每加仑英里数直方图
结果如图2-2所示．
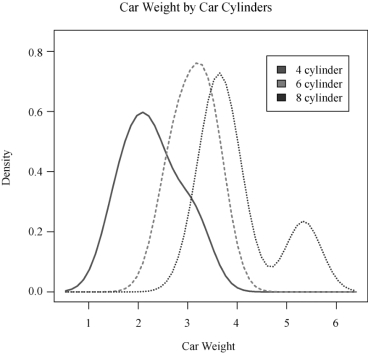
图2-2 按汽缸数划分的各车型车重的核密度图
＞x＜－mt cars[order(mt cars＄mpg),]
＞x＄cyl＜－factor(x＄cyl)
＞x＄color[x＄cyl＝＝4]＜－＂red＂(www.chuimin.cn)
＞x＄color[x＄cyl＝＝6]＜－＂blue＂
＞x＄color[x＄cyl＝＝8]＜－＂green＂
＞dot char t(x＄mpg,labels＝row．names(x),cex＝．7,groups＝x＄cyl,gcolor＝＂black＂,color＝x＄color,pch＝19,main＝＂Gas Mileage for Car Models\ngrouped by cylinder＂,xlab＝＂Miles Per Gallon＂)
结果如图2-3所示．
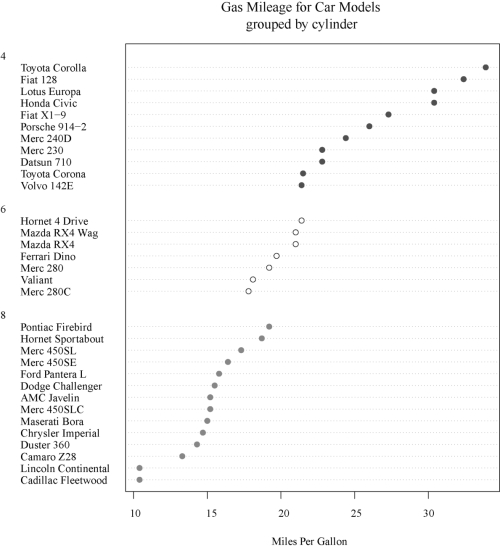
图2-3 依气缸数量分组的每加仑汽油行驶英里数点图
（4）各汽车马力与每加仑汽油行驶英里数的散点图
plot(mt cars＄mpg,mt cars＄hp,main＝＂The Histogram of\n Gross horsepower and MilesPer Gallon＂)
结果如图2-4所示．
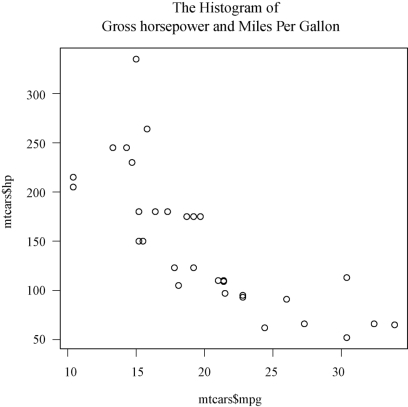
图2-4 各汽车马力与每加仑汽油行驶英里数的散点图
（5）不同变速箱类型和气缸数量车型的箱线图
＞mtcars＄cyl．c＜－factor(mtcars＄cyl,levels＝c(4,6,8),labels＝c(＂4＂,＂6＂,＂8＂))
＞mtcars＄am．c＜－factor(mtcars＄am,levels＝c(0,1),labels＝c(＂auto＂,＂stand-ard＂))
＞boxplot(mpg～am．c∗cyl．c,data＝mtcars,varwidth＝TRUE,col＝c(＂gold＂,＂dark-green＂),
main＝＂MPG Distribution by Auto Type＂,xlab＝＂Auto Type＂)
结果如图2-5所示．
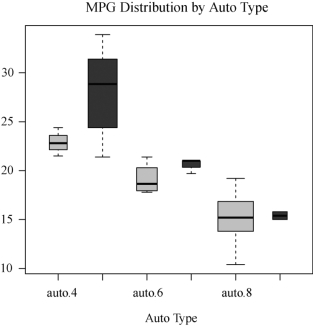
图2-5 不同变速箱类型和气缸数量车型的箱线图
有关应用多元统计分析：基于R的实验的文章
- 详细阅读
-
利用R进行多元统计分析实验，可视化iris数详细阅读
在实验2．3．2中对iris数据集进行了描述和展示，以下对iris数据集进行可视化．花萼长度、花萼宽度、花瓣长度、花瓣宽度的小提琴图小提琴图是箱线图的变种，因为形状酷似小提琴而得名．小提琴图是将箱线图与核密度图结合在一起，它在箱线图上以镜像方式叠加上核密度图．绘制小提琴图，可以使用vioplot包中的“vioplot（ ）”函数，但在第一次使用之前请先安装vioplot包．“vioplot（ ）”函数的调用格式为：vioplot（x1，x2，…......
2023-11-18
-
UScereal数据集方差分析：基于R的多元详细阅读
用MASS包中的UScereal数据集，我们研究美国谷物中的卡路里、脂肪和糖含量是否会因为储存架位置的不同而发生变化．其中1代表底层货架，2代表中层货架，3代表顶层货架．卡路里（calories）、脂肪（fat）和糖（sugars）含量是因变量，货架是3水平（1，2，3）的自变量．（1）单因素多元方差分析在以上代码中，“cbind（ ）”函数将三个变量（calories，fat，sugars）合并......
2023-11-18
-
基于R的多元统计分析：Bayes判别详细阅读
根据上面的叙述，要选择样本空间Ω 的一个划分R1 和R2＝Ω－R1，使得平均误判损失ECM 达到极小．定理8．3．1 极小化平均误判损失式的区域R1 和R2 为说明：当时，即x 为边界点，它可以归入R1 和R2中的任何一个，为了方便就将它归入R1．根据定理8．3．1，得到两总体的Bayes判别准则：应用此准则时仅需要计算：新样本点x0＝（x01，x02，…......
2023-11-18
-
基于R的应用多元统计分析成果详细阅读
，F5 的线性组合表示出来Xi＝μi＋ai1 F1＋ai2 F2＋…，F5 的值却是未知的，有关参数的意义也有很大的差异．因子分析的首要任务就是估计因子载荷aij 和方差σ2i，然后给因子Fi 一个合理的解释，若难以进行合理的解释，则需要进一步作因子旋转，希望旋转后能发现比较合理的解释．特别需要说明的是这里的因子和试验设计里的因子（或因素）是不同的，它比较抽象和概括，往往是不可以单独测量的．......
2023-11-18
-
使用多元统计分析随R展示和描述iris数据集详细阅读
iris数据集是R 自带的数据集，以下对该数据集进行描述和展示．（1）展示iris数据集的前几行＞head(iris)结果如下：其中Sepal．Length，Sepal．Width，Petal．Length，Petal．Width，Species，分别表示（鸢尾花）花萼（Sepal）的长度，花萼的宽度，花瓣（Petal）的长度，花瓣的宽度以及每个观测值来自哪一种类．（2）对鸢尾花数据集的数据进行描......
2023-11-18
-
应用多元统计分析：数据可视化与表示详细阅读
，xn 是从一元总体中抽取的．一元数据的数字特征主要有：均值，方差s2＝，标准差s＝，等等．对于多元数据，除分析各分量的取值特征外，还要分析各分量之间的相关关系．由于多元统计分析中的符号多而杂，因此需要说明：在一元统计学中一般用大写和小写字母分别来区分随机变量及其观测值，在本书后面的章节里，由于其他复杂的符号，我们可能不再遵守此约定，请读者注意一个符号在每一章中的意义．......
2023-11-18
-
应用多元统计分析方法：基于R实验详细阅读
多元统计分析是统计学中应用性很强的一个分支，它的应用范围十分广泛．多元统计分析可以应用于几乎所有的领域，主要包括经济学、农业、地质学、医学、工业、气象学、金融、精算、物理学、地理学、军事科学、文学、法律、环境科学、考古学、体育科学、遗传学、教育学、生物学、管理科学、水文学等，还有一些交叉学科或方向等．多元统计分析的应用实在是难以一一罗列，以下简要地介绍一下多元统计分析在文学、数据挖掘（作为交叉学科......
2023-11-18
相关推荐