STEM+A与艺术：整合资源下的教育未来

2023-11-18 理论教育版权反馈

【摘要】：在视觉艺术的发展过程中，数学始终是艺术家创作的辅助工具。此后，艺术家们也一直沿用其中的1∶的法则为理想的男性裸体画规范比例。在古典希腊、罗马和文艺复兴时期的雕塑中，这项人体“规则”的影响是巨大的，尽管波利克利托斯的原作并没有幸存下来，但罗马时期的复制品仍可展现出他将数学精确的计算与人体完美结合的理想。

数学（Mathematics）一词来自于希腊文，有“知识、研究、学习”的含义，包括数量、结构、空间和变化等系统内容，被称为“开启大自然的钥匙”。而从神话的历史看，有法力的语言要重复到一定的次数，所以人们对数字以及对数字的顺序始终怀有一种神秘感，但也由此证明，数字（数学）的出现是人们相信它像语言一样是构成宇宙的最基本的东西。长期以来人们一直将艺术和数学作为两种截然不同的学科加以区分并认为二者并无结合之处，但数学和艺术却有着深层关联，而且数学本身也被描述为一门由美驱动的艺术，数学中的对称、随机、透视法、符号化、迭代法、模型、无穷大、无穷小、空间、平衡、无秩序、等值等概念在绘画、音乐、舞蹈、建筑、雕塑等艺术形式中都能找到其存在的依据（见图2.2.3）。

在视觉艺术的发展过程中，数学始终是艺术家创作的辅助工具。比如绘画中的“透视”（Perspective），该词在拉丁语中的涵义为“看穿”，即指在一个平面上用眼睛看到的图像。意大利文艺复兴时期建筑的创始人菲利普·布鲁内尔斯基（Filippo Brunelleschi，1377—1446)担任设计的佛罗伦萨大教堂的穹顶，便被视为建筑设计中的壮举，也是艺术中线性透视和数学空间完美结合的体现。1418年，当教堂的主体建筑基本完工时，它的顶部并没有被设计出来，甚至没有人想到会建造如此巨大的圆顶。但布鲁内尔斯基却使用400多万块砖建造了教堂的八角形穹顶，顶高107米，跨度42.2米，成为欧洲当时最大的穹顶。布鲁内尔斯基的成功很大程度上归功于他在数学方面的天才，为了减弱穹顶对支撑的鼓座的侧推力，他在结构上大胆采用了双层骨架券，而八角形的棱角处通过承重构件结构，与顶上的采光亭连接成为整体，从而使其能够支撑起全部重量。同时，令人吃惊之处还在于这个穹顶的设计并没有留下详细的建筑平面图，但却通过精确的计算使这座建筑历经百年屹立不倒。由此，布鲁内尔斯基的这项设计成就，被公认为是意大利文艺复兴时期的重要杰作之一，指导了其后绘画的发展，甚至影响了19世纪末现代科学的兴起。

pagenumber_ebook=75,pagenumber_book=66

图2.2.3阿尔布雷特·杜雷尔的铜版雕刻《梅伦科里亚一世》，1514年。数学参考包括一个几何罗盘、一个魔方和一个截头菱形体，而测量由刻度和沙漏表示

公元前4世纪古希腊雕塑家波利克利托斯（Polykleitos，生卒年代不详，与雅典雕塑家菲迪亚斯Pheidias、迈伦Myron和普莱西特尔斯Praxiteles，被认为是古典艺术中最重要的雕塑家之一）创造了一种雕塑方法，同时还撰写了一篇论述人体比例的论文“Kanon”（规则），以此来证明他关于人体比例在数学基础上的美学理论。此后，艺术家们也一直沿用其中的1∶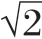 pagenumber_ebook=75,pagenumber_book=66 的法则为理想的男性裸体画规范比例。即将远端指骨的长度乘以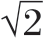的平方根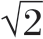（）得到第二个指骨的距离，并将长度再乘以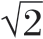，得到第三个指骨的长度。接下来，将手指长度乘以，得到从手指底部到尺骨的手掌长度。这一几何系列的测量方式一直进行应用到形成手臂、胸部、身体等等。在古典希腊、罗马和文艺复兴时期的雕塑中，这项人体“规则”的影响是巨大的，尽管波利克利托斯的原作并没有幸存下来，但罗马时期的复制品仍可展现出他将数学精确的计算与人体完美结合的理想。一些学者认为波利克利托斯在一定程度上受到了古希腊数学家和哲学家毕达哥拉斯（Pythagoras，B.C.570—B.C.490年，古希腊爱奥尼亚哲学家，也是毕达哥拉斯主义的同名创始人）的影响，即“Kanon”基于古希腊的数学概念，如比率、比例和对称性等内容，通过一系列计算将其转化为可以描述人类形态的系统。

此外，在艺术中最为著名的一个经典概念就是“黄金分割”（Golden Section），即当事物的整体被分为不均等的两部分时，如果两个量的比值等于它们的总和与两个量中较大者的比值，那么这两个量属于黄金分割，即1∶0.618；而其中具有这一比值的点，被称作黄金分割点。在人体形态中，存在很多具有黄金分割的比例关系，如以人体分为上下两部分时，人体的身长与肚脐以下部分的比例关系恰好接近1∶0.618，肚脐即处于黄金分割点部位。咽喉为人体头顶到肚脐的黄金分割点，左右膝关节是人体肚脐到左右足底距离的黄金分割点，而人类的面部与五官所构成的矩形，其长宽比例也为1∶0.618形式的“黄金分割矩形”。包括欧几里德（Euclid，公元四世纪中叶—公元三世纪中叶，希腊数学家，几何学之父，他的《元素》Elements被认为是世界数学史上最有影响力的作品之一，自出版之日直至19世纪末20世纪初，一直成为教授数学，尤其是几何的主要教科书）在内的很多数学家在研究“黄金分割”比例之后，发现黄金矩形还可以被切割成具有相同长宽比例的正方形或较小的矩形。可见，这些自然世界中的神奇现象不仅真实的存在于我们身边，更因其令人感到愉悦的美感，成为除数学家之外的艺术家、音乐家、历史学家、建筑师、生物学家和心理学家都为之着迷的课题。从某种意义上说，“黄金分割”激励了历史上所有学科的思想家，也完美地融合了艺术与数学的差别，诞生了众多集严谨、精确、和谐、优美为一体的经典之作。如列奥纳多·达·芬奇（Leonardo di ser Piero da Vinci，1452—1519）的《蒙娜丽莎》（图2.2.4）、萨尔瓦多·达利（Salvador Dalí，1904—1989）的《最后晚餐的圣礼》（图2.2.5）、帕特农神庙（Parthenon，B.C.447—B.C.432）、沙特尔大教堂（Chartres Cathedral，1194—1220，被称为“法国哥特式艺术的巅峰”）、劳恩圣母院（Laon Cathedral，1157—1205，位于法国劳恩，早期哥特式风格建筑最重要的范例之一，1840年以来一直被公认为历史遗迹）和巴黎圣母院（Notre-Dame de Paris，1160—1260，法国哥特式建筑的最佳范例之一）的建筑设计、斯特拉迪瓦里（Antonio Stradivari，1644—1737）制作的小提琴、苹果iPod播放机等。

pagenumber_ebook=78,pagenumber_book=69

图2.2.4黄金矩形在《蒙娜丽莎》作品中的使用

pagenumber_ebook=78,pagenumber_book=69 (www.chuimin.cn)

图2.2.5萨尔瓦多·达利（Salvador Dalí，1904—1989）《最后晚餐的圣礼》（The Sacrament of the Last Supper）,画面中的人物和画外的观众都处于五边形组成的十二面体中，而在柏拉图认为，十二面体并不仅仅是原子的形状，而是整个宇宙的形状

正如数学家杰瑞·金（Jerry P.King）所说，数学的关键是美和优雅，而不是枯燥和技术性，因此美是数学研究的动力。同时他将严肃性、普遍性、必然性和具有深度的数学标准称之为“审美愉悦”。事实上，从古希腊直至20世纪之后的艺术发展，都离不开数学作为基础要素的作用，如分形几何（Fractal geometry）在艺术创作中的使用。众所周知，分形是用来描述和模拟自然中的物体的某种重复特性，这种重复性一旦形成某种规律，即可使事物具有一定的美感，而分形也被称为数学与艺术最完美的结合。当利用一定的分形原理来审视某些艺术作品时，我们会发现很多绘画里的艺术形式都具有这种数学元素，如日本浮世绘艺术家葛饰北斋（Katsushika Hokusai，1760—1849）创作的《富嶽三十六景》《凯风快晴》《神奈川县的大浪》等作品，其中对云浪、海浪、冰川等形态的描绘就大量使用了分形几何的表现形式，使其作品中充满了具有现代感的艺术风格并直接影响了19世纪欧洲艺术家的创作，像印象主义的克劳德·莫奈、雷诺阿、高更、梵·高的作品中，都能看到葛饰北斋创造的“超越时代和国界”的艺术语言（见图2.2.6）。

pagenumber_ebook=79,pagenumber_book=70

图2.2.6葛饰北斋《富嶽三十六景》

此外，法国数学家亨利·庞加莱（Jules Henri Poincaré，1854—1912）也曾提出四维空间的存在激发了艺术家们对古典文艺复兴时期观察视角的质疑，为此绘画可以通过数学的方式，在颜色和形式上进行表达，进而促成了立体主义和抽象艺术的发展。

进入21世纪之后，数字媒体艺术（Digital media art）的发展在更广泛的层面上对艺术创作起到了推动作用，成为艺术和数字化形式结合的产物。因为数字媒体与艺术的相加，体现为更注重思维的“非线性”（Non-linear），媒介的交互性（Interactivity）、可扩展性和延伸性。所谓“非线性”即相对于“线性”的一种沟通变量之间的形式。数字媒体艺术出现后，非线性的叙事方式和思维方式便成为一种具有开放和多重性质的实践方法。它结合网络的超文本链接模式，在一个新的意识水平上把各类直觉、想象、知识和经验整合起来，从而强调了各种可能出现的意义，即世界是由无数“可能性”所组成的，任何事件的发生和结果只是它众多可能性中的之一；而另一方面，这种开放的因果关系，也仍然存在着多样性、互动性和转化性。“交互性”是一个带有有限数据集的封闭系统，这个有意义的形式拥有开放式的能力，以适应各种新的变数。

如果说20世纪的艺术的使命是使各种无形变为可视化，那么21世纪的艺术是利用各种兼容的信息载体创造新的艺术环境和媒体文化，它不再是既成的、有限的和单一的，而是具有帮助性和引导性的。这种变化既预示着艺术家的角色从过去的创造者转变为参与者和资源共享者，也体现在他们需要帮助人类发现有形物体中的无形信息，从而参与到艺术的更新和重建中。

STEM+A与艺术：整合资源下的教育未来

相关推荐