首页 理论教育儿童魔方之旅-解谜-儿童魔方之旅

儿童魔方之旅-解谜-儿童魔方之旅

2023-11-18 理论教育 版权反馈
【摘要】：在还原了第三层4个棱块的方向之后，这一章我们要学习还原第三层4个角块的方向。目的是让第三层4个角块的白色贴纸全部朝上，图7.1是完成后的状况，此时全部9张白色贴纸都已经朝上了。由于每个角块有3种不同的方向，因此这一步可能出现的状态与棱块方向相比要复杂一些。

在还原了第三层4个棱块的方向之后，这一章我们要学习还原第三层4个角块的方向。目的是让第三层4个角块的白色贴纸全部朝上，图7.1是完成后的状况，此时全部9张白色贴纸都已经朝上了。

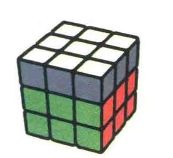
图7.1

首先还是观察一下魔方U层4个角块白色贴纸的朝向，它们可能朝上，也可能朝向前后左右各个侧面。由于每个角块有3种不同的方向，因此这一步可能出现的状态与棱块方向相比要复杂一些。归纳起来，这时角块方向的组合一共有以下8种状态（图7.2-图7.17）：

状态1

图7.2

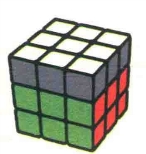
图7.3

状态2

图7.4

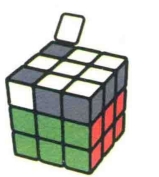
图7.5

状态3

图7.6

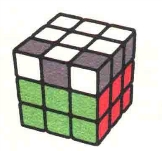
图7.7

状态4

图7.8

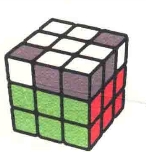
图7.9

状态5

图7.10

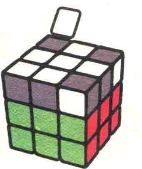
图7.11

状态6

图7.12

图7.13

状态7

图7.14

图7.15

状态8

图7.16

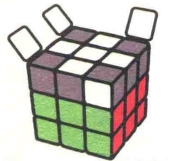
图7.17

状态1是4个角块白色贴纸全部朝上的情况。同上一章一样，如果你恰巧遇到了这种状态，就意味着你跳过了这一还原角块方向的步骤，这样的情况你平均还原27次魔方会遇到一次。

有两个角块白色贴纸朝上的状态共有3种。

只有一个角块白色贴纸朝上的状态共有两种。

还有两种状态没有一个角块白色贴纸朝上。

也许又有小朋友会问，为什么没有给出3个角块白色贴纸朝上，另一个角块白色贴纸朝向侧面的状态呢（图7.18-图7.19）？

和上一章的棱块方向一个道理，如果你遇到了这种状态，先检查一下第一层的4个角块是否确实已经还原，如果还原无误的话，就说明你的魔方装错了，因为在其他7个角块方向不变的前提下单独扭转一个角块是不可能的，这种状态无论如何都无法还原。不仅如此，如果你遇到的是其他不同于以上8种的状态，也都是因为你的魔方装错了。

万一你遇到了装错的情况，你可以先将一个U层棱块拆下来，再扭转和这个棱块相邻的一个角块的方向，使U层4个角块的方向符合上面8种状态中的任意一种，最后再将这个棱块装回去。

当然，有的魔方也可以直接扭转角块的方向，我们建议你先轻轻试一试能否直接扭动一个角块，如果它很难扭动，就不要再尝试这种方式，因为粗暴地扭动角块很可能会损坏你的魔方。

图7.18

图7.19

状态1之外的7种状态就是这一章中需要处理的。同上一章类似，在这里我们仍然给出逐个还原法和直接还原法两种方法。

这一次我们先说直接还原法。我们详细给出了7种状态各自所使用的公式。同上一章一样，当你遇到图中任意一种状态时都可以运用我们给出的对应公式进行还原（要注意，在魔方U层的朝向和图中一致时再做公式）。

公式7-1：rUR'U'L'URU'x'

状态2

图7.20

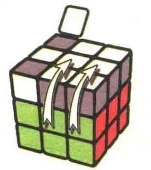
图7.21：r

图7.22：U

图7.23：R'

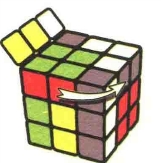
图7.24：U'

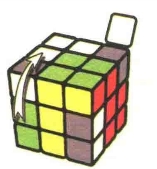
图7.25：L'

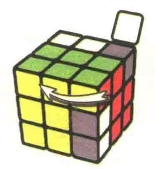
图7.26：U

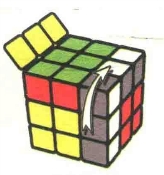
图7.27：R

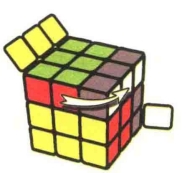
图7.28：U'

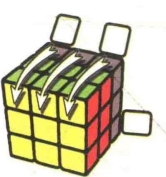
图7.29：x'

图7.30

公式7-2：xUR'U'LURU'r'

状态3

图7.31

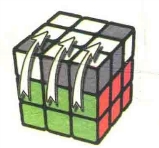
图7.32：x

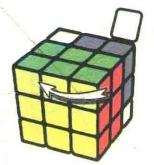
图7.33：U

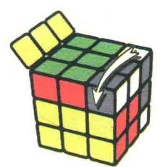
图7.34：R'

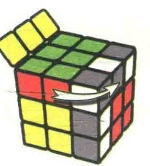
图7.35：U'

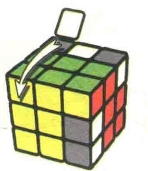
图7.36：L

图7.37：U

图7.38：R

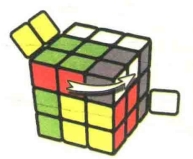
图7.39：U'

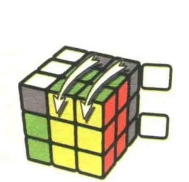
图7.40：r'

图7.41

公式7-3：R2DR'U2RD'R'U2R'

状态4

图7.42

图7.43：R2

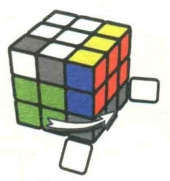
图7.44：D

图7.45：R'

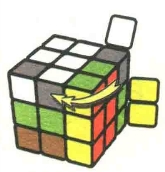
图7.46：U2

图7.47：R

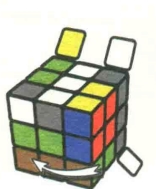
图7.48：D'

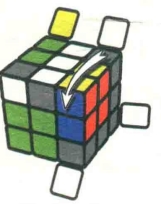
图7.49：R'

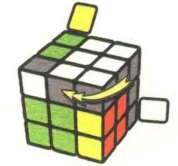
图7.50：U2

图7.51：R'

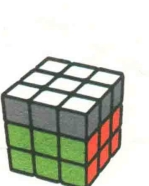
图7.52

公式7-4：RUR'URU2R'

状态5

图7.53

(www.chuimin.cn)

图7.54：R

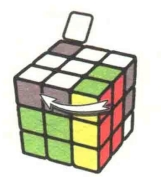
图7.55：U

图7.56：R'

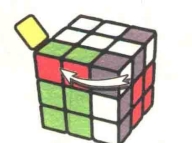
图7.57：U

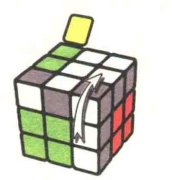
图7.58：R

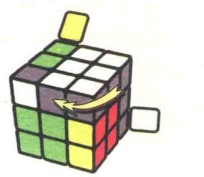
图7.59：U2

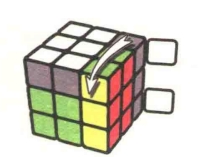
图7.60：R'

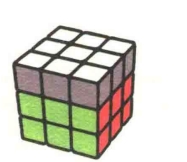
图7.61

公式7-5：R'U'RU'R'U2R

状态6

图7.62

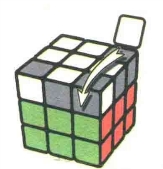
图7.63：R'

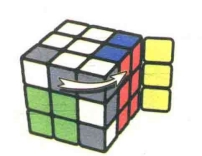
图7.64：U'

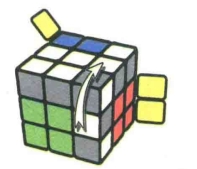
图7.65：R

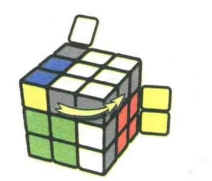
图7.68：U2

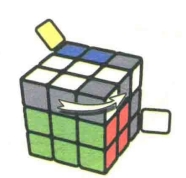
图7.66：U'

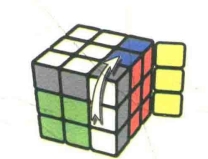
图7.69：R

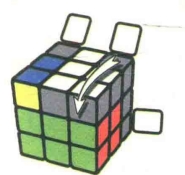
图7.67：R'

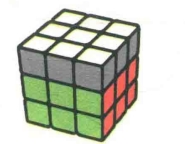
图7.70

公式7-6：RUR'URU'R'URU2R'

状态7

图7.71

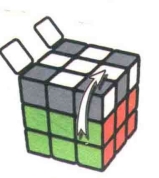
图7.72：R

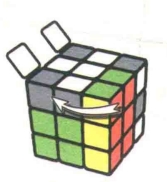
图7.73：U

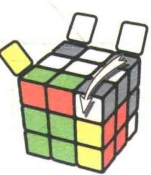
图7.74：R'

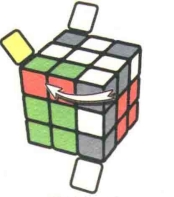
图7.75：U

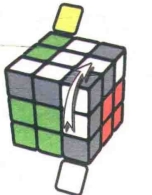
图7.76：R

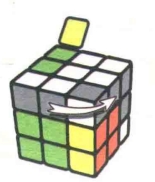
图7.77：U'

图7.78：R'

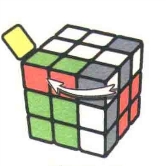
图7.79：U

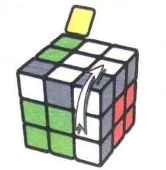
图7.80：R

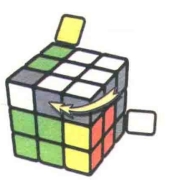
图7.81：U2

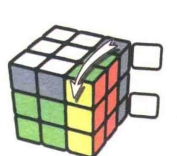
图7.82：R'

图7.83

公式7-7：RU2R2U'R2U'R2U2R

状态8

图7.84

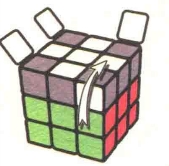
图7.85：R

图7.86：U2

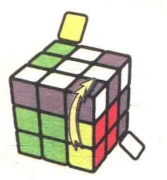
图7.87：R2

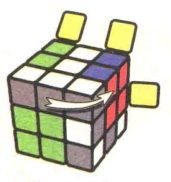
图7.88：U'

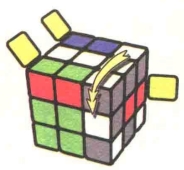
图7.89：R2

图7.90：U'

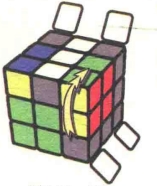
图7.91：R2

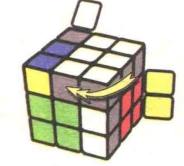
图7.92：U2

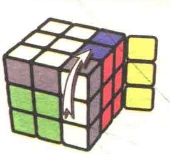
图7.93：R

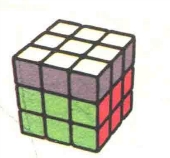
图7.94

但作为初学者，不大可能有人愿意一下子记忆这么多的公式，死记硬背公式也有违我们这本书的初衷，那怎么办呢？幸好，这7个公式仍然有规律可循。

通过观察我们会发现，公式7-1和公式7-2互为“逆公式”，也就是说，公式7-2实际上就是把公式7-1倒过来做一遍。

与前面出现过的左右镜像类似，状态5和状态6是“前后镜像”的，公式7-4和公式7-5互为“前后镜像公式”。

状态7很有意思，拿起你的魔方做一下公式7-6，是不是感觉和7-4有点像？是的，实际上公式7-6是连续做了两遍公式7-4：

（RUR'URU2R'）2

=RUR'URU2R'+RUR'URU2R'

=RUR'UR+（U2R'+RU）+R'URU2R'

=RUR'UR+U'+R'URU2R'

可以看到，当我们连续做两遍公式7-4时，前一个公式最后的U2R'与后一个公式最开始的RU相互抵消，结果只相当于做了一步U'。

在上一章中，使用直接还原法时，由于棱块方向只需要处理3种状态，公式又很好学，小朋友们可能会觉得逐个还原法的用处不大。但现在角块方向需要处理的状态多达7种，虽然我们发现了它们的一些相互关系，有助于你记忆它们，但是，一次记住7个公式仍是很麻烦的事情。而且对不追求速度的小朋友来说，更没有必要记这么多的公式。因此，逐个还原法的优势在这里就显现出来了。

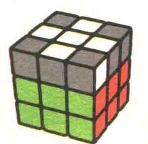
图7.95

我们先转动U层，将一个需要扭转方向的角块移动到UFR位置上，显然你会遇到下面两种状态中的一种（图7.95-图7.96）。

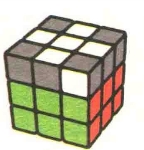
图7.96

然后使用公式7-8：

公式7-8：（R'D'RD）2

图7.97

图7.98

由于对一个魔方来说，在其他7个角块方向不变的前提下单独扭转一个角块是不可能的，所以同上一章的公式6-1一样，这个公式也是通过改变前两层已经还原的部分的状态来实现对UFR角块的扭转。仍以一个完全还原的魔方为例，如图所示，做完这个公式后，前两层有3个角块和3个棱块的状态发生了变化，同时UFR角块完成了一次逆时针扭转，而魔方其他块的状态都保持原样（图7.97-图7.98）。

这个公式影响的块比较多，但不用担心，当我们连续做3次这个公式的时候，这6个块就又恢复到了还原的状态（图7.99-图7.102）。

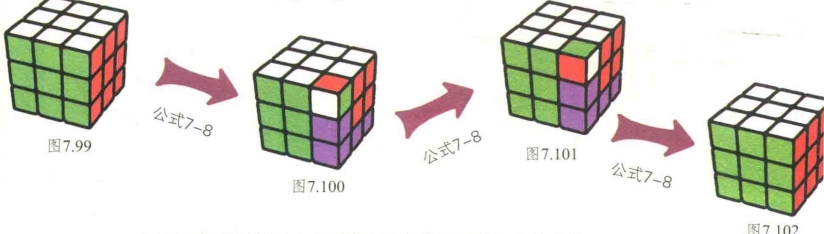
于是我们可以使用它来不断扭转处在UFR位置上的角块。

如果这个角块的初始状态如图7.95所示，那么在做了一次公式7-8之后，它的白色贴纸就被扭转为朝上，接下来我们可以转动U层，将另一个需要扭转的角块转到UFR位置，重复这一步骤。如果这个角块的初始状态如图7.96所示，则需要连续做两次公式7-8。

这个公式和前面的7-3都出现了D层转，我们可以用左右手的无名指拨动D层。

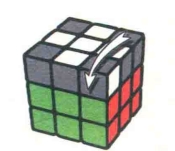
图7.103：R '

图7.104：D'

图7.105：R

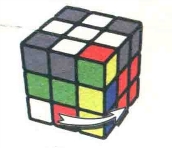
图7.106：D

图7.107：R'

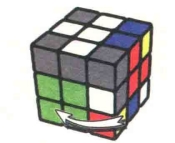
图7.108：D'

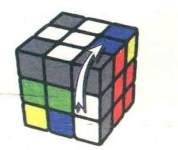
图7.109：R

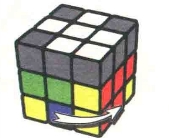
图7.110：D

图7.111

需要注意D和D'分别的转动方向，不要搞错。以图7.95的状态为例（图7.103-图7.111），仔细看一下公式7-8的转动过程，你会发现这个公式其实和我们最熟悉的公式2-1是有联系的。我们在前面已经接触到了左右镜像公式和前后镜像公式，除了这两种之外还有一种“上下镜像公式”，也就是说，一个公式的每一步都和另一个公式是上下对称的，就像我们坐在湖边看岸上的树木在水中的倒影一样。公式7-8中重复的4步和公式2-1就属于上下镜像公式，小朋友们可以自己对照前面公式2-1的示意图看一看。

这样，我们通过不断转动U层和使用公式7-8，就可以解决以上7种状态中的任意一种。总共使用公式7-8的次数或者是3次，或者是6次。无论哪种情况，当第三层4个角块的方向都已经还原时，前两层的6个块也刚好恢复到还原的状态。

有关儿童魔方之旅的文章

  • 儿童魔方之旅：准备标准配色魔方 儿童魔方之旅：准备标准配色魔方

    在阅读后面的章节之前，你需要先准备一个标准配色的魔方。图1.3：一个“盖子”完全掀开的魔方不同厂家生产的魔方贴纸颜色略有区别，尤其是褐色的这一面，有的更接近橙色，有的更接近粉色。正常情况下，我们一次只能看到魔方的3个面，在图1.2中，我们用了类似“掀盖子”的方法来表现我们看不到的那3个面的颜色。全部“盖子”都掀起来之后的样子如图1.3。......

    2023-11-18

    详细阅读
  • 儿童魔方之旅：角块位置 儿童魔方之旅：角块位置

    图8.18另一种方法是使用公式8-2，它一共有14步：公式8-2：2这个公式是一个7步的公式重复做两次，对比一下就会发现它和公式8-1是有联系的，它的前6步和公式8-1完全一样，我们仍然用示意图来表示：掌握了这两个公式，我们就可以完成第三层角块位置的还原了。......

    2023-11-18

    详细阅读
  • 儿童魔方之旅：左撇子小朋友的方便公式 儿童魔方之旅：左撇子小朋友的方便公式

    但是，阅读这本书的小朋友中一定会有少部分是左撇子，对这部分小朋友来说，有些公式就不那么顺手了。别急，本书的作者和你们一样也是左撇子，下面我们就来讲解一下如何用方便左手完成的公式来还原魔方。第四章中的公式4-1和4-3就是如此。左撇子小朋友可以自己尝试一下。......

    2023-11-18

    详细阅读
  • 第三层棱块方向-儿童魔方之旅 第三层棱块方向-儿童魔方之旅

    由于在这个步骤中，需要翻转的第三层棱块数量一定是偶数，我们的目的便是利用UR这个位置，将需要翻转的第三层棱块依次移动到那里，用公式6-1逐个翻转这些棱块的方向，同时反复翻转3个位于M层的棱块，最后当全部第三层棱块方向都正确的时候，这3个M层棱块恰好也翻转回了原来的方向。......

    2023-11-18

    详细阅读
  • 儿童魔方之旅：第三层棱块定位 儿童魔方之旅：第三层棱块定位

    在还原了第三层角块位置之后，这一章我们终于来到了最后一步：还原第三层棱块位置。图9.4图9.5图9.6图9.7这种情况的实质，是这3个棱块依次移动了位置。如果你遇到的是前一种状态，先让已经还原的那个面背对着自己，再做公式9-1：公式9-1：RU'RURURU'R'U'R2这个公式共有11步，比较复杂，你仍然可以通过观察黄色贴纸的移动轨迹来记忆它：很显然，由于它的作用是让3个棱块依次移动位置，如果你连续做3次这个公式，魔方就回到了一开始的状态。......

    2023-11-18

    详细阅读
  • 儿童魔方之旅：第二层棱块还原教程 儿童魔方之旅：第二层棱块还原教程

    图5.1图5.2在这一章里，我们要学习还原魔方的第二层棱块。而中心块相互之间的位置又是不会变的，因此还原了第二层的4个棱块也就等于还原了第二层，即图5.1中用紫色表示的部分。）我们假设你找到的是绿红棱块，将这个棱块移动到UF位置。对于图5.6的状态，则需要将绿红棱块还原到FL位置，同样是绿色贴纸挨着绿色中心块，红色贴纸挨着红色中心块。不断重复直到第二层的4个棱块全部还原，此时整个第二层也还原了。......

    2023-11-18

    详细阅读
  • 儿童魔方之旅：还原第一层角块的技巧 儿童魔方之旅：还原第一层角块的技巧

    如果你已经能熟练还原第一层的4个棱块，我们就可以接着学习还原第一层的4个角块。同第一层的4个棱块一样，这4个角块的共同特点也是都拥有一张黄色贴纸。在第一种状态中，我们要把黄色贴纸朝右的UFR角块还原到DFR位置，而现在这种状态则要把黄色贴纸朝左的UFL角块还原到DFL位置。......

    2023-11-18

    详细阅读
  • 儿童魔方之旅：第一层棱块正确还原的方法 儿童魔方之旅：第一层棱块正确还原的方法

    但当我们还原好第一个棱块，接下来还原第二个棱块时，就要防止在还原第二个棱块的过程中，将已经还原好的第一个棱块破坏掉。根据其黄色贴纸的朝向，转动U层，使得UF或UR位置上出现一个空位，转动F层或R层，将这个棱块移动到U层。通过这一章的学习，小朋友们不仅能学会第一层棱块的还原方法，在反复练习的过程中，也能更加明了魔方的结构和转动方式，这对后面章节的学习很有好处。......

    2023-11-18

    详细阅读