计算机中的数制及转换

2025-09-30 理论教育版权反馈

【摘要】：1．进位计数制进位计数制即按进位原则进行计数的方法。每个数字所表示的值是该数字与它相应的权Ri的乘积。表1－2各种进位制的对应关系2．不同进制数的相互转换二、八、十六进制转换成十进制把二、八、十六进制数按权展开即得到其十进制数。将10转换成二、八、十六进制数。

1．进位计数制

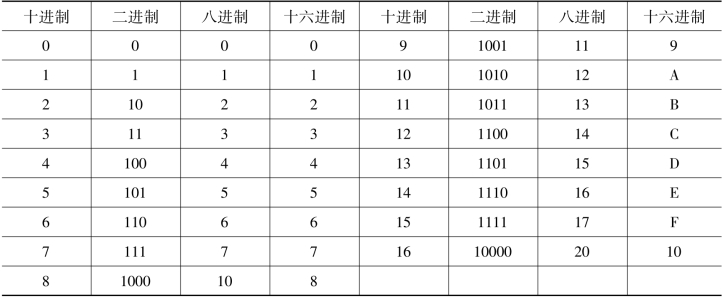
进位计数制即按进位原则进行计数的方法。十进制数的特点如下：有10个不同的数字符号0，1，2，…，9；低位向高位进位的规律是“逢十进一”；同一个数字符号在不同的位时所表示的数值是不同的。从表1－2可以看出各种进位制的对应关系。

对R进制的数N，计数原则是“逢R进一”，可以按权展开为

式中，ai是0，1，…，（R－1）中的任一个数，m、n是正整数，R是基数。每个数字所表示的值是该数字与它相应的权Ri的乘积。

（1）二进制数

二进制数中，只有0和1两个数码，进位规律为“逢二进一”，表示为10110010B。

（2）八进制数

八进制数中，有0，1，2，…，7共8个数码，进位规律为“逢八进一”。

（3）十六进制

十六进制中，有0，1，2，…，9，A，B，C，D，E，F共16个数码，进位方法是“逢十六进一”，表示为8FH。

表1－2　各种进位制的对应关系

pagenumber_ebook=18,pagenumber_book=11

2．不同进制数的相互转换

（1）二、八、十六进制转换成十进制

把二、八、十六进制数按权展开即得到其十进制数。

【例1－1】将数（101．01）2、（537．12）8、（5D．A4）16转换为十进制。(https://www.chuimin.cn)

【解】（101．01）2=1×22+0×21+1×20+0×2－1+1×2－2=5．25

（537．12）8=5×82+3×81+7×80+1×8－1+2×8－2=351．15625

（5D．A4）16=5×161+13×160+10×16－1+4×16－2=93．640625

（2）十进制转换成二、八、十六进制

任意十进制数N转换成R进制数，需将整数部分和小数部分分开，采用不同方法分别进行转换，然后用小数点将这两部分连接起来。

1）整数部分：除基取余法。分别用基数R不断地去除N的整数，直到商为零为止，每次所得的余数按照最初得到的为最低有效数字、最后得到的为最高有效数字排列的数字即为相应进制的数码。

【例1－2】将（168）10转换成二、八、十六进制数。

【解】

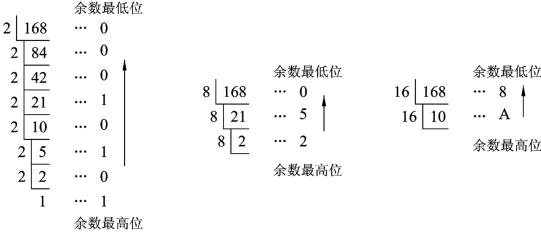
pagenumber_ebook=19,pagenumber_book=12

故（168）10=（10101000）2=（250）8=（A8）16。

2）小数部分：乘基取整法。分别用基数R不断地去乘N的小数，直到积的小数部分为零（或直到所要求的位数）为止，每次乘得的整数按照最初得到的为最高有效数字，最后得到的为最低有效数字排列即为相应进制的数码。

【例1－3】将（0．645）10转换成二、八、十六进制数。

【解】

pagenumber_ebook=19,pagenumber_book=12

故（0．645）10=（0．10100）2=（0．51217）8=（0．A51EB）16。