国内生态模型研究案例实例

一、森林-草原交错区的景观格局动态模型

（一）背景

景观格局是指大小和形状不一的景观斑块在空间上的排列形式，景观空间格局分析是探讨景观格局和生态过程相互关系的基础。近年来，随着景观生态学的不断发展，景观格局及其动态研究已成为景观生态学研究的热点和重要领域。生态交错带（Ecotone）又称生态过渡带，是特定尺度下生态景观实体之间的过渡带，是存在于相邻的不同均质景观单元之间的异质性景观。对于生态交错带内的景观格局的研究，是揭示其生态环境状况、空间变异特征以及生态过程相关的区域资源环境问题的有效手段。现今，国内有关森林——草原交错区景观结构、功能特征以及动态变化驱动力分析的案例还较少，交错区景观变化的方向和速率，未来景观变化的趋势以及到目前为止已采取的各项有关森林、草原的保护政策、措施在该区域景观变化中的成效如何，这些问题都还没有一个系统的研究。刘立成等通过1988—2004年期间，研究区内各景观类型之间的面积转移规律与景观格局指数变化特征，系统地分析了该区景观格局时空动态的变化趋势，旨在揭示外界干扰与该区景观动态变化之间的关系以及该区景观格局演替发展的规律。

（二）公式

1．景观格局变化动态度模型。

动态度是指某研究区一定时间范围内某种景观类型的面积变化程度和速率，其表达式为：

式中：S为研究时段某一土地利用类型动态度；Ua、Ub分别为研究期末某一种土地利用类型的面积；T为研究时期。

2．景观格局空间变化模型。

土地利用的空间变化，可用土地资源分布重心变化情况来反映。同样，这种方法可以应用到景观类型空间变化中来，其方法为分别求出四期景观分布图中各景观斑块的质心坐标，然后乘以各个景观斑块的面积，最后把乘积累加后除以同期全区该区域该景观的总面积。

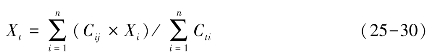
式中：Xt、Yt分别表示第t年某种景观类型质心的经度、纬度坐标；Cij为第t年该景观第i个斑块面积；XiYi分别表示该景观第i个斑块的经度、纬度坐标。

3．景观格局特征指数。

研究景观格局特征一般在三个层次上进行分析：单个斑块级别上的分析（pach⁃level），研究内容有斑块的大小、形状、周长；斑块类型级别上的分析（class⁃level），反映的是景观中不同类型的结构特征，包括各种景观类型的斑块密度、大小、周长等；景观级别上的分析（landscape⁃level），研究内容有景观多样性、镶嵌性、破碎度和优势度等。刘立成等借助于Fragstats 3．3软件，着重从类型级别和景观级别出发，对研究区的景观格局指数变化作出了系统的分析，研究选取的评价指标及其意义见表25-1。

表25-1　景观格局指数说明

注：i，j代表景观类型；n为景观斑块数；A为景观总面积；P为景观斑块周长；a为景观斑块面积；c表示景观类型的个数；m为景观类型总数；V代表最大斑块面积；C为景观的破碎度；F为景观的分离度；MPFD代表平均斑块分维数指数；N为景观中斑块总数；LSI代表形状指数；SHDI为多样性指数；LPI为最大斑块数；E为均匀度指数；D代表优势度指数。

（三）意义

刘立成等研究结果表明：1．16年来，呼伦贝尔森林——草原交错区各景观类型转换频繁。其中，林地面积减少量最多，达7 858．15 km2，主要转换为草地；未利用土地面积增加量最多，净增4 087．25 km2，增加的面积主要来源与草地和林地。2．景观格局整体波动较大，景观破碎度、景观多样性指数逐年增大，优势度指数降低。3．受人为干扰的影响，研究区内各主要景观类型均表现出景观斑块由大到小，由少到多，斑块形状复杂化程度增加的特点。其研究结果可为今后制定各种相关方针政策，合理管理开发利用交错带内资源，保护生态交错区的功能，维护交错区可持续发展提供重要的科学依据。

二、土壤水分的时空分布模型

（一）背景

黄土高原地区土壤水分布受地形、土地利用等众多因素的影响，而现有的土壤水分模型大多针对局部的点或一个坡面的土壤水分以及农田水分进行研究，难以对复杂地形下的区域土壤水分空间分布进行预测，因而不能为植被的空间布局提供科学依据。GIS和人工神经网络（ANN）中的BP网络模型为分析土壤水分空间分布的不确定性及复杂性提供了有效处理手段。人工神经网络模型可模拟各因素之间的非线性关系，并可在GIS支持下将模型推广到区域空间范围。赫晓慧等对黄土丘陵沟壑区不同植被与地形条件下的土壤水分空间演变模型进行了研究，已达到模拟黄土高原土壤水分时空分布的目的。

（二）公式

BP算法实际上是前向式多层网络的实际输出与要求输出之间最小均方差的一种迭代递度算法，即用网络的实际输出与目标之间的误差来修正其权值，使目标输出与目标期望值尽可能地接近，就是使网络输出的误差平方和达到最小。BP算法由两部分组成，即信息的正向传递和误差的反向传播。在正向传递过程中，输入信息由输入层经隐含层逐层计算传向输出层，每一层神经元的状态只影响下一层神经元的状态。如果在输出层没有得到期望的输出，则计算输出层的误差变化值，然后转向反向传播，通过网络将误差信号沿原来的连接通路反向传播回来，修改各层神经元的权值，直到达到期望目标。

设输入为p，输入神经元有r个，隐含层内有s1个神经元，输出层内有s2个神经元，对应的激活函数为f（x），输出为a，目标矢量为T。则隐含层中第i个神经元的输出为：

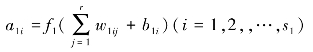
激活函数f（x）一般采用Sigmoid模型，即：

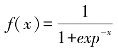
输出层第K个神经元的输出为：

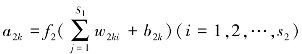
在满足一定精度要求下一般取较小的数值，以改善网络的概括推论能力，在训练中网络的收敛采用输出值与实测值tp的平均绝对误差进行控制，其误差E（W，B）和训练样本集误差E可分别定义为：

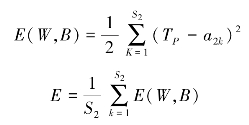
以上为网络学习的信息正向传播过程。另一个过程为误差的反向传播过程，当误差大于期望值时，则将误差反向传播，利用梯度下降法调节权值的变化：

式中；Δw（i）为i次训练时权值和域值的修正；η，α分别为比例系数和动量系数。

（三）意义

BP神经网络模型考虑到了时间和地形、植被等对土壤水分空间分布的影响，结合精确的DEM，利用非线性模型而不是固定的经验值表达土壤水分的时空间分布，使得寻求区域土壤水分时空间分布规律成为可能。该模型能更好地描述土壤水分分布的复杂非线性特性，不需要建立具体的数学模型，计算相对简单，是一种建立能反映土壤水分变化与其主要影响因子之间非线性关系模型的好方法。

三、森林植被的林窗模型

（一）背景

森林动态是指一个地区的森林植被、动物区系、土壤和小气候等，随着时间的推移而发生的各种变化过程，这种变化在许多森林内呈现为一种循环的模式。从19世纪后期到20世纪50年代，人们对森林植被动态的研究，主要侧重于对演替过程的描述和演替理论的发展。20世纪50年代开始了以模型的方式研究森林动态。Dale把森林动态模型划分为两类，森林生长模型和群落动态模型。森林动态模型中理论体系比较完整，在实践中应用最成功的是林窗模型。林窗模型是建立在森林循环动态理论上，模拟林分内单木动态变化的模型，主要用来模拟木本植物占优势的群落，并得到较好的结果。桑卫国等用林窗模型研究了小兴安岭南坡红松针阔混交林长期动态变化过程。

（二）公式

林窗模型是通过模拟某种森林的一系列空间不相连样地来了解森林的特性，这个过程的原理同森林抽样调查类似。每个样地由一到多个树种的个体组成，每株树由树名、胸高直径、枝下高（从林地表面到树冠基部的高度）、叶面积和年龄来表示。设定样地内的资源（光照、水分、养分等）在水平空间均匀分布，样地内的个体与其他个体通过资源利用产生竞争和相互影响。通过计算光在林冠层的传播直接模拟林分的垂直结构。

林地面积直接影响到林分内的叶面积和生物量状况，叶面积和生物量决定样地内的环境因子变化特点，因而样地面积是决定模拟结果和演替模式的最重要参数。小样地内，成熟木的死亡会引起样地叶面积和活生物量的较大变化，引起环境因子极大波动。大样地内，单木的影响很小，林窗现象不明显。根据以往林窗模型样地面积设置和红松林特点，本模型把样地面积设为0．1 hm2。

模型输出包括森林的结构特征（林木大小分布、垂直结构）和总体特征（树种组成、断面积、生产力和生物量）。

在林分水平上，模拟林木对空间、光和其他资源利用产生的竞争与生长、更新和死亡的关系，树种在这些过程中的竞争地位取决于个体利用资源的特点。生长用计算个体直径生长量的确定性函数表示，更新和死亡用以林分状况和树种遗传特性得出参数的概率函数计算。模拟的时间间隔定为1年。

1．更新。

更新通过以下过程实现，首先根据模拟样地的叶面积指数计算林地地表的光强，然后与所有树种的光补偿点参数相比，如林地光强大于树种的补偿点，则该树种能在林下更新，更新数量由给定更新强度的泊松分布计算出，根据FOR⁃SKA模型把更新成功的幼树胸径和叶面积赋给一个较小的值，枝下高和年龄设为0。

2．生长。

光是影响树木生长的最主要因子，对它的模拟是林窗模型的主要内容之一。在林冠层中光从上至下逐渐减弱，这个过程遵循朗伯-比尔定律，表示为

式中，I（0）为林冠层上部的有效生理辐射，I（z）为冠层深处z的有效生理辐射；K为群落的消光系数；L（z）为模拟样地中所有林木高于z出的累积叶面积指数。林冠层上部的有效生理辐射是纬度和日照率的函数，大多数森林群落取值在300～600 μmol·m-2·a-1之间。消光系数在森林群落种的取值一般介于0．3～0．6之间。

光强直接影响林木的同化作用，林冠不同深度处光强不同，因而同化作用率也不同，同化作用与光强的关系用光反应曲线表示，这个函数形式与酶促反应的米切利斯-曼顿渐进函数相近，函数表示为：

式中，p（z）为林冠层z处叶的同化作用率；KI（z）为该层平均有效生理辐射吸收率；c为树种的光补偿点（光合作用固定的二氧化碳等于呼吸作用释放的二氧化碳时的光照强度称为树种的光补偿点），为树种的光半饱和点（树种净同化率达到其最大值一半时的光强）。参数c和与树种的耐阴性密切相关。

单木的年生长量等于树木1年的净同化作用量，通过累加从树梢到树冠基部同化量与呼吸量之差得出。生长量yoga测树学的材积指数D2H表示，函数形式为：

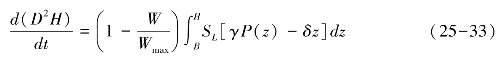
式中，D为胸高直径；B为枝下高；H为树高；SL为树冠层叶面积线密度；γ和β为与树种有关的表示同化作用和呼吸作用的参数；W为模拟样地的生物量；为该森林群落的最大生物量。假设树叶在树干上均匀分布，则叶面积线密度为SL＝L/（H-B）。树干材积转化为生物量可以通过下面关系方程计算：

式中，q为所有树种生物量转换因子，这个常数与地区的木材密度和温湿度等有关。

树高计算同其他林窗模型相同，首先计算出林木的材积指数，然后通过直径生长方程得出直径生长量和直径，用高径关系方程计算树高，高径关系方程表示为：

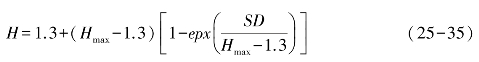
式中，Hmax为最大树高；S为常数

根据管道模型理论，单木叶面积同树干边材面积成正比，幼树没有心材，得到幼树叶面积方程：

式中，C为与树种有关的常数，用幼树的胸高断面积与叶面积之比得出。

管道模型原理认为随着树木的生长，边材逐年向心材转化，根据实际数据分析结果可算出边材向心材的年转化率tSW，这样得到单木叶面积年变化方程为：

以方程（7）计算出叶面积年生长量加上前一个生长季叶面积得出本生长季叶面积。

3．死亡。

林窗模型中树木死亡以两种方式出现：与树木寿命有关的死亡，假设某一树种只有1%的个体能达到其最大年龄，死亡率计算方程为：

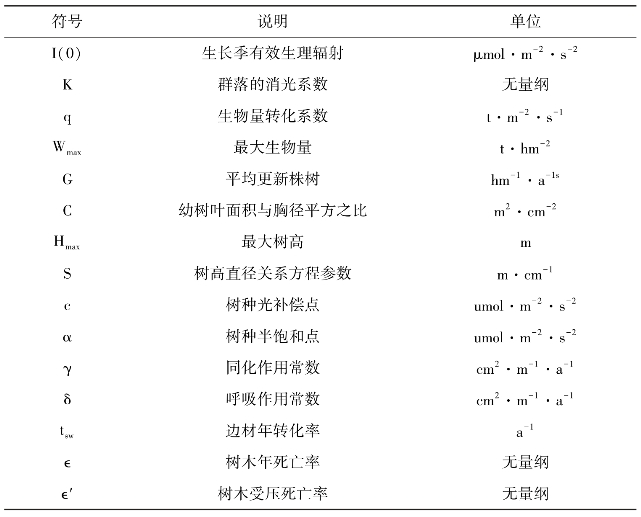
式中，M0为年龄n时树木死亡概率；ε为树木死亡率；n为树木年龄，竞争引起的死亡，生长状况不好的树木死亡率增加，树木直径生长量小于0．01 cm时的死亡率，用林木直径生长连续小于这个值存活的年数来确定，考虑到树种的耐阴性特点和林窗模型中枯死概率参数的不灵敏性，本模型设定红松、云杉和冷杉等耐阴的树种20年后存活率为1%。模型的参数说明及定义见表25-2。

表25-2　模型参数表

（三）意义

桑卫国等用林窗模型研究了小兴安岭南坡红松针阔混交林长期动态变化过程。通过有效性检验证明所得模型能够合理地预测森林的组成、结构和动态。以经营数据估计模型的参数后，运行模型模拟12个树种600年的演替动态，结果表明，次生裸地的森林在几个世纪后能恢复到以红松为主的针叶树占优势的群落，演替呈现为树种组成差别很大的3个阶段：第1个阶段为0到70年，这时阳性先锋树种在群落中占据优势，无论树种组成，生物量，生产力，阳性树种占的比例都最大；第2个阶段为70-300年，在这个阶段中，硬阔叶树占优势，呈现了树种多样性最大的一个阶段，阳性阔叶树种还未退去，耐阴针叶树种已开始增多；第3个阶段为300a后，针叶耐阴树种开始在群落中占据优势，并且整个群落的树种组成、生物量和生产力变化很小，林分的各种特征呈现一定波动的相对稳定态。

四、沙地草地的土壤水分平衡模型

（一）背景

在毛乌素沙地区，由于沙对地表蒸发的阻滞作用，盐碱的问题不甚明显，而水分作为限制因子其问题则非常突出。高效、合理地利用自然降水，成为沙地植被发展及资源利用的关键。沙地草地生态系统模型的研究在近年也有所进展。但这些多变量、多参数的复杂系统模型终因沙地立地条件和植被的恢复性及定量信息的缺乏，而难以在短期内取得精准的分析结果。高琼等以简单的水分平衡模型为基本手段，力求利用现有的沙地植物生理生态研究资料来完成模型的参数化工作，使分析结果具有较高的准确程度。

（二）公式

考虑一坡向为A，坡度为a的坡面，其地表的植物覆盖率为C，植被覆盖率为1．0时的叶面积指数为Lai（t），t为时间。这样地表的表观叶面积指数Lai（t）′＝（t）。定义土壤表面的入渗系数又为降水渗入土壤的速率与降水速率之比，并以λv和λs分别表示植被覆盖部分地表和无植被覆盖部分地表的入渗系数。λe和λs除与土壤的物理特性有关以外，还与坡度有关，在0-π/2范围内，坡度越大，入渗部分就越小，而形成同流的可能性比较大。更具体地说，鉴于入渗是由于中立的作用结果，λv和λs可以写成重力势的函数。由于植被覆盖部分的地表结皮的作用，因此，凡除描述了植被对入渗的阻滞作用外，更主要的是反映了植被覆盖部分的地表结皮对入渗的阻常作用。所以，一般应有λv＜λs以P（t）和E（t）分别表示降水和叶面积指数为1时的可能蒸腾强度，实际蒸腾强度为CLai（t）E（t）。由于坡度的作用，地下潜流可表示为土壤水分W（地表2 m深度以内的土壤水分），由于植物根系的持水作用所形成的阻滞系数r，植被盖度C及坡度a的函数，即g（C，r，W，a）。在忽略地表蒸发的情况下，可以写出瞬时的土壤水分动态方程为

模型的结构如图25-10所示。图中虚线箭头代表信息流动方向，而实线箭头代表物质或能量流动方向。土壤水分W有下界Wmin，由土壤最小持水量所决定；在上界Wmax由土壤的饱和含水量所决定。以下就模型中的各函数和参数的确定展开讨论。

1．入渗系统λv和λs的确定。

入渗系统主要由土壤的导水特性和坡度所确定。考虑坡度为0时的无限薄的土壤表层的入渗情况，可以写出：

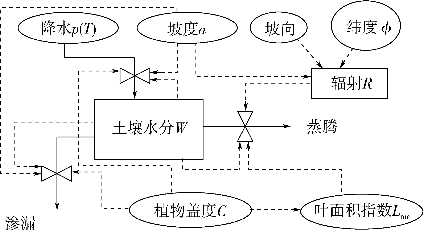
图25-10　沙地草地水分平衡关系示意图

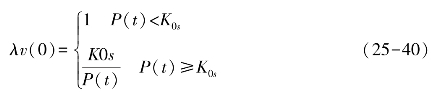
式中，K0s为植被覆盖地表所形成结层后的饱和导水率。

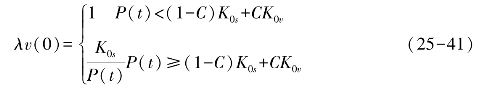
假定无植被覆盖地表与植被覆盖部分均匀镶嵌，则当P（t）＞K0v时，植被覆盖部分有环流产生。这部分通流与P（t）相加，形成无植被部分的有效降水。所以，根据对沙地草地土壤的导水实测的结果，可以初步确定，K0s在1 000 mm/月，K0v＝70 cm/月左右。在坡度不为0的情况下，λv（a）＝λv（0）cos（a），λs（a）＝λs（0）cos（a）。因此，在坡度为零的情况下，只有在降水的瞬时速率大于（1-C）K0s＋K0v时，地表才可能有通流产生。当植被覆盖率为1．0时，瞬时降水速率超过1 000 mm/月，当植被覆盖率为0．5时，瞬时降水速率须大于5 350 mm/月才可能有通流产生。对植被覆盖率较低，土壤沙性较重，而降水少的毛乌素沙地来说，除在坡度较大的梁地上外，形成通流的可能极小。由此可见，沙地因结皮所产生的通流量在全年降雨中所占的比重极小。只有在某些坡度较大的硬梁或土质具较大黏性的软梁地上（此时尺K0v较小），地表通流才占有相当的比重。

2．叶面积指数Lai（t）。

根据大多数沙地草地的植物物候，植物叶面积指数在5月初开始有明显上升，至6月中达到最大值，并一直维持到9月初。此后叶面积指数下降，至10月初活叶面积指数降至近似为。据此可写Lai（t）的函数形式Lai（t）＝L0V（t）。其中L0是与植被类型（或群落类型）有关的常数，而V（t）为峰值为1的梯形函数，即

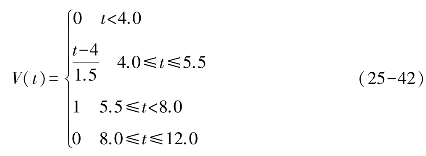
根据实测得的毛乌素当地的蒙古岩黄芪的叶面积指数，可算出L0在1．966～3．30间。

3．潜在蒸腾E（t）。

考虑坡度为a，坡向为A的坡面上的植物蒸腾耗水情况。可将E（t）写成E0ε（t），其中E0为常数，ε（t）为极大值1时与辐射成正比的函数。当太阳高度角为h、方位角为a时（方位角a、坡向A均以正南为0度，地图平面上顺时针方向为正），

式中，h和a与地理纬度Φ、太阳赤纬δ和时角Ω有关。h，a可以用普通天文公式求出。

根据实测的蒙古岩黄芪的分月蒸腾数据，用数值积分方法对方程的蒸腾项进行以月为区间内的积分（步长为2 h），即求取

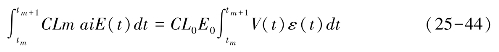
式中，［tm，tm＋1］为一个月以内的积分区间。根据实测的蒸腾值，算得E0在10 cm/月左右。

4．潜流渗漏函数g（C，r，W，a）。

潜在渗漏函数是沙坡的主要土壤水分损失之一。g应体现：土壤的最小持水量条件，即当土壤水分小于田间持水量（Field Capacity）时，潜流为0；最大潜流速率条件，即当潜流速率上升至某一特定值时，边界条件限制了潜流速率的进一步增加；根系的持水作用效应，即植被覆盖率越高，土壤中根系越多，持水能力越强的特点。由此取g为如下形式：

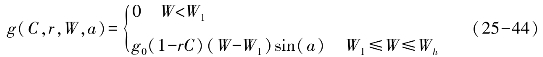
式中，g0，W1，Wh为常数；为沙地的田间持水量。沙地土壤的田间持水量一般很小，以体积含水率0．05计，可以近似取＝10 cm。由于缺乏数据，可认为等于其最大的持水量，即饱和含水量。以0．15计，在地表2 m以内的饱和含水量是30 cm。g0的确定可以考虑在一个生长周期内，坡度适中（30°左右）而植被的覆盖率为0时，系统处于稳定状态，年降水被全部转换为潜流（忽略沙地蒸发），这样估计得到的g0近似等于0．4。

植被阻滞系数r是最不易确定的一个系数。可以这样考虑：当植被类型为一定时，c在（0，1）区间变化时，最大、最小可能的持水效应r，C也应在（0，1）区间。这样r也应在（0，1）区间。r取0值表示植被完全不能帮助土壤持水，反之r＝l则说明当植被的覆盖率为l时，植被完全抑制了潜流的产生。这两种情况都不符合实际的极端情形。

5．降水函数P（t）。

降水是生态学研究中随机性最强的量之一。但由于髙琼等只关心多年的平均效应，故拟以近似的方式来确定降水：假定降水完全集中于6-8月，以P（t）＝P0Ψ（t）来表示（P0为常数），且

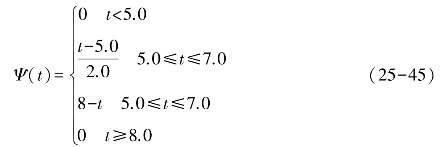
以年降水为350 mm计，可推算得P0＝23．3 cm/月。

6．土壤水分的上下Wmax和Wmin。

假定考虑的是地表2 m的土壤层内的土壤水分的含量，且最小的含水率为1．5%，饱和含水率为15%，这样有Wh＝Wmax＝30 cm，而Wmin＝3 cm。

（三）意义

高琼等从土壤水分平衡出发，用动态仿真模型方法研究我国北方干旱半干旱沙地草地土壤水分平衡与立地条件，如坡度、坡向、土壤物理性状及植被覆盖率之间的关系，有如下初步结论和论点产生：1．地表因植被的存在而形成的结皮对降水入渗到土壤中的阻滞作用几乎可以忽略。只有在坡度很大，瞬间降水强度很大时，结皮表面才可形成较大的迁流。2．土壤水分的平衡随植被的覆盖率变化的情况（上升或下降）取决于立地条件的差异，笼统地讲“植被覆盖率越高越好”或“植被覆盖率一概不宜太高”未免失之偏颇。

五、优势种间的联结性计算

（一）背景

伏牛山国家级自然保护区位于中国东部亚热带和暖温带的过敏区，植被优势种明显，以灌木优势种为主体进行植物功能群分类，可以对森林生态系统的功能、框架结构及类群分布有一个明确的认识。胡楠等采用群落生态学的调查方法，在伏牛山南北坡设置66个典型样方。根据调查结果，通过计算重要值，选取优势度相对较大的灌木树种进行种间联结及相关性分析，以χ2（卡方）检验为基础，结合联结系数AC和共同出现百分率PC来测定灌木优势种间的联结性，根据优势种间的联结性及其在海拔梯度上的变化异同来划分植物功能群。

（二）公式

选取优势度相对较大的灌木树种进行种间联结及相关分析。建立2×2联列表，并根据原始资料矩阵，计算各种对的a、b、c、d值。以χ2检验为基础，结合联结系数AC和共同出现百分率PC方法共同测定物种间的联结性。

1．检验两个种关联与否一般用χ2检验。

由于取样为非连续性取样，因为，非连续性数据的χ2值用Yates的连续校正公式计算：

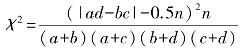
式中，n为取样总数，a为两物种均出现的样方数，b，c分别为仅有1个物种出现的样方数，d为两物种均未出现的样方数。当ab＞bc时为正联结，ab＜bc时为负联结。若χ2＞3．841（0．01＜p＜0．05）则表示种对间联结性显著，若χ2＞6．635（P＜0．01）表示种对间联结性极显著。

2．联结系数AC。

联结系数AC用来进一步检验由χ2所测出的结果及说明种间联结程度。其计算公式如下：

若ad≥bc，则AC＝（ad-bc）/［（a＋b）（b＋d）］

若bc＞ad且d≥a，则AC＝（ad-bc）/［（a＋b）（a＋c）］

若bc＜ad且d＜a，则AC＝（ad-bc）/［（b＋d）（d＋c）］

AC的值域为［-1，1］。AC值越趋近于1，表明物种间的正联结性越强；相反，AC值越趋近于-1，表明物种间的负联结性越强；AC值为0，物种间完全独立。

3．共同出现百分率PC。

共同出现百分率PC也是用来测度物种间正联结程度的，其计算公式为：

PC＝a/（a＋b＋c）

PC的值域为［0，1］，值越趋近于1，则表明该种对的正联结越紧密。

（三）意义

种间联系法可以研究种树种间的联结性强弱，为划分功能群提供了一个很好的依据。

六、NPP和理论载畜量的估算公式

（一）背景

玛曲县是黄河上游重要的水源补给区，补给水量达黄河上游总水量的45%。近些年来，玛曲草地严重退化，水源补给量减少，特别是黄河沿岸地区出现了片片黄沙，对黄河流域的生态安全造成了重大影响，为此受到广泛关注。大量研究表明，全球气候变化和人为因素的影响是构成草地生态环境恶化的主要驱动因素。张龙生等运用遥感与地面调查相结合的方法，查清了玛曲草地沙化的面积，并认为沙漠化是自然与人为因素共同作用的结果，以过牧为主导因素。研究表明，过牧造成了玛曲草地生态系统服务价值的大量损失，玛曲草地的沙化是一个多因素综合作用的复杂过程，在缺乏长期定点观测和试验的情况下，基于气候-草地-牲畜系统动态变化特点，建立一个理论分析程式，确定引起草地沙化的主导因素并量化其作用程度，为调整草地生态系统管理的政策提供科学依据。

（二）公式

1．草地植被NPP的估算。

采用周广胜模型来估算玛曲草地的NPP，该模型考虑的因素比较全面，有降水、温度、辐射干燥度、可能蒸散量等，估算的结果较好。模型如下：

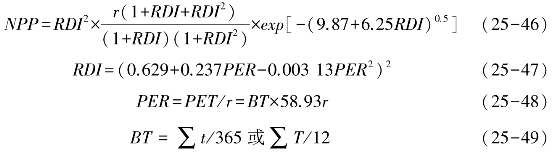
式中，NPP为自然植被的净初级生产力［t（DW）/（hm2·a）］；RDI为辐射干燥度；r为年降水量（mm）；PER为可能蒸散率；PET为年可能蒸散量（mm）；BT为年平均生物温度（℃）；t为≥0℃与≤30℃的日均温度；T为≥0℃与≤30℃的月均温度。

2．理论载畜量的估算。

基于可利用的NPP总量能养活的牲畜数量，用上述模型估算出单位面积的NPP后，可用下式估算理论载畜量：

式中，Lt为第t年的理论载畜量（羊单位）；Ag为草场面积（hm2）；Adt为第t年的沙化面积（hm2）；NPPt为第t年的单位草场面积的总干物质产出（kg）；r为M的地上部分可利用率。NPP中地上部分与地下部分之比为9∶11，牧草利用率取50%；g为一个羊单位日食干草量（kg），其标准取2．0 kg干草。

3．草地超载量的估算。

理论载畜量计算出后，各年超载量可用下式计算：

式中，Lni是超载量（万羊单位），Li是理论载畜量（万羊单位），Lf是实际载畜量（万羊单位）。

（三）意义

玛曲草地沙化是自然因素和人为因素综合作用的结果。通过分析降水、温度、日照、风、土壤几个自然因素，结果表明：影响玛曲草地沙化的自然因素主要是温度升高，特别是不小于0℃积温的增加。对草地产生不利影响的人为因素有放牧、垦荒、挖药取薪、采金、偷猎以及修路等。与持续放牧相比较，其他人为因素的影响是局部的、非连续性的。因此驱动草地退化的人为因素主要是超载过牧。基于草地NPP及其利用率的估算，可以计量草地的理论载畜量和超载量。随着气温升高，玛曲草地总NPP和理论载畜量在波动中缓慢上升。但50多年来玛曲草地的实际载畜量持续上升，从低于理论载畜量到超载过牧，草场压力不断增大。超载量在2000年达到最大值，超过理论载畜量106．25%。用生产函数分析温度升高和超载过牧对草地沙化的作用程度，结果表明，温度升高的影响占34．39%，超载过牧占65．61%。草地、沙化是过牧的累加效应达到一定程度时才出现的，累加超载量每增加1万个羊单位会造成3．14 hm2草地沙化。表明草地生态系统具有一定的抗干扰能力。草地沙化的防治应以草畜平衡为基础，降低载畜量，逐步减少超载量的累加。

七、农牧区系统的区域差异评价指标

（一）背景

农牧区系统的区域差异研究是制定种植业与养殖业协调发展计划与规划的基础。过去由于侧重于对种植业和养殖业进行系统区域差异分析，所以在一定程度上难以适应种植业与养殖业协调发展的要求。为此，张伟建等对长江三角洲集约农牧区系统进行调研及综合分析，研究探索该农牧区系统种植业与养殖业协调发展的内在规律及其发展趋势。

（二）公式

不同农牧区系统是在其自然资源背景及社会经济条件共同作用下形成的，具有不同区域特征，一定区域范围农牧系统内种植业与畜牧业相辅相成。因此，农牧系统评价指标体系应从自然资源背景、种植业与养殖业结构及社会、经济多方面因素综合考虑。

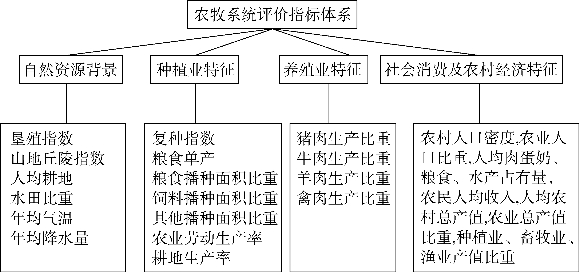
图25-11　农牧系统评价指标体系

根据已确定的评价指标，对调查、收集和整理的原始数据建立分区样本矩阵X。因土地利用现状评价涉及因素众多，且各自量纲不一，数值相差大，故在分区前应进行数据标准化处理。经计算比较，用极差规格化比较适宜。原始数据经标准化后获得分区样本标准化矩阵X′，其数学模型为：

获得分区样本标准化矩阵后，先定性确定预分区数，并采用均差法计算全部样本的重心Gkj及各指标的标准差Sj。以各重心为凝聚点，计算各评价对象与凝聚点间的欧氏距离dik，根据距离进行分类。

（三）意义

长江三角洲集约农牧区系统区域差异评价指标体系，包括自然资源状况、种植业与养殖业特征和社会消费与农村经济特征等方面内容。对指标体系进行动态聚类分析，根据农牧系统的主要特征，预测长江三角洲集约农牧区系统及其发展趋势。

八、森林碳汇的功能模型

（一）背景

大气中CO2等温室气体浓度逐年增加，“温室效应”所导致的全球气候变化已引起世界各国的普遍关注。

森林是陆地生态系统的主体，森林在生长过程中丛大气中吸收并固定大量的CO2，森林的采伐和破坏又将其储存的释放到大气中。因此，森林既可能成为汇，又有可能成为源。对森林的汇或源的作用作出定量的评价和估计，对于制定减缓排放的有效措施具有重要的意义。

（二）公式

1．木材消耗模型。

生产建设用材需求量可以用木材消耗强度法，根据国民经济发展趋势进行预测。所谓木材消耗强度是指一定时期内国民经济各部门生产单位产品所消耗的木材数量。木材消耗强度法的基本公式为：

式中，Q为木材的需求量；G为国民经济各部门的产品总量；r为经济增长率；R为木材消耗强度；γ为木材消耗强度的增长率；0、t分别为基期和预测期。其中，木材消耗强度增长率γ可以通过测算木材消耗弹性E来确定。这里木材消耗弹性是指国民经济产品总量变动引起的木材消耗量的变化率。它与木材消耗强度增长率的关系为：

设预测基年生产建设用材年需求量为Q0，并假设预测期内国民经济稳定增长，年递增6%～7%，木材消耗弹性保持在0．25-0．3之间，则预测期内木材消耗强度增长率为：

相应的预测期内第七年的生产建设用材的年需求量为

表明预测期内生产建设用材的年需求量将以1．336%的增长率逐年递增。与生产建设用材的需求量相比，人民生活用材的需求量增长缓慢。其增长率主要由农民造访和烧柴的需求量所决定见表25-3。对这两项年需求的预测结果可推算出，人民生活用材的年需求量将以0．468%的增长率逐年递增，即

其中，L0和Lt分别为基期和预测期人民生活用材的年需求量。

表25-3　中国森林资源消耗结构

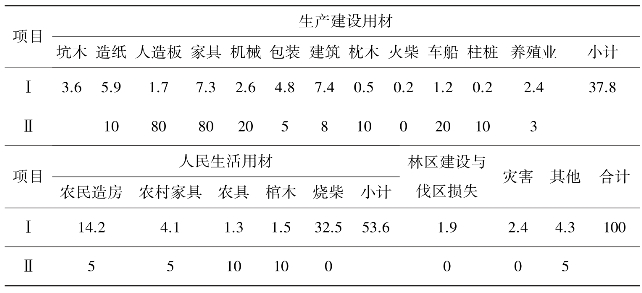
注Ⅰ：比例（%）；Ⅱ：耐用年限（a）。(www.chuimin.cn)

取1990年为基期，Q0＝0．387×32 000＝12 096，

L0＝0．536×32 000＝17 152

以表25-3作为基年的森林资源消耗结构，预测期生产建设用材和人民生活用材的年需求量为式（25-55）和式（25-56），并假定其他部分（林区建设、伐区损失、灾害及其他）占森林资源消耗总量的比例保持不变，可得预测期相应的森林资源消耗结构见表25-4。

表25-4　中国森林资源消耗结构预测

由表25-4和式（25-55）、式（25-56）可推出未来森林资源总需求量的预测公式

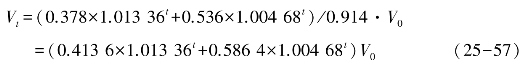
取1990年为基期，V0＝3．2×108m3，则上式成为

2．森林资源生长量预测模型。

全国森林清查资料表明，中国森林年均净生长量基本呈现线性增长的趋势。把表25-5中的林木年均净生长量分别看作各次清查的中间年份（即1975年、1979年、1986年、1991年）的林木年净生长量，可以得到如下的线性回归方程

其中，GV代表林木年净生长量（×104m3）；为时间变量（a），t＝0对应于1975年；为相关系数。式（25-59）表明，从20世纪70年代至今，全国林木的年生长量平均每年增加0．106 9×108m3。

表25-5　中国活立木蓄积消长统计

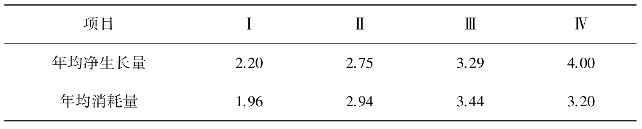
注：Ⅰ：第1次清查（1973—1976年）；Ⅱ：第2次清查（1977—1981年）；Ⅲ：第3次清查（1984—1988年）；Ⅳ：第4次清查（1989—1993年）。

为了方便，将预测基年（t＝0）改为1990年，用t＝15代替式（25-59）中的t可得到中国森林资源年生长量预测公式

GVt＝38 350＋1 069t

3．中国森林固C量预测模型。

以1990年为基期（t＝0），利用式（25-58）、式（25-59）可预测1990年后第t年森林资源年消耗量Vt和年生长量GVt。由式（7）可以推算出预测期内第t年资源消耗总生物量为

Tt＝1．9×Vt＝25 147×1．013 36t＋35 654×1．004 68t

考虑到资源消耗的总生物量中有3．4%左右的生物量长期贮存于木制品中，不释放CO2，预测期内第t年森林资源消耗所释放的C量的预测公式应为

CEt＝0．966×0．5×Tt＝12 146×1．013 36t＋17 221×1．004 68t

预测期内第t年森林生长的固C量的预测公式为

GAt＝1．9×0．5×GVt＝36 433＋1 016t

由此得到预测期内第t年的净固C量的预测公式

CANt＝CAt-CEt＝36 433＋1 016t-12 146×1．013 36t-17 221×1．004 68t

而从基期到第t年后的C累计净固定量的预测公式则为

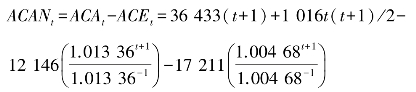
据近似公式

1．136t＝（1＋0．013 36）t≈1＋0．013 36t

1．004 68t＝（1＋0．004 68）t≈1＋0．004 68t

由此可得，预测期内第t年C的净固定量近似为

CANt＝7 066＋773t

即未来中国森林年净固量将增加773×104t/a

（三）意义

康慧宁等建立了中国森林C汇功能基本估计模型，根据森林资源消长状况和未来变化趋势，对中国森林固C的现状和潜力进行了估计和预测。结果表明，中国森林目前C积累高于C释放，年平均净固C量为0．862 7×108t/a，在未来20年内中国森林净固C能力月增加773×104t/a。到2000年，中国森林固C能力将达到1．469 7×108t/a。

九、草地枯枝落叶中氮、磷、钾变化模型

（一）背景

在草地上，植物从土壤中吸收的营养元素由于植物的枯死，大部分以枯枝落叶的形式储存在地表，并随着枯枝落叶的分解而不断地损失归还于土壤，特别是氮、磷在枯枝落叶中的变化直接影响着草地土壤的营养状况。郭继勋等对羊草草地氮、磷、钾在枯枝落叶中的动态进行了定量分析，并建立了动态模型。

（二）公式

根据枯枝落叶中氮、磷、钾的输入量和损失量，对其营养元素的动态进行分析。设在无人为干扰条件下，3种元素的输入量和输出量为恒定，其在枯枝落叶中的变化动态见图25-12。

图25-12　营养元素在枯枝落叶中变化动态模型

式中，U为营养元素的输入量；X为营养元素在枯枝落叶中的状态变量；Y为营养元素的输出量。

那么营养元素在枯枝落叶中的变化率可为：

此方程的通解为：

当t＝0时，（t）＝X（0）；C＝U/K-X（0），其特解为：

将氮、磷、钾的年输入量、年输出量、在现存枯枝落叶中的含量及传导函数见表25-6代入方程（25-63），以年为单位，可预测氮、磷、钾在枯枝落叶中的动态变化见图25-13。

表25-6　氮磷钾的输入量、状态该变量、输出量及传导函数

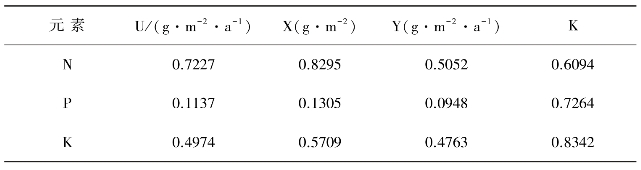
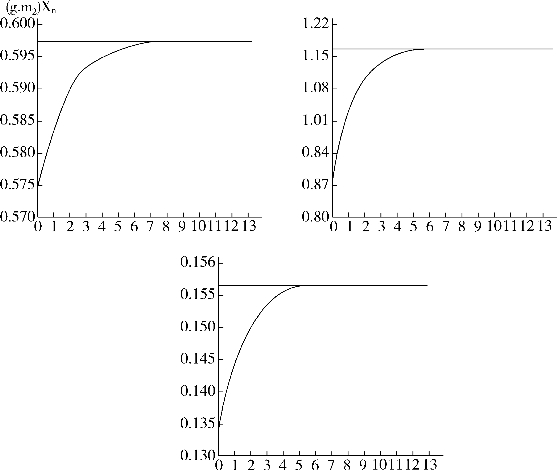
图25-13　氮磷钾在枯枝落叶中的动态分析

（三）意义

郭继勋等采用直接收集法测定枯枝落叶的年输入量，用凋落物收集器逐月测定植物的枯死量。枯枝落叶的分解采用尼龙网袋法，测定其分解速率并计算出其损失量。然后对当年枯死体及不同分解时期的枯枝落叶中的氮、磷、钾含量进行分析测定，确定各营养元素向枯枝落叶中的输入量及自枯枝落叶中的损失率。建立草地枯枝落叶中氮、磷、钾变化模型，为深入研究氮、磷在枯枝落叶中的变化影响着草地土壤的营养状况这一问题中提供数学模型。

十、荒漠绿洲植被的景观格局模型

（一）背景

荒漠绿洲植被变化是绿洲荒漠化与绿洲化过程的最直观表征，而不同时期荒漠绿洲景观格局又明显地影响或制约着荒漠绿洲植被的演变。利用植物生态学和景观生态学原理，研究荒漠绿洲植被动态，探讨荒漠绿洲植被动态与景观格局间的耦合关系，对保护和恢复自然植被，治理荒漠化并预测其发展趋势都是十分重要的。赵成义等利用观测获得的参数，研究了荒漠绿洲植被的变化，分析了景观格局的形成与功能对植被变化的影响，并进一步探讨了二者的耦合关系。

（二）公式

以1∶5万地形图为基础信息源，结合土地利用现状图、土壤图、草场图，以植被、土壤、地貌和土地利用类型作为景观分类指标，先在底图上依斑块镶嵌体类型进行勾画，再用数字化仪以ARC/INFO GIS（PC3．5）软件进行数字化，编辑后作为分析用图件，最后根据格局分析指标的要求，分别建立面积、周长、边界等不同类型数据库，再用C语言依不同指标的要求编写程序，调用上述数据库，计算格局指数。在格局分析中量化指标选用：景观多样性指数、优势度、破碎度、分离度、均匀度等。

景观多样性指数：

优势度：

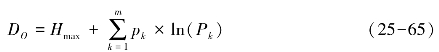
破碎度：

分离度：

均匀度：

景观斑块密度指数包括景观斑块密度PD和景观要素斑块密度：

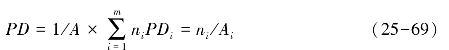
上述式（25-64）至式（25-69）中，Pk为k类景观地物所占的面积比，m为景观地物类型数目，n表示斑块数目，Ak、A分别表示k类景观面积和研究区域的总面积。斑块的分维数单斑块模型为：

多斑块模型为：

式中，P为斑块周长，A为相应斑块的面积，C为常数。

（三）意义

赵成义等总结概括了景观格局分析模型，以三工河流域为例，讨论了植被动态及其地貌、水资源利用、河流廊道和排碱渠等景观要素的变化对植被产生的影响。结果表明，随着景观格局的变化，流域内的植丛高度、盖度及生物量均表现出较大变异性。人类活动影响强烈的景观要素，其斑块多样性、破碎度、分离度和斑块密度等指数值较高，而人类活动影响较小的，其优势度和均匀度较高。为以后景观格局的研究提供理论依据。

十一、混交林物种多样性、种群空间分布格局及种间关联性模型

（一）背景

群落物种多样性是用一定空间范围的物种数量和分布频率来衡量，反映群落的环境和发育特点。空间分布格局是指种群个体在水平空间的配置状况或分布状况，反映了种群个体在水平空间上彼此间的相互关系，是由种群本身生物学特性和环境条件的综合影响所决定的。种间联结是森林群落的重要特征之一，是群落形成、演化的基础和重要的数量、结构指标，故提出混交林物种多样性、种群空间分布格局及种间关联性模型。

（二）公式

1．物种多样性的测度指标。

物种多样性采用了Shannon-Wiener指数（H′）、Pielou的均匀度指数（E）、生态优势度采用Simpson指数（D），公式分别为：

其中，S为物种数，Pi为物种的重要值。

2．种群空间分布格局。

种群空间格局分析是研究种群特征、种群间相互作用以及种群与环境关系的重要手段，是生态学研究的热点之一。选择以下聚集强度指标，判定个体在地域上分布疏密的差异程度。负二项指数K：

其中，K为负二项指数中的参数，与种群密度无关，K值越小，聚集强度越大，如果趋于∞（一般8以上），则逼近Poisson分布。扩散系数：

若C＞1，则种群分布为聚集型，C＜1，则分布为随机型，且C遵从均数为1、方差为2n/（n-1）2的正态分布。扩散型指数：

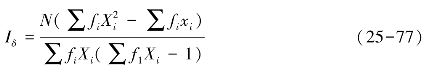
当Iδ＝1时，分布为随机型，当Iδ＞1时，聚集型分布。Cassie指标CA：

当CA＝0时，为随机分布，当CA＞0时，为聚集分布，当CA＜0时，为均匀分布。丛生指数I：

当I＝0时，为随机分布。当I＞0时为聚集分布。聚块性指标：

当M∗/M＝1时，为随机分布，M∗/M＜1时，为均匀分布，M∗/M＞1时为聚集分布。

3．种间关联度的计算。

基于2×2列联表χ2统计量来检测物种间的联结性，对于非连续性数据的χ2用Yates的连续校正公式计算，其中a为两个种均出现的样方数，b为仅有A种出现的样方数，c为仅有B种出现的样方数为两个种均未出现的样方数。

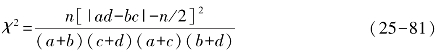
式中为小样方总数，χ2近似遵从自由度为1的χ2分布，当χ2＜3．841时，种间联结独立；当3．841在χ2＜6．635时，种间有一定的生态联结；当χ2＞6．635，种间有显著的生态联结。χ2本身没有负值，判定正、负联结的方法是当ad＞bc，种间具正关联；若ad＜bc，种间具负关联。

为进一步测定种间关联强度，采用种间联结系数AC，AC的值域为［-1，1］，种对的正关联性越强，AC值越趋近1；种对负关联性越强，值越趋近-1；AC值为0，种间完全独立。其计算公式为：

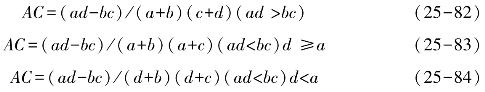
（三）意义

郭忠玲等总结概括了长白山落叶阔叶混交林的物种多样性、种群空间分布格局及种间关联性研究模型，根据在吉林省蛟河实验管理局1 hm2落叶阔叶混交林样地调查结果，对落叶阔叶混交林的群落结构、物种多样性、主要树种的空间分布格局以及树木种群的种间关联进行了研究。有助于解决群落抽样问题，预测种群消长的动态，揭示群落演替中植物替代关系的机制，为群落密度控制、群落演替趋势、植被恢复与重建提供理论依据。

十二、种群生态位测度模型

（一）背景

物种生态位研究是近代生态学理论上的一个重要内容，现代的观点认为，生态位是指在一个n维超体积中允许物种无限生存（生长、繁衍）的环境状态的组合，反映物种在群落中所处的地位、功能和环境的特性。廖宝文等采用3种常用的生态位公式和生态位重叠公式，对海南岛东寨港外来种无瓣海桑扩散区几种红树植物生态位进行初步研究，提出种群生态位测度模型。

（二）公式

生态位宽度Simpson公式：

式中：BI、BJ为物种生态位宽度，为物种i在第j个资源状态下的个体数（或重要值）占该物种在所有资源位中个体（或重要值）总数的比例，r为资源位数。

生态位重叠计测公式：

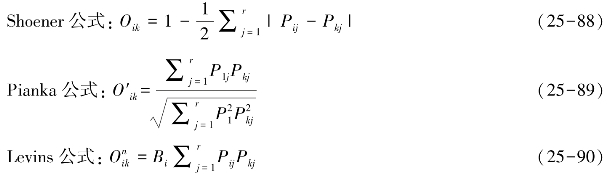
式中：、为物种i对物种j的生态位重叠值，Pij、Pki为物种i和物种k在资源序列中第j位的个体数（或重要值）总数的比例，r为资源位数，Bi为物种i的生态位宽度，因此

表25-7　无瓣海桑扩散区各群落树种个体数与重要值

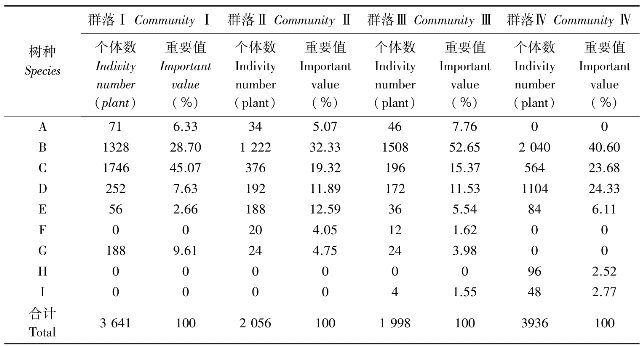
A：无瓣海桑Sanneratia apetala；B：桐花树Aegiaeras corniculatum；C：秋茄Kandelia candel；D：木榄Bru⁃guiera gymmerhiza；F：白骨壤Avicennia marina；F：红海榄Rhizophora stybsa；G：海桑Someratia caseolaris；H：海莲Briguiera sesangula；I：角果木Ceriops tagal．下同The same below．

考虑到相对重要值更能体现出树种对环境资源的利用效率，避免由个体大小差异造成的差异。因此，在对生态位宽度和生态位重叠计测时，采用相对重要值代替相对个体比例数。重要值＝（相对密度＋相对频度＋相对显著度）/300。各种群的个体数与重要值见表25-7。

（三）意义

廖宝文等总结概括了种群生态位测度模型，采用3种常见的生态位宽度和生态位重叠计测公式，以外来种无瓣海桑扩散区的秋茄＋桐花树群落演替系列作为资源轴，定量计测了几种红树植物的生态位宽度和重叠值。结果表明，各树种重叠值中，以秋茄、桐花树、木榄、白骨壤之间的生态位重叠较大，表明其间存在较强的资源利用性竞争。无瓣海桑生态位宽度处于中等程度，与中低潮滩红树植物海桑、桐花树、秋茄和白骨壤的重叠值相对较高，与红海榄、木榄有中度重叠，与角果木有少量重叠，与海莲完全没有重叠。该模型为进一步阐明外来种无瓣海桑与乡土红树植物的种间关系以及合理利用无瓣海桑提供理论依据。

十三、次生林的蒸散模型

（一）背景

森林蒸散是生态学和水文学研究的一个焦点和难点问题，不仅涉及森林生态系统的能量平衡和水分平衡，也是坡面水文过程及水量转化的重要组成。熊伟等为估计温带落叶阔叶林的蒸散量及分量，利用热扩散技术，结合微型蒸渗仪和传统水文学方法，以辽东栎、少脉椴次生林为对象，对约占六盘山林场面积60%以上的次生林进行了相关研究，旨在估计乔木树种个体水平的蒸散量及种间差异；林分蒸散量及其分量组成；探讨林分蒸散量与其结构的关系。

（二）公式

1．单株蒸散量测定。

（1）乔木：在标准地内选择生长良好的少脉椴和辽东栎样木，利用热扩散液流探头（Thermal Dissipation Probe，以下简称TDP；德国Ecommatic），在2004年8-9月连续测定了5株样木的树干液流，通过生长锥抽取样品来确定数目边材面积，最后计算出两个树种的单株蒸散量。

（2）灌木：在标准地选择主要灌木树种灰栒子和黄刺玫的单株样木，用快速称重法测定典型天气下树冠不同部位叶片的蒸腾速率，用式（25-91）计算单株的蒸腾量。

式中：Wt为灌木单株日蒸散量（mm·d-1）；EL为功能叶蒸腾速率的日平均值（g·g-1·min-1）；H为测定日实际日照时数（h）；O为天气系数，本研究晴天为1，下雨天为0，多云天气为0．7；P为叶位系数，是指同一枝条不同部位叶片日平均蒸腾速率与功能叶的比值；C为树冠系数，是指树冠不同方向和上下部位叶片日平均蒸腾速率和功能叶的比值；L为树冠总的鲜叶质量（g），这里假定其值在测定中不变。

2．单木到林分蒸腾量的尺度放大。

在测定少脉椴和辽东栎单株蒸腾量的基础上，用两个树种的边材面积为空间纯量来实现林分蒸腾量的尺度放大，具体通过式（25-92）计算乔木层的蒸腾耗水量。

式中：Ec为乔木层林木的蒸腾量（mm·d-1）；Jmean为测定样木平均的液流密度（μl·cm-2·min-1）；As-stand为单位面积上累计的边材面积（cm2·m-2）。

通过式（1）计算灌木单株的蒸腾量及两个树种在单位林地面积上的叶片总重量来计算整个灌木层的蒸腾耗水量。

3．草本层蒸散量（草本层蒸腾量＋土壤蒸发量）测定。

用自制微型蒸渗仪（φ20 cm、高30 cm）24 h连续测定其重量变化，通过式（25-93）计算草本层的蒸散量。

式中：ET为草本层蒸散量（mm·d-1）；ΔWi为第i个微型蒸渗仪两次称重之差（kg）；S为蒸渗仪的开口面积（m2）；n为测定个数。

4．林冠层截留量测定。

在标准地相隔5 m划方格线，按方格线交点布设雨量筒共8个；林外降水在样地附件空地上测定；树干茎流测定按树木径阶（按4 cm划分）进行，每个径级选1—2棵标准木，用PVC管做成的蛇形管收集树干茎流，按式（25-94）计算树干茎流量：

式中：C为树干茎流量（mm）；N为树干径级数，CN为每一径级的树干茎流量（mL）；MN为每径级树木株数；S为样地面积（m2）。最后按式（25-95）计算乔木冠层截留量。

式中：I为冠层截留量（mm）；P为大气降水量（mm）；T为林内穿透降水（mm）；C为树干茎流量（mm）。

根据公式，研究乔木层涉及辽东栎和少脉椴两个树种边材面积的确定问题，每个树种各取8株样木，同时测量树干的胸径和边材面积，分析两者关系见图25-14。结果表明，两树种树干胸径和边材面积之间存在着高度的相关关系，可以用幂函数较好地表示这种数量关系，其确定系数（r2）均达到显著。

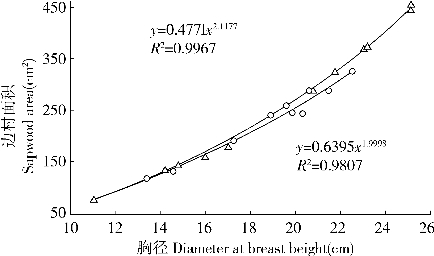
图25-14　树干胸径与边材面积的关系

（三）意义

熊伟等总结概括了天然次生林夏季蒸散模型，2004年8—9月份，利用热扩散技术，结合微型蒸渗仪和水文学方法，研究了辽东栎、少脉椴次生林蒸散组成及其与林分结构的关系。结果表明，辽东栎和少脉椴树干的液流密度在“相对静止期”内比较稳定和微弱在“活跃期内树干液流密度上升较快，并呈单峰、双峰或多峰曲线；两树种单株蒸腾量有明显的种间差异，乔木层对林分日蒸散量大小起主要作用，灌木层次之，草本和土壤蒸发量的贡献最小。为以后的研究提供了理论基础。

十四、土壤的氮循环模型

（一）背景

氮是植物必需的营养元素，也是评价土壤质量和土地生产力的重要指标。为了获得高产，需要施用大量的氮肥。土壤氮循环是氮生物地球化学循环中的重要环节，其模拟是作物估产、环境评价、农田管理、决策制度和长期预测的重要依据，对提高氮肥利用率、防止或减轻环境污染具有重要的理论和实践意义。唐国勇等拟通过简要概述土壤氮循环过程，讨论模型模拟中的参数化问题。

（二）公式

在氮循环过程模型中，通常以零级动力学方程、一级动力学方程和米氏方程等作为模型的数学基础，根据氮循环过程的影响因子，对模型进行调整和修正。零级动力学方程的微分形式可表示为：

一级动力学方程的微分形式可表示为：

米氏方程的微分形式科表示为：

其中，k0和k1分别为零级和一级动力学常数；um为最大转化速度；KS为半饱和常数；dy/dt为转化速率，Y为某N成分的含量（或浓度）。

硝化过程可用零级、一级或米氏方程进行模拟。在NTRM模型中，最初用经验的回归方程表示硝化速率：

其中，K为硝化反应速率；abc均为常数；其值分别为4．64/1．64∗10-3/0．238和-2．51；T为土壤温度；为土壤铵态氮含量；为基质硝态氮含量。经过修正，Shaffer等用机理性半阶方程来表示硝化速率：

其中，d（NH4）/dt为硝化速率；k1/2为半阶速率常数；Ea为化学自由能；kb为玻耳兹曼常数；Ts为土壤温度；NH4为土壤溶液中铵离子浓度；O2为土壤空气中氧气浓度；H＋为基质氢离子浓度。

目前反硝化过程的模拟一般采用零级或一级动力学方程，如CERES模型用一级动力学方程模拟该过程，其一级反硝化速率系数为：

其中，Kdnit为一级反硝化速率系数；Cw为土壤有机质中水提取C浓度；Wfd和Tf分别为水分和温度影响因子，h为土层厚度。CW、Wfd和Tf又可表示为：

其中，C为土壤有机质含量；SAT为土壤饱和水含量；SW为土壤含水量；DUL为土壤排干时水分含量；Ts为土壤温度。

可用零级或一级动力学方程模拟铵挥发过程，如GLEAMS模型用一级动力学方程表示该过程：

其中，r为一级铵挥发速率；CNH3为基质中氨浓度；t为时间；Kv为速率常数。该常数又可用指数方程表示：Kv＝0．409∗1．08ATP-20，ATP为气温。

（三）意义

氮既是植物必需的营养元素，又是造成环境污染的重要元素。正确模拟土壤中氮循环已经成为科学家共同关注的热点问题。唐国勇等总结概括了土壤氮素循环模型，简述了土壤氮循环的基本过程，介绍了硝化过程、反硝化过程、铵挥发过程等，并讨论了模拟中存在的参数化问题。为深入研究土壤氮循环及其模拟提供一定的参考和借鉴。