国外生态模型研究案例：生态数据分析与建模

一、种群动态增长模型

最简单的增长模型仅考虑单一种群。它与其他种群的相互作用是根据特定的增长率和死亡率来考虑的，这可能依赖于所考虑的种群的大小，但与其他种群无关。换句话说，我们只把单一种群看作状态变量。

最简单的增长模型假设无限的资源以及指数式的种群增长。可以应用简单的微分方程来表达：

式中：BS是瞬时出生率；Ms是瞬时死亡率；r＝：BS-Ms；N是种群密度；t是时间。

可见该方程是一阶动力学方程并呈指数增长。如果r是常数，积分后可得：

式中：Nt是t时刻的种群密度；N。是时间为0时的种群密度。方程（25-2）取对数后如图25-1所示。

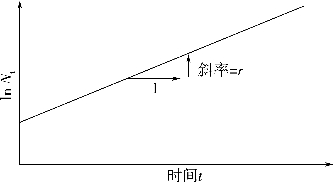
图25-1　以ln Nt对时间t作图

净繁殖率R0被定义为一个普通的新生个体在其一生中产生的年龄组为零时的后代的平均数目。存括率lx是在年龄为x时的存活分布。它是一个普通的新生个体存活到年龄为x的概率。年龄为x的一个普通个体在该年龄期间产生的后代数目，记为用mx，这称为生育力，lx与mx的乘积称为实际生育力。按照R0的定义，可通过下式得到：

lx作为年龄函数的曲线被称为存活曲线。不同物种的存活曲线有显著的差别。

所谓的内禀自然增长率r与lx和mx一样，取决于年龄的分布，只有在年龄分布稳定时，才是常数。当R0足够高时，也就是说在最适条件下并具有稳定的年龄分布时可实现最大的自然增长率，并记为rmax。各种动物的rmax可以相差几个数量级。

二、动植物种群的自疏模型

种内竞争能够影响一个种群的死亡个体数、出生个体数以及生长量。我们主要通过察看竞争的最终结果来阐明其影响。但实际上，种内竞争的影响通常是渐进的。随着种群中个体年龄的增加，个体大小及其对资源的需求也在增加，因此它们之间的竞争强度也会越来越激烈。而这又反过来逐渐增加它们的死亡风险。然而，如果部分个体死亡，种群密度和竞争强度又随之下降，并将进一步影响到种群的竞争、存活以及密度等等。

（一）动态自疏线

起初，在植物种群中的研究主要聚焦于种群密集生长的个体同生群，并关注其可能出现的变化模式。例如，以不同密度种植的多年生的黑麦草（Loliumperenne），并在种植14、35、76、104、146天后分别收获每一种植密度下的植物样本见图25-2a。线上连续的点表示不同的初始种植密度。在图25-2中，每条线都代表不同的初始种植密度，线上连续的点代表着在这一初始密密度下不同年龄的种群。因此这些线条就居同生群随时间变化的轨迹线。年处迹线上，用筒头标示出方向，从数量较多的小型年幼个体右下力指向数量较少的大型成熟个体（左上方）。

在种群密度最低时，植物的平均株重（在给定的年龄下）最大见图25-2a。那么很显然，当密度最高时，该种群将最先面临大量的个体死亡。然而最值得注意的是，最终所有同生群的密度会下降，同时平均株重随之增加：这些种群大致沿着同一直线发展。可以说，这些种群经历了自疏作用（self-thinning）（即随着种群中个体的生长，种群密度逐渐下降），其密度会发生动态变化，而在整个过程中，种群的个体干重与密度的关系趋近并服从一条直线，称为动态自疏线（dymamic thinning line）。

初始种植密度越低，自疏作用开始得越晚。在所有情况下，种群的初始轨迹线几乎都是垂直的，也就是说死亡率很小。而当它们的轨迹线接近自疏线时，种群的死亡率就会增加，然后所有自疏轨迹线的斜率逐渐接近动态自疏线的斜率，并随之变化。同样需要注意的是，按照惯例，图25-2中的x轴为密度的log值，y轴为平均株重的log值。但这并不意味着密度是平均株重所依赖的独立变量。事实上，在植物生长的过程中平均株重自然会增加，而这将导致种群密度的降低。因此，最好的说法是，种群密度和平均株重两者是完全相互依赖的。

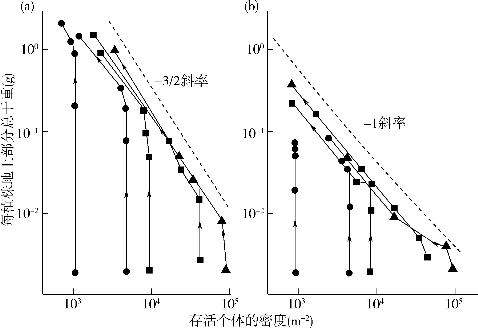
图25-2　在5个初始种植密度下，多年生黑麦草（Lolum perenne）的自疏作用

注：1000（●），5000（∗），10000（■），50000（□），100000（▲）枚种子m2。（a）0%的遮阴处理和（b）83%的遮阴处理。实验中，分别在5个时间段收货各初始种植密度下的种群，并将其用线段相连。因此它们则表示这些种群随时间变化的轨迹。箭头表示轨迹的方向，即自疏作用的方向。

植物种群（如果以足够高的密度进行种植）总会反复地接近并遵循动态自疏线。多年来，人们对所有这些线已有广泛的共识，认为其斜率大约是-3/2，这一关系常被称为“-3/2幂定律”（-3/2 power law），因此，密度（N）与平均株重（w）之间的关系可用如下方程表示：

或者

其中，c为常数。

然而需要注意的是，在使用方程25-4和25-5估计两者关系的斜率时，存在许多统计学的问题。特别是，由于w通常被估算为B/N，其中B为单位面积内的总生物量，那么，w与N必然相关，并且在一定程度上，两者之间的任何关系都具有欺骗性。因此，最好使用缺乏自相关关系的等价方程：

或者

（二）物种界线和种群界线

实际上在很多情况下，生物量与密度之间的关系并不来自随时间变化的单一同生群，而是通过对不同密度（或者不同年龄）的一系列密集种群进行比较来获得。在这种情况下，这些线更应该被称作物种界线（species boundary line），对该物种而言，密度和平均株重的不同组合是不可能在该线之外出现的。事实上，物种会受到其生活环境的影响，因此，物种界线本身可以包含一系列种群界线（pop⁃ulation boundaryline），每一条种群界线都界定了该物种的特定种群在特定环境中生存的极限范围。

因此，一个种群的自疏轨迹应该先接近而后遵循种群界线，我们称为动态自疏线——但这不一定就是其物种界线。例如，光照条件、土壤肥力、幼苗的空间分布以及其他因素都可能影响特定种群的这一界线（因此就称为动态自疏线）。例如，已有不同的研究表明，土壤肥力能够改变自疏线的斜率和/或截距。

光照条件产生的影响可以突出自疏线和界线的关键特征，因此我们需要对此进行仔细地考虑。斜率约为-3/2意味着，平均株重增加的速度比密度降低的速度更快，因而总生物量也逐渐增加（总生物量-密度图中斜率为-1/2）。但是最终一定会停止：总生物量不能无限增长。因此，我们希望将自疏线的斜率改为-1，也就是说，因死亡而丧失的生物量可能通过存活个体的生长来精确平衡，于是总生物量保持不变（总生物量-密度图中的水平线）。当黑麦草（Loli⁃umperenne）种群处于低光照强度时见图25-2b，就出现过上述情况。相比其他光照条件，在较低光照强度下，斜率为-1的界线（和自疏线）更为明显。显然，光照条件可以改变种群界线。同时它也强调，如果界线的斜率为负且比-1更小（无论是否为精确的-3/2），将意味着一定区域内的种群在达到它的最大生物量之前，其植物密度和平均株重的变化组合将受到局限。下面，我们将进一步讨论它出现的可能原因。

（三）所有物种共有单一的界限

如果将所有中的自疏线和界线划在同一张图上，会发现它们似乎具有相同时斜率，其截距（即方程25-4中的c值）也都分布在一个很窄的范围内（图25-3）。在图25-3的右下方，是浓密的爱物种群（一年生草本植物和短命的多年生草本植物），而图的左上方，是稀疏的大型植物种群，包括已知最高的植物海岸红杉（Sequoia sempervrens）。像其他领域一样，科学领域的前沿也是在不断变化的。起初，生态学家们在图25-3中发现了一致的趋势——所有植物的自疏线斜率均为-3/2，而将哪些斜率与之不同的自疏线视为“噪声”，或者对他们兴趣索然。随后，许多研究提出了不同的观点，并严重地质疑-3/2斜率的一致性以及所谓的单一理想自疏线。尽管如此，两者实际上并不矛盾。一方面，从图25-3中可见，自疏线在图形中所占比例远比随机预期的要小。显然，一些基本的现象能够将所有的类型的植物联系起来：不是一成不变的规则，而是一个潜在的总体趋势。另一方面，不同自疏线间确实存在重要的差异，它们同样需要一些合理的解释。

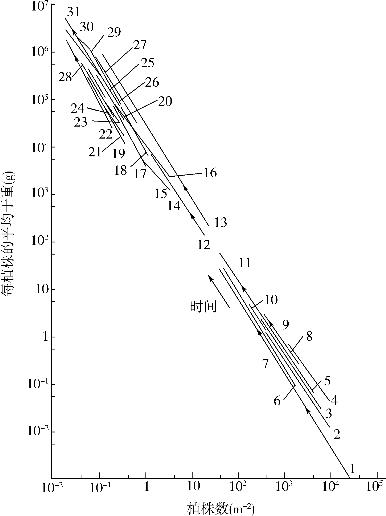
图25-3　多种草本植物和乔木的自疏作用。每条线代表一个物种，线本身的长短表示观察值的范围。线上的箭头表示自疏作用的方向。

（四）自疏作用的几何基础

于是我们开始关注这一总体趋势的可能基础，并讨论在该共同趋势下，不同物种或种群表现出差异的原因。针对总体趋势，生态学家们主要提出了两种解释。一是从几何学的角度（多年来只有这一个）；二是基于不同个体大小的植物其资源分配的差异。

从几何学的角度解释如下。在一个持续生积指数L长的植物同生群中，当种群的生物量增加时，叶面积指数（Li单位土地面积的叶面积）并不会持续增加。不管植物的密度（N）如何变化，叶面积增加到某个特定值后始终保持恒定。事实上，同样是这一临界值，在超过该值后，种群才会遵循动态自疏线而变化。我们将此表达为

其中，λ为每株存活植物的平均叶面积。然而，每株植物个体的叶面积会随着它们的生长而不断增加，因此，其平均叶面积λ也会增加。由于λ代表的是面积，因此合理地推测，它应该与一株植物的线性测量值相关，如茎干直径D，相应的公式可表达为

其中，a为常数。同样也可以合理地推测，平均株重w与D相关，表示为

其中，b为常数。整合方程25-8至25-10可得：

该式与方程25-5中的-3/2幕定律具有相同的结构，只是在这里，截距c由b（L/a）3/2所代替。

因此，可以很明显地看出，为什么自疏线的斜率通常被预期为-3/2。此外，如果方程25-9和方程25-10中的关系适用于所有的植物物种，且所有植物在单位土地面积上的叶面积（L）相同，那么，所有物种的常数c也大致相同。另一方面，如果某些物种的L并不恒定见方程25-8，或者方程25-9和方程25-10中的幂并非恰好是2或3，又或是这些方程中的常数（a和b）在种同存在差异或者根本不是常数。那么，自疏线的斜率将会偏离-3/2，并且斜率及截距会存在种间差异。根据几何学角度的讨论，我们就可以很容易地解释，为什么不同物种的自疏行为具有广泛的相似性，在仔细分析之后，也可以知道为什么单一的理想自疏线并不存在，且自疏线存在一定的种间差异。

与简单的几何学论点相反，在一个持续生长的植物同生群中，产量和密度之间的关系并不仅依赖于死亡个体的数量，它往往还依赖于存活个体的生长方式。我们已经知道，竞争常常是高度不对称的。如果同生群中死亡的主要是极小个体，那么密度（单位面积的个体数）会随着同生群的生长而迅速下降，于是斜率会变得更加平缓，特别是在自疏作用的早期。一个鼠耳芥（Arabidopsis thaliana）的相关研究可以证实这一观点，实验中，选用正常的拟南芥和其突变体，通过对两者自疏作用的比较发现，突变体对光敏色素A的过度表达极大地降低了它对阴影的耐受性，进而使得种内竞争变得更加不对称见图25-4a。

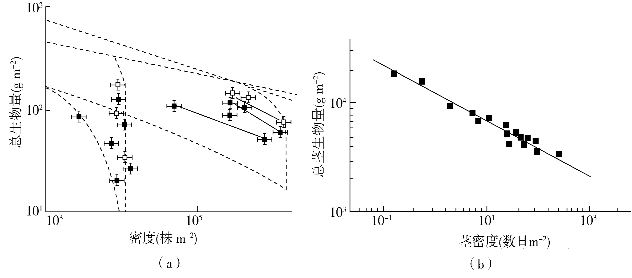
图25-4　（a）鼠耳芥（Arabidopsis thaliana）的两株野生型（□■）和一个光敏色素A过表达的突变体（●）在播种15、22、33天后（从下向上），总生物量与密度之间的关系。数据点表示平均值±SE，n＝3。在每种情况下，所有的生物性都以两种初始密度进行种植；黑色的回归实线表示较高初始密度下的情况。较陡的黑色虚线斜率为-1/2（标明符合-3/2自疏线），较平缓的线斜率为-1/3（标明符合-4/3自疏线）。图中分别表示了不对称（——）和对称（----）竞争的模型轨迹。突变体品系的自疏线更为平缓，标明不对称竞争作用更强。（b）日本北部赤松（Pinus desifloral）种群的物种界线（斜率＝-1．48）

此外，我们可以利用方程25-5～方程25-11来部分解释自疏线斜率与幂定律中-3/2间的差异。WswaAllen（1993）研究了山地假山毛榉（Notholagus slandr）和赤松（Pinus desifloral）个体生长的数据，并利用它们对这些方程中的一系列参数进行估算。例如，他们对方程25-9和方程25-10中指数的估算结果并非2和3，对于山毛桦来说是2．08和2．19，对于赤松来说则是1．63和2．41。这表明，自疏斜率在第一个例子中是-1．05，而在第一个例子中为-1．48，这与实际观斜率-1．06和-1．48非常一致（图25-4b）。此外，截距常数的估算值和实测值也非常相似。因此，这些结果表明，自疏线斜率也可以是除了-3/2之外的值，而且可以根据相关物种的详细生物学特性进行解释——然而即使物种的自疏斜率是-3/2，如红松，也是由其他原因导致的（是-2．41/1．63，而非真正的-3/2）。

（五）自疏界线的资源分配基础

基于几何学的讨论，以及在斜率估测时面临的统计学困难，越来越多的人意识到，斜率值可能非常多样化，而这将有助于形成对潜在趋势的另一种解释。West等（1997）提出了一个非常普遍的模型，该模型认为，生物（不只是植物）拥有精妙的结构设计，可以使获取的资源在生物体中进行最有效的分配。因此，Enquist等（1998）使用了该模型，并认为个体的资源利用率u应该与平均株重w相关，具体方程如下：

其中，a为常数。实际上，Enquist等（1998）还发现了这一关系的实验依据。

随后他们认为，植物已经进化出充分利用资源的能力，因此，如果S是单位面积的资源供应率，Nmax是植物的最大允许密度，那么，

或者，结合方程（25-12）可得出，

但是当植物的资源供应率达到稳态时，S应该是常数。因此，

其中，b也是常数。简言之，在这种情况下，种群界线的预期斜率应该是-4/3而不是-3/2。

Enquist及其同事认为，可获取的数据更支持种群界线的斜率是-4/3，而不是传统的-3/2。然而，这既不是之前数据调查的结果，也不是后续实验分析的结果。究其原因，一方面从几何学角度的讨论只关注了光吸收，因此，实验数据也很可能大多来自植物的地上部分（光合组织或支持组织）；Enquist等讨论的是更为普遍的资源获取，因此，他们所收集的数据至少部分是整株植株（叶子、茎和根）的质量。另一方面，Enquist等收集的数据关注大量物种的最大密度，其他研究则关注物种的自疏过程，而该过程通常发生于生物受到最大资源限制之前。因此，这两种方法可能并不矛盾。

（六）动物种群的自疏作用

无论是固着生活还是移动生活的动物，都应该具有自疏作用，在一个同生群内，个体的不断生长将导致不同个体之间发生竞争，并进而降低其自身的密度。对光的共同需求可以将所有的植物联系起来，然而，没有什么因素可以将动物联系起来，因此在动物中存在普遍自疏定律（self-thinning rule）的可能性很小。但是，密集的固着动物同植物一样，也需要在近乎恒定的区域内压缩体积。已有研究发现，贻贝的自疏线斜率为-1．4，藤壶的则为-1．6。此外，群居在智利海岸的被囊类动物Pyura praeputialis，其自疏线斜率仅为-1．2；但是相比植物，岩岸无脊椎动物的生存环境要更加“立体”，它们可以生活于一个被彻底占领区域中的多个平面（与植物恒定的叶面积指数相反），据此，对数据分析进行修正，新估算的斜率为-1．5见图25-5a。

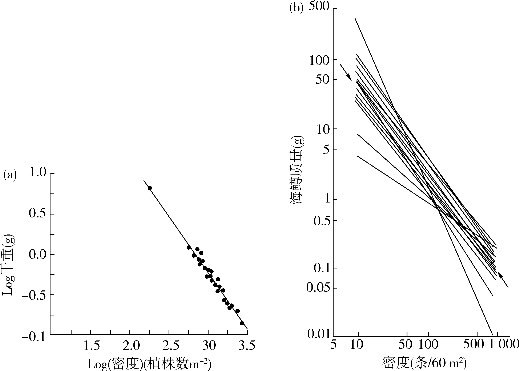
图25-5　被囊类群居动物Pyura praeputialis得自疏作用，修正后的密度考虑了“有效面积”，其中引入了被囊类动物定居的层数。估算的斜率为-1．49（95%CI：从-1．59到-1．39，P＜0．001）。（b）英国湖区溪流中23龄级褐鳟的动态自疏线，箭头表示平均回归线的位置（斜率为-1．35）。

对于非固着生活的动物，已有的研究表明，代谢率与个体大小之间的关系可以产生斜率为-4/3的自疏线。然而，这结论的普遍性可能比植物中的相应规律受到更多的质疑，考虑到资源供应的变化、潜在关系系数的变化，以及动物的自疏作用可能依赖于领域行为而不是简单的食物可利用性。尽管如此，仍有越来越多的研究证实了动物的自疏作用，特别是鱼类，但其机制尚不清楚见图25-5b。

植物中自疏作用模式与曾经想象的不是很一致，动物很可能比植物更加不符合常规的自疏定律。

三、种间竞争的Lotka-Volterra模型

Lotka-Volterra模型是生物学领域较为经典的模型，由美国生物学家、数学家A．Lokta于1925年首先独立提出，适用于两个互相作用种群的动力学系统。后来，意大利著名数学家Volterra在此模型的基础上改进形成了两种群捕食及竞争模型的Lotka-Volterra模型。此后，很多生物学学者和数学学者对Lotka-Volterra模型进行研究。

Loka-Volterra的种间竞争模型是逻辑斯谛模型的延伸。设N1和N2分别为两物种的种群数量，K1、K2、r1和r2分别为这两物种种群的环境容纳量和种群增长率。按逻辑斯谛模型(www.chuimin.cn)

如前所述，（1-N/K）项可理解为尚未利用的“剩余空间”项，而N/K是“已利用空间项”。

当两物种竞争或共同利用空间时，已利用空间项除N1外还要加上N2，即：

其中α为竞争系数，它表示每个N2个体所占的空间相当于α个N1个体。举例说，N2个体大，消耗的食物相当于10个N1个体，则α为10。显然，竞争系数α可以表示每个N2对于N1所产生的竞争抑制效应。同样，对于物种2：

β为物种1对物种2的竞争系数。方程式（1）和（2）即为Lotka-Volterra的种间竞争模型。

两物种的竞争结局从理论上讲可有以下3种：种1胜而种2被排除；种2胜而种1被排除；两种共存。Lotka-Volterra种间竞争模型的行为可说明获得各种竞争结局的条件。图25-6a和6b分别表示物种1与2处于平衡状态即dN1/dt＝0、dN2/dt＝0时的条件。在（a）图中，最极端的两种平衡是：（1）全部空间被N1所占，即N1＝K1，N2＝0。（2）全部空间被N2所占，即N1＝0，N2＝K1/a。连接这两个端点，即代表了所有的平衡条件。在对角线以下和以左N1增长，以上和以右N1下降。同样（b）图中对角线以下和以左N2增长，以上和以右N2下降。将（a）和（b）图相互叠合起来，就可得到下列4种不同的结局，其结果取决于K1、K2、K1/α和K2/β的相对大小见图25-7。

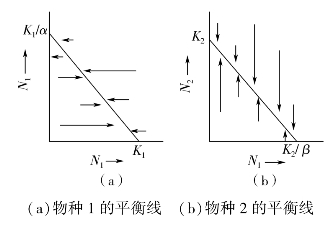
图25-6　Lotka-Volterra竞争方程所产生的物种1和物种2的平衡线（仿Begon等，1986）

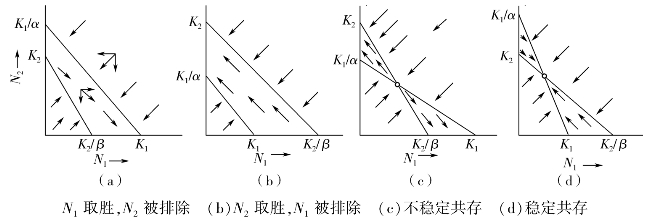
图25-7　Lotka-Volterra竞争模型的行为所产生的4种可能结局（仿Begon等，1986）

（a）当K1＞K2β，k2＜K1/α时，N1取胜，N2被排除。直观地说，在K2-K2β线右面N2已超过环境容纳量而停止生长，而N1能继续生长，因此结果是N1取胜。

（b）当K2＞K1/α，K1＜K2/β时情况与上相反，N2取胜，N1被排除。

（c）当K1＞K2β，K2＞K1/α时，两条对角线相交，出现平衡点，但这样的平衡是不稳定的。

（d）当K1＜K2/β，k2＜K1/α时，两条对角线相交，出现平衡点，平衡点是稳定的。

1/K1和1/K2两个值，可分别作为种1和种2的种内竞争强度指标。因为在一个空间中，如果能“装下”更多的同种个体（即K1值越大），则其种内竞争就会相对越小（即1/K1值越小）。同样道理，β/K2值可作为物种1对物种2的种间竞争强度，α/K1值可作为物种2对物种1的种间竞争强度。这样，竞争的结局取决于种间竞争和种内竞争的相对大小。如果某物种的种间竞争强度大，而种内竞争强度小，则该物种取胜，反之被排除。将上面（a）和（b）两种情况分别取倒数可知（a）情况下A种内竞争强度小，种间竞争强度大，而N2相反，所以N1取胜，N2被排除。在（c）情况下，取倒数得：1/K1＜β/K2，1/K2＜α/K1，两物种都是种内竞争强度小，种间竞争强度大，都有可能取胜，因而出现不稳定的平衡。情况（d）与（c）相反，两物种都是种内竞争强度大，种间竞争强度小，彼此都不能排挤掉对方，从而出现稳定的平衡，即共存的局面。

（一）Lotka-Volterra捕食者—猎物模型

Lotka-Volterra捕食者-猎物模型是一个简单然而有价值的模型。该模型做了以下简化假设：1．相互关系中仅有一种捕食者与一种猎物。2．如果捕食者数量下降到某一阈值以下，物种数量就上升而捕食者数量如果增多，猎物种数量就下降，反之，如果猎物数量上升到某值，捕食者数量就增多、而猎物种数量如果很少，捕食者数量就下降。3．猎物种群在没有捕食者存在的情况下按指数增长，捕食者种群在没有猎物的条件下按指数减少。即：dN/dt＝r1N，DP/dt＝-r2P，其中N和P分别为猜物和捕食者密度，r1为猎物种群增长率，-r2为捕食者的死亡率，t为时间。

当二者共存于一个有限空间内，猎物种群增长因捕食而降低，其降低程度决定于：1．N和P密度，因二者决定捕食者与猎物的相遇频度。2．捕食者发现和进攻猎物的效率e，即平均每一捕食者捕杀猎物的常数。因此猎物方程为，

同样，捕食者种群将依赖于猎物而增长，设θ为捕食者利用猎物而转变为更多捕食者的捕食常数，则捕食者方程为

方程25-19和25-20即为Loka-Volterra捕食者-猎物模型。图25-8a表示猎物种群的零生长等斜线，捕食者的临界密度。猎物的零增长，即dN/dt＝0时，r1N＝ePN或P＝r1/e。因为r1和e均是常数，所以猎物零生长线是一条直线。当捕食者种群超过该密度，则猎物种群由被捕食导致的死亡率超过出生率，N减少，反之N增加。同样，图25-8b表示捕食者种群的零生长等斜线，这时N＝r2/θ，是临界猎物密度。当猎物种群低于该密度，捕食者种群会因为饥饿而数量下降，反之，数量上升。

将以上两条等斜线与猎物和捕食者的数量变化结合起来，就得到猎物和捕食者共同的瞬时数量变化见图25-8c和8d。几乎不管捕食者和猎物的起始数量如何（只要两者数量大于零），就会出现一个循环模式：猎物数量上升，紧跟着捕食者数量也上升，而后者数量的上升会减少前者数量，最后导致后者数量也下降。这样，猎物数量又开始上升，循环再次开始。注意图25-8所示的循环模式代表单一结果，不同的起始数量会导致不同量级的循环。另外，模型预言的周期性振荡对外界干扰很敏感，外界环境改变会导致循环量级的改变。

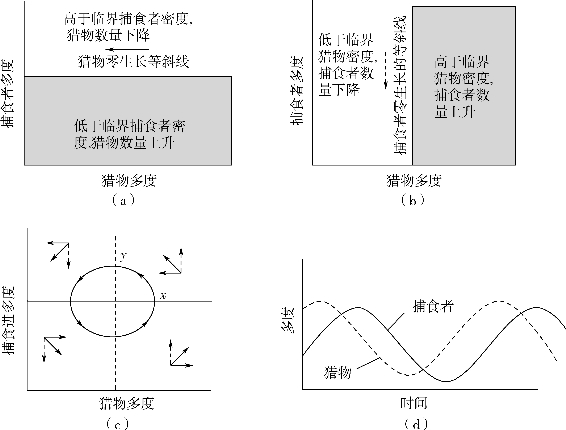
图25-8　Lotka-Volterra捕食者—猎物模型（仿Mackenzic等，2000）

注：（a）猎物零生长等斜线　（b）捕食者零生长等斜线　（c）结合两等斜线得出捕食者与猎物共同瞬时变化（实线箭头，猎物数量变化；虚线箭头，捕食者数量变化）。最大猎物数量发生在y　（d）（c）中所示捕食者与猎物数量对时间（为横轴）作图的双循环

（二）数学模型

1．Lotka和Volterra分别在研究化学反应和解释Finme港鱼群变化规律时，将Finme港中的鱼分成两类，即食用鱼与掠肉鱼，建立经典的食饵-捕食生物模型：

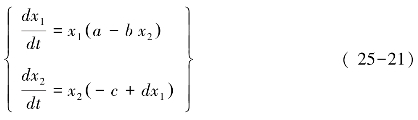
式中，x1为食饵的密度；x2为捕食者的密度；a、b、c、d为常数，可正，可负或为0。

考虑更一般的情况，两个种群的生长中的相互关系可用Volterra模型表示：

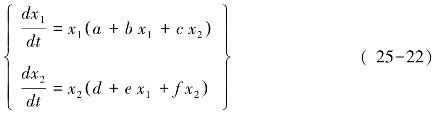
系数a、b、c、d、e、f为常数，可正，可负或为0，视两种群的相互关系而定，一般分竞争、共生、食饵-捕食等类型。就一个种群来说，如x2＝0或x1＝0，种群内部存在密度制约关系时即为一维的Logistic模型。

在模型（1）（即式25-19）的基础上，引入一类新的物种与捕食者形成竞争关系的物种，但不与食饵以及捕食者形成捕食关系，此物种与食饵及捕食者物种共同成长在密度一定的空间领域中，根据三种物种之间的密度关系建立新的微分代数Lotka-Volterra食饵-捕食生物模型：

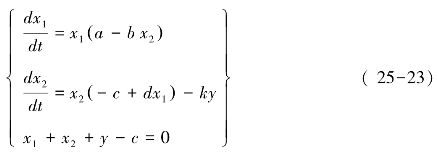
式中，y为竞争种群的密度；k为随着y的增多而x2减少的比率系数；a、b、c、d均为正数。

四、群落中性理论模型

（一）理论模型概述

生物多样性的分布格局和维持机制一直是群落生态学研究的核心问题，其中的关键是物种的共存机制。长期以来，生态位分化的思想在这一研究领域占据着主导地位。然而这一理论在解释热带雨林很高的物种多样性时遇到了困难。而以Hubbell为代表提出的群落中性漂变理论则假定在同一营养级物种构成的群落中不同物种的不同个体在生态学上可看成是完全等同的；物种的多度随机游走，群落中的物种数取决于物种灭绝和物种迁入/新物种形成之间的动态平衡。在这一假定之下，该理论预言了两种统计分布。一种是集合群落在点突变形成新物种的模式下其各个物种相对多度服从对数级数分布，而受扩散限制的局域群落以及按照随机分裂为新物种模式形成的集合群落则服从零和多项式分布。与生态位理论相反，中性理论不以种间生态位差异作为研究群落结构的出发点，而是以物种间在个体水平上的对等性作为前提。该理论第一次从基本生态学过程（出生、死亡、迁移、物种分化）出发，给出了群落物种多度分布的机理性解释，同时其预测的物种多度分布格局在实际群落中也得到了广泛的印证。因此，中性理论自诞生以来便在生态学界引发了极大的反响，也包括一些反对的声音。本节将系统地介绍中性理论的假设、模型和预测，最新的理论和实验研究进展，以及相应的检验工作。

（二）物种多度分布模式和群落中性理论

群落生态学的一个重要内容就是探讨群落内物种相对多度的模式，并给出机理解释。早在20世纪40年代，统计模型就被用来描述观测到的物种多度分布模式。Fisher等把多度曲线F（n）定义为在一个包含J个个体的样本中个体数为n的物种数，可用下面的公式来计算：

其中，a＞0，0＜x＜1是常数。由Taylor展开式可知：

由公式25-24定义的Fα（n）恰好正比于上述对数展开中的各项，故称此分布为对数级数分布或对数分布（Logarithmic distribution）。α即著名的Fisher-α。

因为

则，并且可得

这里的多样性指数α曾被用来拟合个体数量大的昆虫和动物的数据，但是它的理论基础并不清楚。而且当应用于热带雨林时，人们发现它经常低估了物种数。

除了Fisher的物种多度模型之外，Preston（1948）提出了另外一个著名模型。他把物种的个体数转换成以2为底的对数，并进行合并，即按照物种的个体数分别为1、2～3、4～7、8～15等进行分组。在这种模式下，他认为观测到的数据符合钟形曲线，物种数-多度的最佳拟合分布是对数正态分布，而不是Fisher所说的对数级数分布。实际观测到的数据有很多符合对数正态分布（Tokeshi 1990），但也并不都是如此。以BCI的数据为例，对数正态分布预言了太多非常丰富的物种以及太少的稀有物种。

Fisher和Preston等的模型并不依赖于统计学过程。真正把统计理论和统计种群模型联系起来的是种群遗传学中Karlin和McGregor（1967）提出的中性模型。虽然这一模型的背景是种群遗传学，但只需用“物种”“物种分化和迁移”“群落”分别代替模型中的“基因型”“突变”和“种群”，就很容易将它平移到生态学中来。在这个模型中，群落的大小是固定的，即包含J个个体，在每一代，新物种形成的速率为ν。因此，新物种通过迁移或物种分化以速率为ν的泊松过程进入系统。群落中共有S个物种，第i物种的多度ni在单位时间内只能增加或减少1个单位。Karlin和McGregor（1967）研究了F（n），即当ni＝n时，种i的期望多度也就是群落生态学中的物种数-多度分布。假定有很多明显不同的物种，并且所有的物种都是小种群，则物种数-多度服从对数级数分布：

其中λ和μ分别是单位出生率和死亡率与种群大小的比值。和公式25-24相比较，VJ相当于Fisher-α，而λ/μ相当于公式中的x。

（三）中性理论的假设

Hubbell（1979，2001）发展了岛屿-生物地理学中MacArthur和Wilson（1963，1967）的扩散装配理论，提出建立在个体水平上的群落生态学中性理论，认为生态学上相同的物种可以实现共存，物种多度的变化是随机的，而非确定性的；共存的物种数量取决于物种分化（或迁入）和随机灭绝之间的平衡群落内物种的相对多度随时间表现为随机振荡的波动。之所以被称为中性理论，是因为这一理论假定群落中所有的个体在生态学上都是完全等同的（或者对称的）：具有相同的出生率、死亡率、迁移率以及新物种形成的概率。

群落中性理论的两个基本假设是：1．群落内生物个体总的数量固定，某一物种多度的上升必然伴随着其他物种个体数量同等程度的减少；2．所有物种的个体都具有完全相同的出生率、死亡率和扩散率。

假定局域群落始终是充满的，群落中所有的个体在生态学上是相同的（或者对称的），即它们具有相同的出生、死亡、迁移的概率。并假定单位时间内死亡的个体数D＝1，即单位时间内有且只有一次死亡和出生事件发生。

在大小为J的局域群落中，种i增加一个个体，种j减少一个个体的概率为：

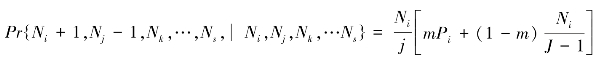
相对物种多度不变的概率为：

其中m是单位迁移率，Pi是种i在集合群落中的相对多度。这个转移概率矩阵的特征向量给出了局域群落中各种可能的相对多度组合（假设共有C个）的可能性，记第k个相对多度组合出现的可能性为φ（k），则大小为J的局域群落中按多度排序后物种的期望多度为：

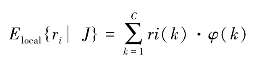
在这些假定条件下，它预测局域群落内物种相对多度的分布符合“零和多项式分布”（Zero-summultinomial distribution），而非先前普遍接受的“对数正态分布”。与对数正态分布相比，零和多项式分布曲线在稀少物种一侧的尾部较长，其长度取决于局域群落的大小和个体扩散速率见图25-9。在解释热带雨林树种的相对多度分布以及种数-面积关系等方面，该理论获得了巨大的成功，尽管在绝大多数情况下不同物种不可能有完全相同的生育率、死亡率和扩散速率。事实上，Hubbell本人也承认他所研究的雨林树种在生长速率和耐阴能力等方面存在着显著差异，但是他认为这些差异对群落结构的形成并不重要，而发生在个体水平上的统计随机性将成为最主要的决定因素。

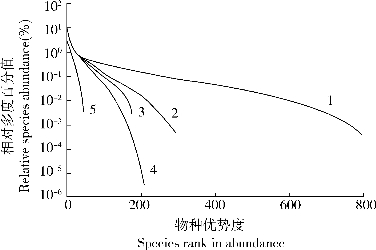
图25-9　不同群落中的物种相对多度分布模式

注：群落中的物种按照其相对多度从大（左）到小（右）排列。Y轴采用对数刻度，表示物种相对多度的百分值　1．亚马逊潮湿的热带雨林　2．哥斯达黎加的热带干燥落叶林　3．北太平洋旋涡的海洋桡脚类浮游生物群落　4．英国的陆地鸟类群落　5．巴拿马热带蝙蝠群落（引自Hubbell，2001）

五、Habbell生物多样性和生物地理学中性理论

Habbell（2002）已经发展了具有挑战性的新的中性模型，扩展了MacArthur和Wilson岛屿生物地理学平衡理论来说明区域及局城生物多性格局，这一方法将复合群落定义为进化过程中出现的相似营养级的生物所组成的大尺度聚集。每个复合群落由一组局部群落组成，Hubbell模型假设群落总是被个体饱和，N和面积A有确定关系。直到N因个体死亡而减小时，新个体才出生或迁移加入。每一个体在局部群落的相对多度与它在复合群群落的多度有关，复合群落的多度依次有五种形成而形成。Hubbell理论可以用一个单-无量纲的生物多样性指数θ来概括，θ等于物种形成速率的2倍乘以复合群落大小。这个生物多样性指数可以预测物种相对多度。例如，如果保持复合群落大小（N）为常数，随着物种形成速率增加，会出现许多稀有种，或者物种形成速率V可能不变，探究复合群落大小变化的结果。在复合种群中，不同物种形成模型导致复合群落不同的物种多度分布。如果点突变，即新物种以单一个体出现成为新物种形成的主要形式，那么物种多度分布就服从对数级数分布，相反，如果物种形成时随机裂变，即产生多度大致相同的姐妹种，那么就会产生物种多度的零和多项式分布。

如果迁入不受限制，局部群落物种多度格局将会与集合群落一样（尽管物种丰富度会随者局部群落的空间大小降低而减少因此，它能维持的个体数量也减少），因此它就遵循对数级数或者零和多项式分布，这取决于物种形成方式。或者如果迁入受到严格限制，可能有扩散障碍，那么多度会类似于对数正态分布。这种情况可由N和A的关系来解释，物种消失必须通过增加现有种的多度来补偿，因为有几个移殖种能成为群落新种，但这往往非常稀少。如果迁入率适中，物种多度分布就会左偏，这种格局常在自然集聚存，受扩散限制，局部群落物种多度分布服从零和多项式分布，与复合群落的分布形式无关。

Hubell模型因其解释大范围的经验物种多度分布的能力而出名，然而Hubbll定义的中性假设“在一定营养级物种构成的群落中，不同物种的不同个体在生态学上是等同的”，与许多生态学家熟悉的生态系统功能多样性的本质相反，群落优势种的特性完全是偶然似乎不太可能，Gaston和Blackburn也同意集聚被它们维持的许多个体数所饱和的假设。Magurran和Henderson（2003）已独立表明扩散限制能解释局部群落物种多度分布的特有左偏分布。与Hubbell方法相比，假设生物相互作用起了重要作用。

Hubbell模型已激起了人们很大兴趣，并且无疑还会激发许多新研究，困难的是需要对经验数据进行模拟来估计基础生物多样性数量和扩散率。Hubbell（2001）提供了计算复合群落期望相对多度分布的方法，但假设物种形成为点突变。