通过排序分析，既可以认识群落格局，也可以将排序轴跟我们已知的环境条件联系起来，看是否代表某一环境梯度。包括约束性排序和非约束性排序。5．非约束性排序：寻求潜在的或在间接的环境梯度来解释物种数据的变化。图16-1物种响应环境梯度模型但对于单峰响应模型，估计物种在环境梯度上最适值最简单的方法就是通过基于所有包含该物种的n个样方中环境因子值的加权平均得到。......
2023-11-17
生态数据分析与建模：排序图解读及应用
【摘要】：也可以用图16-6的形象方法解读，将变量B反向延长，物种1和物种分别投影于其上，可以很清楚地看出物种2的投影与B同向，代表正相关；同理，物种1为负相关。图16-12基于RDA双序图上分析物种沿海拔梯度分布情况2．基于单峰模型排序图的解读。
CANOCO相对于R、Primer等大致同功能的统计分析软件来说操作过程容易上手，界面比较直观，不需要记忆复杂的语言代码，做出来的排序图质量也是不用质疑。考虑到CanoDraw出图的多样性（不同设置生成不同排序图），这里主要介绍排序图的解读方法。
一、基于线性模型排序图的解读
出于介绍的简洁性，采用的是分解介绍法，实际过程中可能遇到上述某些图呈现在一个排序图中情况，解读方法类似。
1．物种和样方间关系。
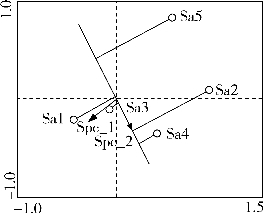
图16-3
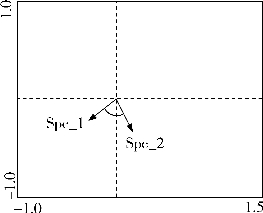
图16-4
如图16-3，带箭头射线代表物种，空心圆点代表样方。将物种2（spc＿2）的射线延长，五个样方均垂直投影到该射线上，以投影点到物种实心箭头处相对距离为标准，沿着箭头方向为增大，反之为减小，作用是用来说明相应样方中物种2的多度值大小；样方3的投影点在原点附近，可以认为该样方中物种2多度值大致等于其平均值；该图中各样方中物种2多度值排序为：Sa4＞Sa2＞Sa3＞Sa1＞Sa5。物种1和各样方关系以相同方法分析。
2．物种和物种间关系。
如图16-4两物种射线之间夹角代表其相关性，具体地说应该是夹角的余弦值在数值上等于两者的相关系数。图中两物种的夹角接近于直角，所以认为两者相关性较低。
如图16-5实心箭头代表物种，空心箭头代表环境变量。以环境变量B和两物种之间的关系为例进行阐述：B和物种1、物种2夹角分别为a1，a2，前者是个钝角，后者是个锐角，相应的余弦值代表了之间的相关性，很明显，环境变量B和物种2之间呈现较好正相关，与物种1呈现负相关。也可以用图16-6的形象方法解读，将变量B反向延长，物种1和物种分别投影于其上，可以很清楚地看出物种2的投影与B同向，代表正相关；同理，物种1为负相关。
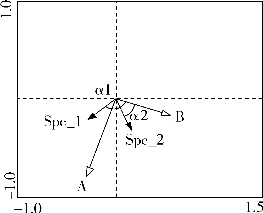
图16-5
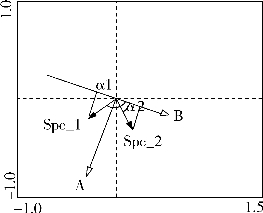
图16-6
如图16-7实心正方形代表不同的形式变量值或者说不同的类别，射线箭头代表物种。延长物种射线，将形式变量投影于物种线上，投影点距离物种箭头近者，代表该类别中样本所含的该物种多度平均值较高。在此图中，类别n＿II中样方所含的物种2多度相对于其他两个类别高。同理，物种1和形式变量关系也可以采用相同方法分析。
4．样方和样方之间关系。
如图16-8圆点代表样方。如果要解读某一样方和其他样方之间的关系，可以如图用直线将该样方和其他样方连接起来，之间的线段长度便是样方之间的欧几里德距离，长度越短代表两者之间的差异性越小，反之越大。图中其他四个样方和Sa5差异性大小依次为：Sa1＞Sa4＞Sa3＞Sa2。
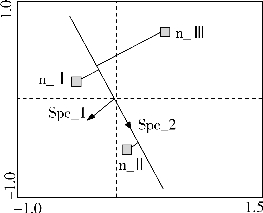
图16-7
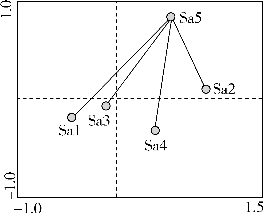
图16-8
5．样方和环境变量间关系。
如图16-9将变量射线延长，样方垂直投影于射线上，沿着变量箭头方向环境变量值增大。图中样方Sa3和Sa4所对应的环境变量A值近似相等，所有样方中变量A值大小排序为：Sa1＞Sa4＾Sa3＞Sa2＞Sa5。变量B和样方间关系也采用类型方法分析，不再赘述。
6．样方和形式变量间关系。
如图16-10想知道某一样方和形式变量之间关系可将该样方和形式变量用线段连接，线段长度代表了该样方属于某一形式变量类别的概率，距离越短，概率越大；反之，越小。如图，Sa1属于不同形式变量类别概率为：n＿I＞n—II＞n—III。其他样方和形式变量类别之间所属概率也可以按照此方法进行分析。
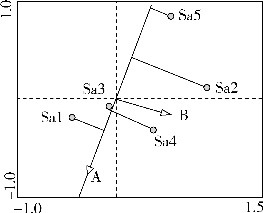
图16-9
图16-10
7．形式变量和形式变量间关系。
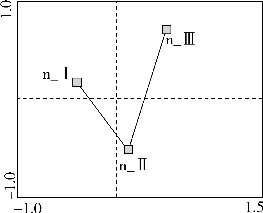
图16-11
如图16-11不同形式变量之间连线的长度代表欧几里得距离，距离越短，形式变量所代表类别间样本间差异性越小；反之，越大。
二、PCA排序图的解读
以不同海拔高度6种典型植被带土壤微生物PLFAs指纹图谱进行主成分分析为例，通过方差分解主成分提取分析见表16-1，总共提取出4个主成分因子，前三个主成分累积贡献率达到85．484%，大于85%。因此，第一主成分、第二主成分和第三主成分为主要解释的主成分。(www.chuimin.cn)
表16-1 方差分解主成分提取分析
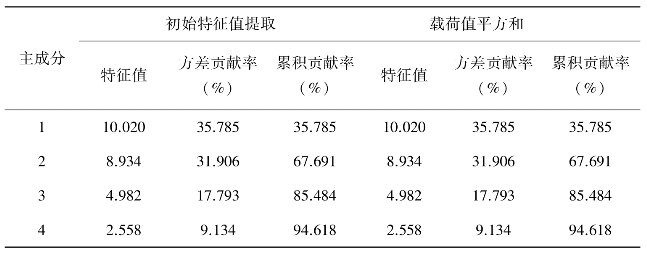
第一主成分能解释35．79%的变异，第二主成分能够解释31．91%的变异，第三主成分能够解释17．79%的变异，各植被带土壤之间的差异主要是由第一主成分和第二主成分引起的。因子载荷矩阵分析结果显示见表16-2，第一主成分主要反映了细菌和真菌的生物量信息，第二主成分主要反映了细菌生物量的信息。综合以上分析，说明各植被带土壤中细菌与真菌含量差异较大。由此可以看出，第一主成分所包含的脂肪酸类型是本研究试验土壤的主要PLFAs类型。
表16-2 磷脂脂肪酸甲脂主成分分析因子载荷矩阵
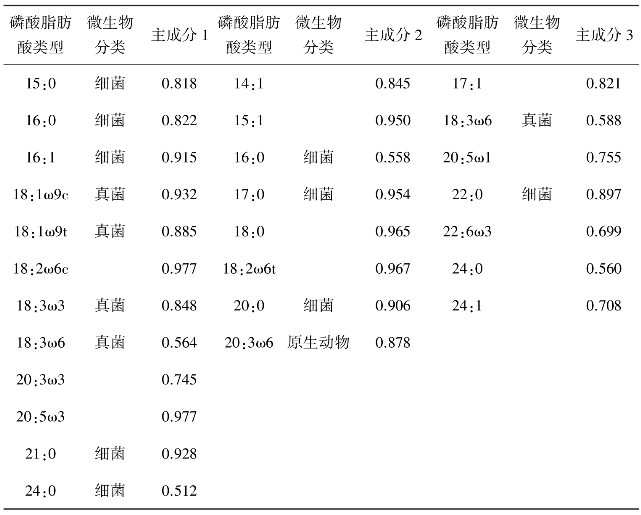
三、RDA排序图的解读
冗余分析的最大优势在于能独立保持各个变量对生物群落变化的贡献率，并从统计学角度评价一个或一组变量与另一组多变量数据间的关系。
1．基于线性模型排序图的解读。
图16-12是专门分析单一环境变量Altitude对物种群落影响的实例。第一轴（水平轴）代表能被环境变量Altitude所解释的物种多度变化值，属于约束轴；第二轴代表不能被其解释的变化值。从图中可以看出随着Altitude变量的增加物种多度是减小的，并且只给出了能被改变量很好解释的物种。其他要素间关系分析可以根据个人目的参照前述内容。
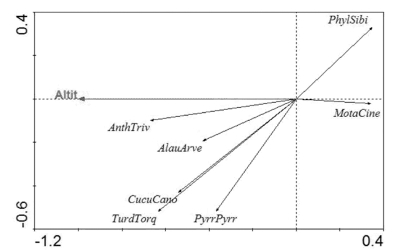
图16-12 基于RDA双序图上分析物种沿海拔梯度分布情况
2．基于单峰模型排序图的解读。
同线性模型排序图类似，单峰模型排序也有自己蕴含的解读信息。
（1）物种和样方间关系如图16-13可以发现在基于单峰模型生成的排序图中，代表物种的不再是箭头而是空心三角形，样方依然是实心圆点。用线段连接目标物种与样方，线段的长短代表了相应样方中目标物种的相对多度值高低，越短多度值越大，反之越小。图中各样方所含Spc＿2相对多度值高低顺序为：Sa4＞Sa3＞Sa1＞Sa2＞Sa5。物种1分析方法类似。
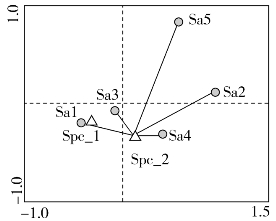
图16-13
图16-14
（2）物种和物种间关系如图16-14物种之间的线段距离被称为物种分布的卡方距离，其长短代表了物种间的亲疏关系，越长代表分布差异性越大，反之越小。
（3）物种和环境变量间关系如图16-15物种垂直投影于环境变量延长线上，物种2距离变量箭头的相对位置较物种1近，可以认为物种2在环境变量B较大时具有最适值，而物种1的最适值相对较低。
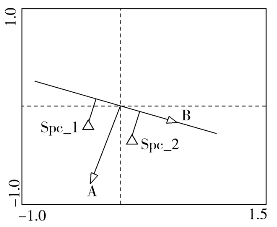
图16-15
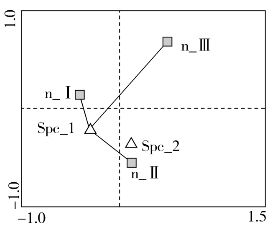
图16-16
（4）物种和形式变量间关系如图16-16物种和不同形式变量类别之间的距离代表了该物种在相应类别中的相对出现频率平均值大小，距离越大该值小，反之越大。图中各形式变量类别中物种1出现频率平均值大小依次为：n＿I＞n＿II＞n＿III。物种2分析方法类似。
（5）样本和环境变量间关系样本和环境变量间关系分析方法与上述的物种和环境变量解读方法类似。如图16-17，将样方投影于环境变量延长线上，投影点的相对位置代表了样方中环境变量值的大小。图中两样方中环境变量B大小关系为：Spc2＞Spc1。
图16-17
（6）样本和形式变量间关系与基于线性模型排序图解读方法一致，不再赘述。
（7）形式变量和环境变量间关系与基于线性模型排序图解读方式一致，不再赘述。
（8）形式变量和形式变量间关系此关系解读与样本和样本间关系解读一样，相对较复杂，不同形式变量类别之间的距离虽然类似于样本间差异性，但涉及距离种类较多，比如平均卡方距离、Turnover距离，同时也和排列尺度类别不同有关，具体内容可参考相关教材。
四、CCA排序图解读
箭头表示环境因子，箭头连线的长度代表着相应环境因子与研究对象分析相关程度的大小，越长代表其对所研究对象的分布影响越大；箭头连线与排序轴夹角余弦值代表其与排序轴的相关性大小，具体的分析方法可以参考上述基于单峰模型的排序图解读。
五、线性模型和单峰模型排序图解读差异
基于线性模型和单峰模型生成的排序图解读差异主要体现的两点。
1．物种对构建的梯度（或者说排序轴）响应不同。从本章前面的介绍可以发现，线性排序图很多时候都需要延长向量线，并且只在两个方向上探讨关系，即与向量同向或反向；单峰模型则不同，物种在每个排序轴上都有自己最适的多度值，并且物种多度值由此向四周任何方向的变化都是对称且逐步减小的。
2．另一个重要差异是样方之间的差异性问题。线性模型排序图中样方间差异性是基于欧几里得距离标准，而单峰模型排序图中则是基于卡方距离标准。如果不同样方中物种相对多度相同，比如含有相同三物种的两样本，各自物种数分别为1、2、1；10，20、10，在单峰模型排序方法中会认为两样本一致，没有差异性。与此同时，在单峰模型中不同物种分布间的差异性也是用卡方距离标准来衡量的。
有关生态数据分析与建模的文章
- 详细阅读
-
生态数据分析与建模：灵敏度分析及应用详细阅读
灵敏度分析试图测量模型的一些参数、强制函数、状态变量初始值，或子模型对最重要状态变量的灵敏度。因此，对于参数P的灵敏度定义如下：S＝［x/x］/［P/P］式中：x代表所考虑的状态变量。通常需要在两个或多个水平上发现参数变化的灵敏度，因为参数和状态变量之间的关系很少是线性的。如果发现所观察的状态变量对某个子模型很灵敏，应该考虑哪几个别的子模型可以替换使用，这些子模型应在野外或实验室做进一步的具体检验。......
2023-11-17
-
CANOCO排序方法-生态数据分析详细阅读
3．一个数据集被另一个数据集解释后，再被第三个数据解释——偏典范排序。图16-1CANOCO分析数据的一般流程1．排序模型的决定。表16-1基本排序方法和排序模型对照表3．CanoDraw作图。......
2023-11-17
-
《生态数据分析与建模》：土壤数据的重要性及分详细阅读
土壤无论对植物来说还是对土壤动物来说都是重要的生态因子。由于在土壤中运动要比大气中和水中困难得多，所以除了少数动物能在土壤中掘穴居住外，大多数土壤动物都只能利用枯枝落叶层中的孔隙和土壤颗粒间的空隙作为自己的生存空间。因此，土壤数据包括野外调查数据，比如枯枝落叶层的厚度、土壤类型、土壤厚度和剖面特征、土壤温度等。室内测定数据包括土壤结构、土壤容重、土壤水分、土壤物理特性及化学特性。......
2023-11-17
-
生态数据分析与建模：数据标准化方法及实例详细阅读
为了消除量纲影响和变量自身变异大小和数值大小的影响，故将数据标准化。经过标准差标准化后，数据都是没有单位的纯数量。尽管如此，它还是当前用得最多的数据标准化方法，也是SPSS中最为常用的标准化方法。即第三步，再对变量进行标准差标准化，即将某变量中的观察值减去该变量的平均数，然后除以该变量的标准差。表13-7长江17个观测点的水质分析表数据转换步骤如下：1．数据的标准化处理。......
2023-11-17
-
生态数据分析与建模：对数函数曲线及其应用详细阅读
如果两个变量的成对观测值在坐标系中的散点图分布趋势类似于对数函数曲线见图8-3，可配合对数曲线方程＝a＋blg x。图8-3对数曲线＝a＋blg x的图像［例10］在大棚育苗中，塑料薄膜苗床内空气最高温度和室外空气最高温度资料如表8-1所示。表8-1苗床内最高温度（y，℃）与空气最高温度（x，℃）的关系图8-4苗床内最高气温y与空气最高气温x的关系图8-5例18资料x′与y之间的直线关系2．配合对数函数方程。......
2023-11-17
-
生态数据分析与建模：直线回归分析的计算详细阅读
直线回归是回归分析中最简单的一种，又称为简单回归。（一）直线回归方程散点图上呈现直线趋势的两个变数，自变量x的每一个取值都有y的一个分布与之对应。试计算其直线回归方程。为简化手续，可从以下恒等式得出：（五）直线回归的数学模型和基本假定回归分析的依据是直线回归模型。......
2023-11-17
-
生态数据分析与建模：概率分布及正态分布详细阅读
试验结果只能是“非此即彼”构成对立事件，将这种事件构成的总体称为二项总体，其概率分布称为二项分布。显然，二项分布是一种离散型随机变量的概率分布。此外，还有不少随机变量的概率分布在一定条件下以正态分布为其极限分布。关于正态分布的概率计算，我们先从标准正态分布着手。......
2023-11-17
相关推荐