在项目结束后，华智按照要求对各项成本分别进行测量。在项目实施过程中，项目规模数据可能会随着项目目标的变化而发生变化，因此需要在项目不同阶段、各里程碑对项目规模数据进行重新测量、采集。在项目组完成直接成本的估算后，项目采集小组将数据采集至数据采集表中。华智财务部门在统计间接人力成本时，会直接计算、采集以上非项目组人员的人力资源费用，以上数据直接可以从组织的财务系统中采集获得。......
2023-11-19
生态数据采集整理方法
【摘要】：3．数据整理的方法。其次，对进行方差分析的数据，应检查是否符合方差分析的基本前提或基本假定。如果试验资料不具备这一性质，变量的总变异依据原因的分解将失去根据，方差分析不能正确进行。
一、数据采集
在生态学研究中，水、土、气、生数据采集是科学研究的基础。随着国家对生态文明建设和环境保护工作的重视，各级农业、林业、水利、国土、环保、气象等部门，充分利用遥感、物联网、互联网等信息技术手段，系统收集水、土、气、生等生态要素的数据资料，为构建生态大数据提供基础数据，探索建立多部门协同合作的生态环境数据共建共享机制。
陆地生态系统和水域生态系统的观测指标及其规范有差别。陆地生态系统主要包括农田、森林、草地、荒漠、沼泽等生态系统类型，其观测指标体系：观测场地的定义和设置方法；样品采集、处理和保存方法；野外观测方法和室内分析方法；数据管理和质量控制。水域生态系统观测规范包括：观测的基本原则和采样方法，水域自然地理与周边社会经济调查；湖泊和海湾生态系统基本要素的监测；数据管理和质量控制。
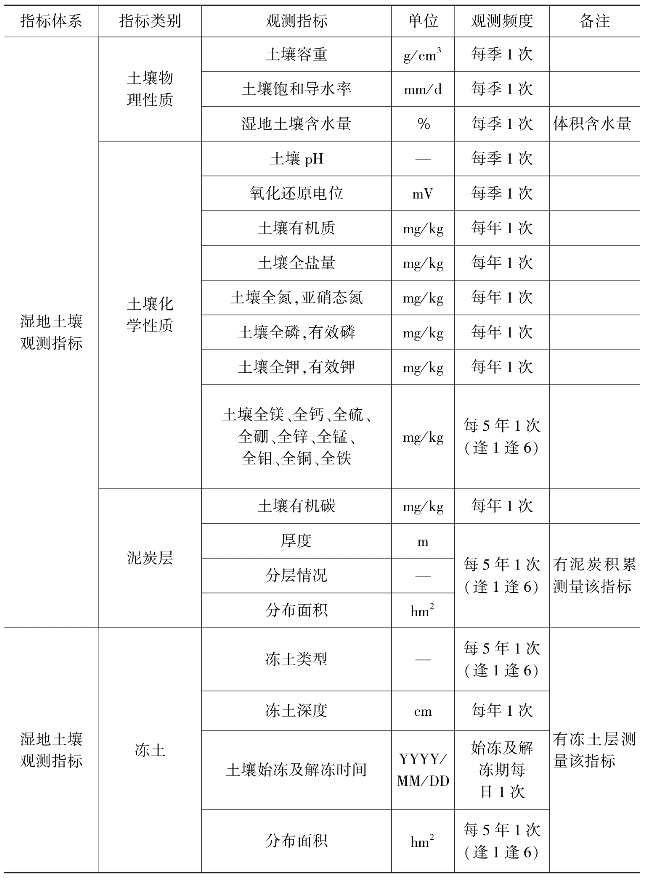
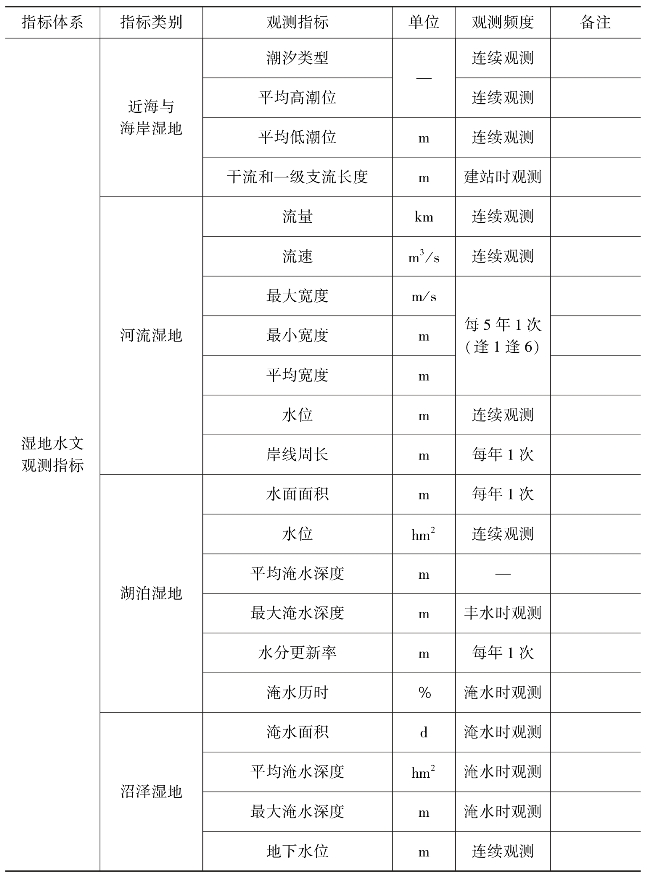
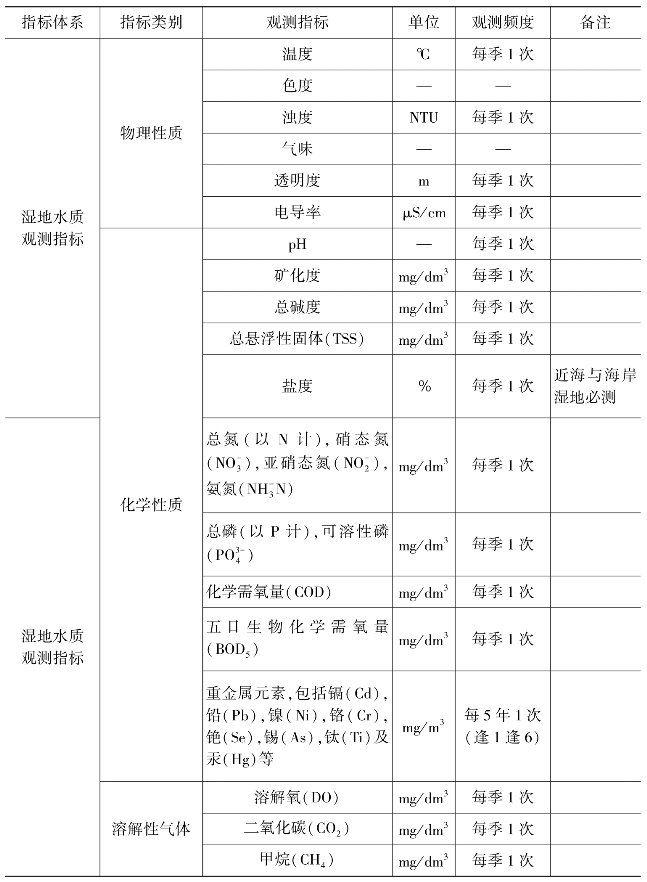
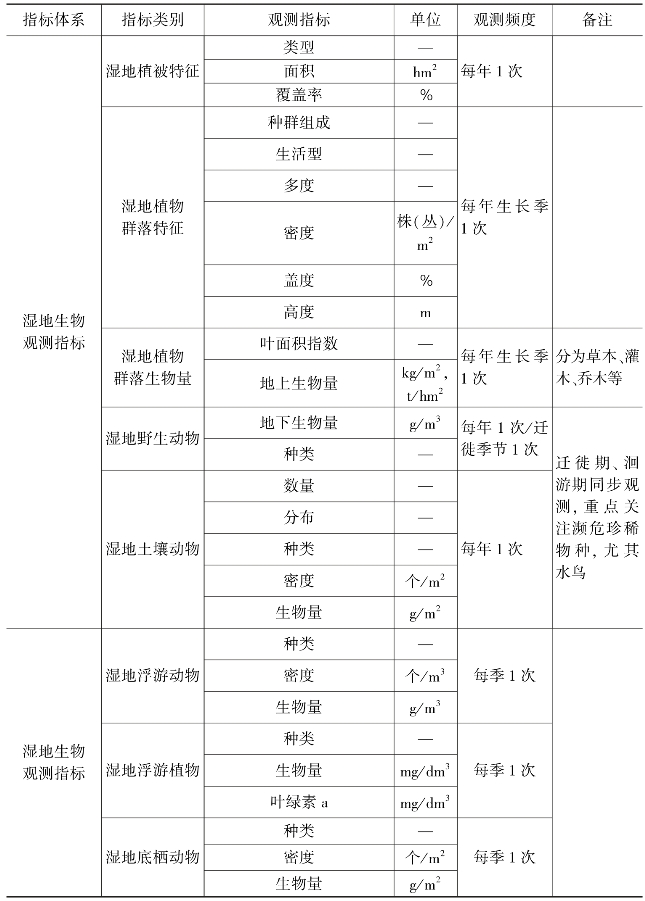
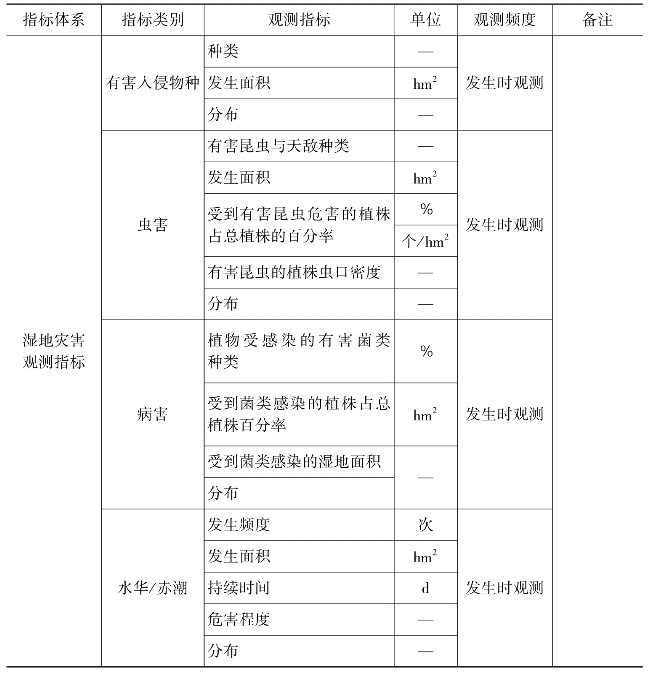
生态系统全要素监测在当前是数据采集发展新方向，其监测数据还应包括气象、土壤、径流数据等，如贺兰山生态观测研究站油松林样地、青海云杉林样地、针阔混交林（山杨＋油松＋青海云杉）样地群落物种、地表径流量、土壤含水量、大气降水水质、穿透雨水质测定、地表径流水质测定、地下水径流水质测定、土壤物理化学性质、土壤微生物的测定，宁夏黄河湿地水土气生生态要素长期观测等，表13-1、表13-2以国家林草局发布的森林生态系统定位观测各要素观测指标和湿地生态系统定位观测各要素观测指标为例，说明两类不同类型生态系统观测的指标体系和各生态要素的观测指标，供大家参考。
表13-1 森林生态系统定位观测各要素观测指标
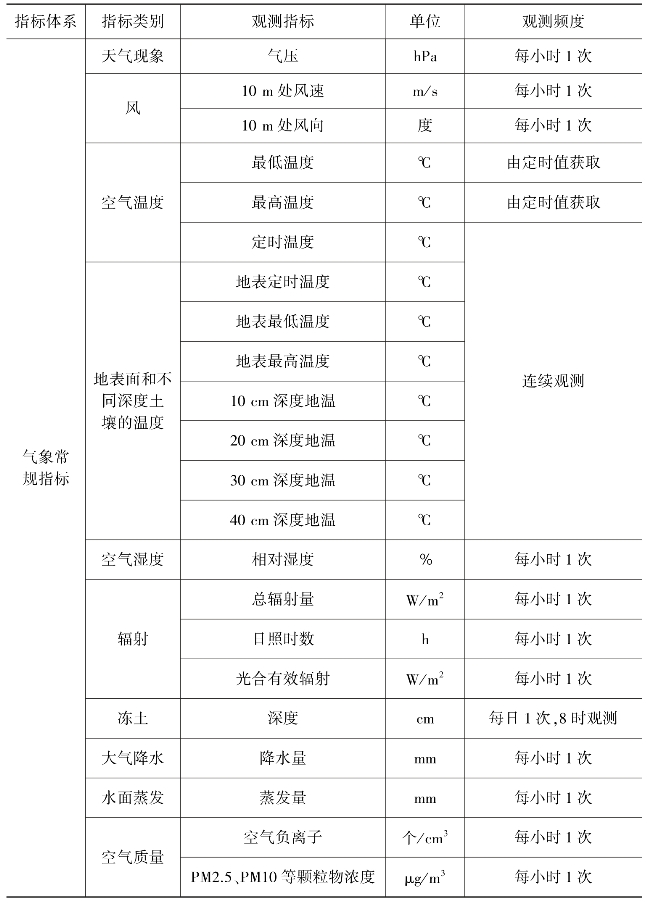
续表
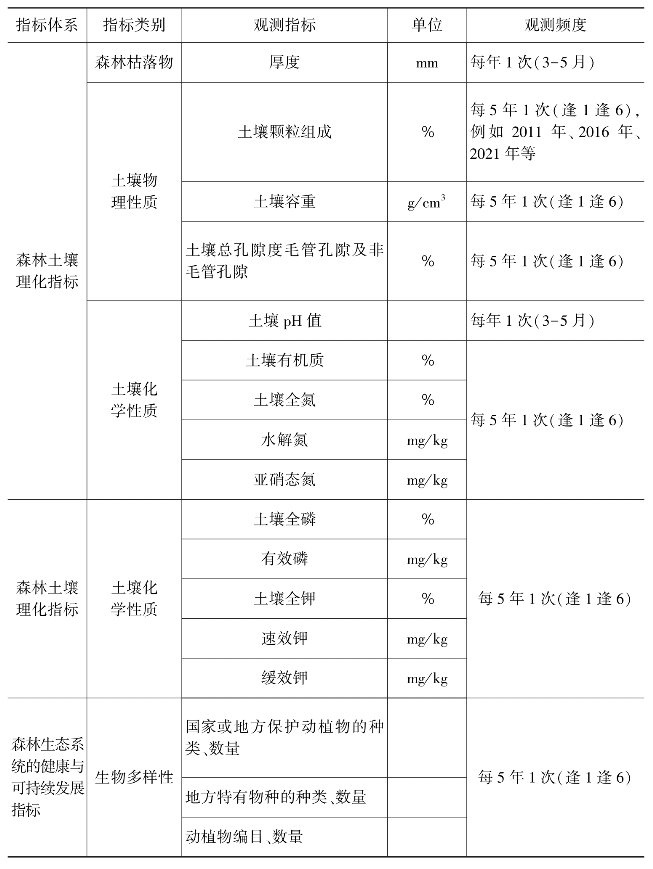
续表
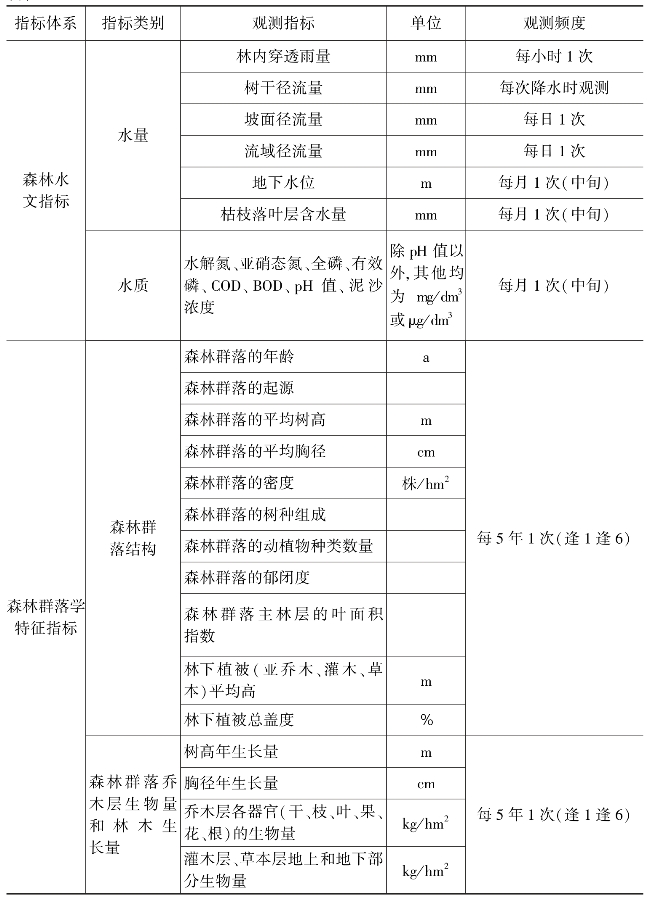
续表
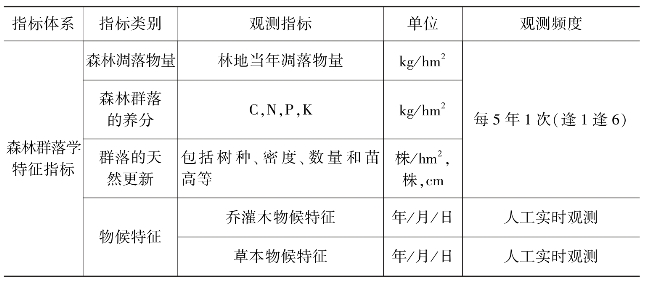
表13-2 湿地生态站基本观测指标清单
续表
续表
续表
(www.chuimin.cn)
续表
续表
在生态学基础研究中，多数都是通过一次性或者阶段性取样收集数据，取样的目的是通过样方的研究准确推测群落的总体，抽取的这一部分成为取样单位，包括样方、样点、样线、样带等，同时还需获取样方中生物分布和环境因子数据。
在建设永久样地和临时样地过程中，取样并采集数据的方法包括主观取样（设置样地）和客观取样（设置样地）法，这需要根据生态学研究或监测目的做出选择。
关于野外生态调查、取样和数据采集，由于涉及植物个体的生理指标、种群、群落或者动物、微生物等不同的特殊要求，内容较多，而且也不是本书的重点，在此不展开详细叙述，请阅读相关书籍。
二、数据资料的整理
在实验研究中，通过人工观测和利用仪器设备定期采集，可获得大量的原始数据资料。这些资料往往是凌乱的，无规律性可循。只有通过对资料的整理，才能发现其内部联系和规律性。首先需要对数据资料手工录入成电子文档，或者将野外大量的监测数据比如气象数据、水文数据等通过专用软件导入电脑中，进行分类，再做整理。
1．数据资料分类。首先对数据资料进行另行鉴别，划分为不同类型的生态数据，明确数据资料的特点，为后续数据分析提供方向。
2．数据资料的检查与核对。检查、核对原始资料的目的在于确保原始资料的完整性和正确性。完整性是指原始资料无缺失或者重复、特大、特小的异常数据（需结合专业知识进行判断）。对于有重复、异常或遗漏的数据，应予以删除或补齐；对于有错误、相互矛盾的数据应进行更正，必要时进行复查或者重新试验。原始数据的检查、核对，是生态学研究中一项非常重要的工作，因为只有完整、正确的数据，才能真实地反映出试验的客观情况，通过数据分析得出可靠的结论。
3．数据整理的方法。首先制作数据表，由标题、横标目、纵标目、线条、数字构成，其基本格式如下：
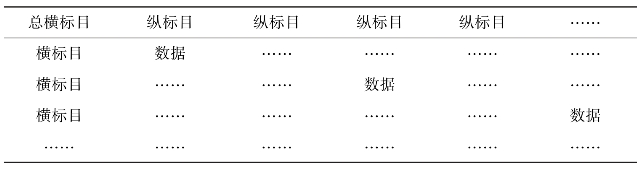
标题要简明扼要，能准确地说明表的内容，有时需注明时间、地点。
标目分横标目和纵标目两项。横标目在表的左侧，用以表示被说明事物的主要属性或指标，纵标目列在标的上端，说明横标目个观测属性指标的内容，并注明单位，如百分数（%）、千克（kg）、公顷（hm）等。
数字一律用阿拉伯数字，数字以小数点对齐，小时位数一致，无数字的用“—”表示，数字是“0”的，则填写“0”。
目前学术论文投稿都流行三线表。如果在Word文档里面，表格的纵向线条可省略，Excel录入数据则用自动生成的线条即可。
其次，对进行方差分析的数据，应检查是否符合方差分析的基本前提或基本假定。进行方差分析的数学模型均为线性可加模型，这个模型明确提出了处理效应与误差效应应该是“可加的”，正是由于这一“可加性”，才有了样本平方和的“可加性”，也就有了试验观测值总平方和的“可分解性”。如果试验资料不具备这一性质，变量的总变异依据原因的分解将失去根据，方差分析不能正确进行。但是，有数据就其性质来讲，不符合方差分析的基本假定，其中最常见的一种情况是处理平均数和处理内均方有一定关系（如二项分布数据），对这类资料不能直接进行方差分析，而应考虑采用非参数方法分析或进行数据转换后再做方差分析。
有关生态数据分析与建模的文章
- 详细阅读
-
优化基础数据采集及处理方法详细阅读
用户画像涉及大量的数据处理和特征提取工作，往往需要用到很多数据源，且多人并行处理数据和生成特征。在基础数据采集方面，可以通过列举法，先列举出构建用户画像所需要的基础数据。图9-2用户数据图静态信息数据为用户相对稳定的信息，主要包括人口属性、商业属性等方面数据。数据采集完后还要对其进行处理，主要是清洗无用数据，并将获取的数据进行规范化处理，使之可以在分析建模中可以直接被应用。......
2023-06-28
-
数据采集硬件概述详细阅读
数据采集硬件是计算机和外界之间的接口。有些数据采集设备仅拥有上述功能中的一种，很多数据采集设备还拥有实现测量系统和过程自动化的其他功能。数据采集设备可用于最常用的计算机总线，包括USB、PCI、PCIExpress和以太网。最近，数据采集设备已可用于802.11无线网络进行无线通信。表3-4列出了常用数据采集总线的选择指南。......
2023-07-02
-
CANOCO排序方法-生态数据分析详细阅读
3．一个数据集被另一个数据集解释后，再被第三个数据解释——偏典范排序。图16-1CANOCO分析数据的一般流程1．排序模型的决定。表16-1基本排序方法和排序模型对照表3．CanoDraw作图。......
2023-11-17
- 详细阅读
-
数据采集基本原理解析详细阅读
数据采集系统中采用计算机作为处理机。因此，在数据采集系统中同时存在着两种不同形式的信号：离散数字信号和连续模拟信号。为了避免产生上述问题，在对模拟信号离散化时，必须依据采样定理规定的原则进行。而脉冲函数：图3-4 采样过程原理图a）采样信号 b）脉冲函数2.采样定理对于一个有限频谱的连续信号，当采样频率大于信号成分最高频率的2倍时，采样才能不失真地恢复到原来的连续信号。采样定理是采样频率选取的理论基础。......
2023-07-02
-
数据采集系统配置步骤详解详细阅读
根据仪器对数据采集装置的技术要求的不同，可以构成不同结构的数据采集装置，这就要求能按照需求去构成一个具有高性价比的数据采集系统。在确定数据采集系统的结构时，需要认真考虑参数变化的速率、分辨率、精度和通道数等问题。图6-4分时采集系统的另一种结构形式2.同时采集系统同时采集系统的结构形式如图6-5所示，每个通道有一个IA和一个ADC。由于各个通道能同时进行A/D转换，因此，这种方案适用于高速的数据采集系统。......
2023-06-22
-
生态数据分析与建模：数据标准化方法及实例详细阅读
为了消除量纲影响和变量自身变异大小和数值大小的影响，故将数据标准化。经过标准差标准化后，数据都是没有单位的纯数量。尽管如此，它还是当前用得最多的数据标准化方法，也是SPSS中最为常用的标准化方法。即第三步，再对变量进行标准差标准化，即将某变量中的观察值减去该变量的平均数，然后除以该变量的标准差。表13-7长江17个观测点的水质分析表数据转换步骤如下：1．数据的标准化处理。......
2023-11-17
相关推荐