首页理论教育生态数据分析与建模：对数函数曲线及其应用

生态数据分析与建模：对数函数曲线及其应用

2023-11-17 理论教育版权反馈

【摘要】：如果两个变量的成对观测值在坐标系中的散点图分布趋势类似于对数函数曲线见图8-3，可配合对数曲线方程＝a＋blg x。图8-3对数曲线＝a＋blg x的图像［例10］在大棚育苗中，塑料薄膜苗床内空气最高温度和室外空气最高温度资料如表8-1所示。表8-1苗床内最高温度（y，℃）与空气最高温度（x，℃）的关系图8-4苗床内最高气温y与空气最高气温x的关系图8-5例18资料x′与y之间的直线关系2．配合对数函数方程。

对数函数（logarithmic function）的一般表达式为

若令lg x＝x′，则式（8-11）可以写成：

式（8-12）即为式（8-11）直线化后的表达形式。

如果两个变量的成对观测值在坐标系中的散点图分布趋势类似于对数函数曲线见图8-3，可配合对数曲线方程＝a＋blg x。首先将x变量的每一观测值取对数转换为新变量x′，然后用x′与y进行直线回归分析，求得a和b，即得到对数函数方程。

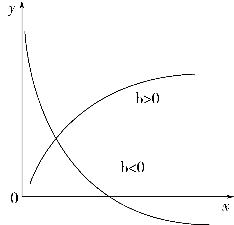
pagenumber_ebook=78,pagenumber_book=66

图8-3　对数曲线 pagenumber_ebook=78,pagenumber_book=66 ＝a＋blg x的图像

［例10］在大棚育苗中，塑料薄膜苗床内空气最高温度和室外空气最高温度资料如表8-1所示。试求它们之间的函数关系式。

1．绘制散点图，判断曲线类型。

根据表8-1资料绘出（x，y）的散点图见图8-4，与图8-3中b＞0的曲线相似。为了能够作出更准确的判断，图8-5绘出了（x′＝lg x）与y的散点图，x′与y之间存在直线关系，这说明选择对数曲线是适合的。

表8-1　苗床内最高温度（y，℃）与空气最高温度（x，℃）的关系

pagenumber_ebook=79,pagenumber_book=67

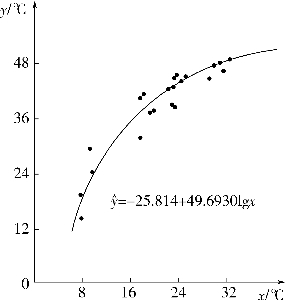
pagenumber_ebook=80,pagenumber_book=68

图8-4　苗床内最高气温y与空气最高气温x的关系

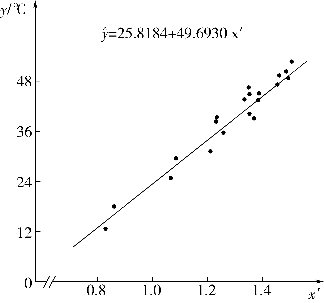
pagenumber_ebook=80,pagenumber_book=68

图8-5　例18资料x′与y之间的直线关系

2．配合对数函数方程。

利用x（x′＝lgx）和y进行直线回归分析，得到a和b值，并代入式（8-11）即得对数函数方程。(www.chuimin.cn)

具体步骤如下所述：

第一步，根据表8-1资料计算6个一级数据：

第二步，由一级数据计算5个二级数据：

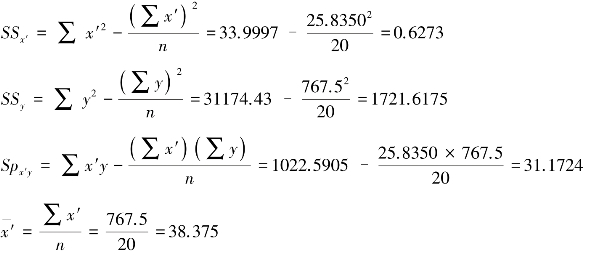
pagenumber_ebook=81,pagenumber_book=69

第三步，计算回归系数b和回归截距a：

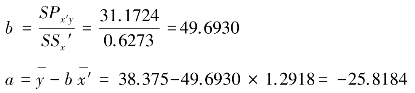
pagenumber_ebook=81,pagenumber_book=69

第四步，将a和b直接代入式（8．12），得到y与x的对数函数方程：

3．直线化回归方程的显著性检验。

计算y与x′直线回归关系的回归与离回归平方和：

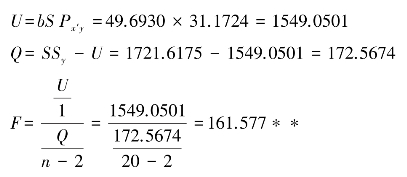
pagenumber_ebook=81,pagenumber_book=69

F＝161．577＞F0．01，说明回归关系极显著，配合对数函数方程是适合的（表8-2）。

表8-2　　例19资料中y与x′回归关系的显著性检验

pagenumber_ebook=82,pagenumber_book=70

利用曲线回归方程进行预测时，可将每一个x值转换成x′再通过回归分析方法预测出y所在区间。表8-2中最后一列即为每一个x值代入曲线回归方程得到相应的y估计值 pagenumber_ebook=47,pagenumber_book=35 。