在一定的显著性水平下统计检验原假设：模型为实测样本的推论总体。柯尔莫哥洛夫非参数检验法：是利用样本经验分布和推论总体分布间的最大差异作为检验统计量式中：Fn为样本经验分布；Fo为推论总体分布。大量模拟样本，其长度等于实测样本长度，计算各模拟样本的参数：均值、方差、偏态系数，自相关系数等，绘制参数的经验分布，求得相应于频率2.5%和97.5%的参数值，作为置信上、下限。......
2025-09-30
偏相关分析及显著性检验
【摘要】：偏相关分析就是在研究多个相关变量间的关系时，固定其他变量不变而研究其中某两个变量直线相关程度与性质的统计分析方法。3个相关变量x1，x2，x3的一级偏相关系数共有3个，记为r12·3、r13·2、r23·1。四个相关变量x1，x2，x3，x4的二级偏相关系数共有C3＝6个，记为r12·34，r13·24，r14·23，r23·14，r24·13，r34·12。［例9］检验［例8］所得偏相关系数的显著性。检验结果与t检验一致。
多个相关变量间的关系是较为复杂的，其中任何两个变量间常常存在不同程度的直线相关，但是这种相关又包含有其他变量的影响。此时，直线相关分析并不能真实反映两个相关变量间的关系，只有消除了其他变量的影响之后，研究两个变量间的相关，才能真实反映这两个变量间直线相关程度与性质。偏相关分析就是在研究多个相关变量间的关系时，固定其他变量不变而研究其中某两个变量直线相关程度与性质的统计分析方法。
一、偏相关系数的意义及计算
（一）偏相关系数的意义
在多个相关变量中，其他变量保持固定不变，所研究的两个变量间的直线相关称为偏相关（partial correlation）。用来表示两个相关变量偏相关的程度与性质的统计数叫偏相关系数（partial correlation coefficient）在偏相关分析中，根据被固定的变量个数的多少将偏相关系数分级，偏相关系数的级数等于被固定的变量的个数。
当研究两个相关变量x1，x2的关系时，用直线相关系数r12表示x1与x2直线相关的程度与性质。此时固定的变量个数为0，所以直线相关系数r12又叫作零级偏相关系数
当研究3个相关变量x1，x2，x3两两间的相关时，须将其中的1个变量固定不变，研究另外两个变量间的相关，即此时只有一级偏相关系数才真实地反映两个相关变量间直线相关的程度与性质。3个相关变量x1，x2，x3的一级偏相关系数共有3个，记为r12·3、r13·2、r23·1。
当研究四个相关变量x1，x2，x3，x4两两间的相关时，须将其中的两个变量固定不变，研究另外两个变量间的相关，即此时只有二级偏相关系数才真实地反映两个相关变量间直线相关的程度与性质。四个相关变量x1，x2，x3，x4的二级偏相关系数共有C3＝6个，记为r12·34，r13·24，r14·23，r23·14，r24·13，r34·12。
一般，当研究M个相关变量x1，x2，…，xM两两间的相关时，须将其中的M-2个变量保持固定不变，研究另外两个变量的相关才能真实地反映这两个相关变量间的相关，即此时只有M-2级偏相关系数才真实地反映这两个相关变量间直线相关的程度与性质。M个相关变量x1，x2，…，xM的M-2级偏相关系数共有
＝M（M-2）/2个xi与xj的M-2级偏相关系数记为rij（i、j＝1，2，…，M，i≠j）。
偏相关系数rij的取值范围为［-1，1］即-1≤rij≤1
（二）偏相关系数的计算
1．一级偏相关系数的计算。
设3个相关变量x1，x2，x3有n组实测值
二级偏向关系数可由一级偏相关系数计算，计算公式为
3．M-2级偏向关系数的计算。
设M个相关变量x1，x2，…，xm有n组观测值
M-2级偏向关系数rij，的计算方法如下。首先计算直线相关系数rij
其中，SPij＝∑（xi-xi）（xj-xj），SSi＝∑（xi-xi）2，SSj＝∑（xj，xj）2，并有直线相关系数rij组成相关系数矩阵R
然后求相关系数矩阵R的逆矩阵C
相关变量xi与xj的M-2级偏相关系数rij．的计算公式为
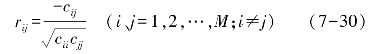(https://www.chuimin.cn)
［例8］根据［例5］的有关数据，计算偏相关系数ry1．2，ry2．1和r12．y。首先，根据［例5］的有关数据，计算直线关系数ry1，ry2和r12。
其次，将算得的各个rij代入式（7-24），即得偏向关系数
表明，x1和y、x2呈正偏向关；x1和x2呈负偏向关。当然，这些偏相关的显著性还有待检验。
二、偏相关系数的假设检验
（一）t检验
设相关变量xi与xj的总体偏相关系数为pij，则对偏相关系数rij．进行假设检验的无效假设与备择假设为：H0：pij＝0，HA：pij≠0
t检验计算公式为
其中，srij为偏相关系数标准误
n为观测值组数，M为相关变量总个数。
（二）查表法
由df＝n-M，查附表3，得，r0．01（n-M）。 将偏相关系数rij的绝对值与r0．05（n-M），r0．01（n-M）进行比较，做出统计推断：
若｜rij｜＜r0．05（n-M），P＞0．05，则偏相关系数rij不显著，或者说xi与xj偏相关不显著；
若r0．05（n-M）≤｜rij｜＜r0．01（n-M）＜p≤0．05，则偏相关系数rij显著，或者说xi与xj偏相关显著；
若｜rij｜≫r0．01（n-M），p≤0．01，则偏向关系数rij极显著，或者说xi与xj偏相关极显著。
［例9］检验［例8］所得偏相关系数的显著性。
采用t检验法，因为
由df＝n-M＝15-3＝12。查t值表，得t0．01（12）＝3．055，因为ty1·2、ty2·1、｜t12·y｜均大于t0．01（12），P＜0．01，所以上述3个偏相关系数都是极显著的，因为ry1·2＝0．8487＞0、ry2·1＝0．9204＞0、r12·y＝-0．9281＜0，所以，确切地说，产量y与穗数x1、每穗粒数x2呈极显著的正偏相关，而穗数x1与每穗粒数x2呈极显著的负偏相关。
若用查表法，由df＝n-M＝15-3＝12查附表3，得r0．05（12）＝0．532，r（0．0112）＝0．661，因为ry1·2＝0．848 7、ry2·1＝0．920 4、｜r12·y｜＝0．928 1均大于r（0．0112），P＜0．01，所以这3个偏相关系数都是极显著的。检验结果与t检验一致。
相关文章
- 详细阅读
- 详细阅读
-
共同方法偏差检验的分析介绍详细阅读
共同方法偏差，也叫同源性偏差，指的是由于同样的数据来源或者评分人、同样的测量环境、题项语境与题项本身特征，所造成的自变量与因变量之间人为的共变，共同方法变异是一种系统误差。我们对本研究中变量的所有题项一起做因子分析，在本文中，问卷所有题项解释总变异为62.332%，第一个因子仅解释变异量的13.569%，这表明没有单一的一个因子解释了绝大部分的变异量，因此，可以看到本研究数据的同源误差问题并不严重。......
2025-09-29
-
模具材料的进厂检验及要求详细阅读
因此，模具原材料进厂质量检验是确保模具质量的重要环节。原材料进厂检验一般应由工厂的检验部门负责，也可按供货合同规定检查验收。b.试样加热在炉控气氛中进行，在该温度的保持时间为5～15min，对Cr12Mo1V1钢应是10～20min。......
2025-09-29
-
实证结果分析,样本选择性偏误检验详细阅读
样本选择性偏误检验结果中逆mills比的估计值λ的P值为0.45，未能通过显著性检验，这表明该样本不存在选择性偏误问题，无需纠偏，可直接进行估计。是否纠纷通过1%的显著性检验，方向为正，符合预期假设。......
2025-09-29
-
电能表技术要求及检验方法详解详细阅读
注表11中括弧所列负载电流，系对供现场检验用的携带型精密电能表的要求。同时还应使电能表转数满足读数精度的要求，即转盘的最小分度与转数相比不应超过被检电能表基本误差规定值的1/5。......
2025-09-29
-
合格车辆检验，车况整洁，准时检验详细阅读
第十七条车辆必须经过车辆管理机关检验合格,领取号牌、行驶证,方准行驶。第十九条机动车必须保持车况良好、车容整洁。第二十条机动车必须按车辆管理机关规定的期限接受检验,未按规定检验或检验不合格的,不准继续行驶。第二十三条起重车、轮式专用机械车,不准拖带挂车或牵引车辆;二轮摩托车、轻便摩托车不准牵引车辆或被其他车辆牵引。......
2025-09-30
-
PC连接检验步骤及串口号配置详细阅读
下面进行PC连接操作。本实验机通过MAX232电平转换芯片与PC的串行接口连接。按H键并保持，按WR键同时抬起，显示“PC”，即表示实验机已准备好。在USB/RS232转换器连接到实验机后，必须确定新的串口号。若需连接单片机，只要将通信线的DB9插头连接到转换器的DB9插座，另一端连接实验机的通信插座即可。......
2025-09-30
相关推荐