复相关分析及相关指数R2

2023-11-17 理论教育版权反馈

【摘要】：，xm的线性相关分析。，xm的复相关指数，简称相关指数，记为R2，即相关指数R2表示多元线性回归方程的拟合度，或者说表示用多元线性回归方程进行预测和控制的可靠程度，显然0≤R2≤1。因复相关系数的假设检验与相应的多元线性回归关系的假设检验是等价的。

一、复相关系数的意义及计算

研究一个变量与多个变量的线性相关称为复相关分析。从相关分析角度来说，复相关中的变量没有因变量与自变量之分，但在实际应用中，复相关分析经常与多元线性国归分析联系在一起，复相关分析一般指因变量y与m个自变量x1，x2，…，xm的线性相关分析。

在多元线性回归分析中，如果m个自变量对因变量的回归平方和SSR占因变量y的总平方和SSy的比例越大，则表明因变量y和m个自变量的线性关系越密切，因此将SSR与SSy之比称为y与x1，x2，…，xm的复相关指数，简称相关指数，记为R2，即

pagenumber_ebook=67,pagenumber_book=55

相关指数R2表示多元线性回归方程的拟合度，或者说表示用多元线性回归方程进行预测和控制的可靠程度，显然0≤R2≤1。

相关指数R2的平方根称为因变量y与m个自变量x1，x2，…，xm的复相关系数（multiple correlation coefficient），即

pagenumber_ebook=67,pagenumber_book=55

复相关系数R表示y与x1，x2，…，xm的线性关系的密切程度。由于包含了x1，x2，…，xm的影响，因此，y与x1，x2，…，xm的复相关系数也就是y与的直线相关系数，即

显然，复相关系数的取值范围为：0≤R≤1。

二、复相关系数的假设检验

复相关系数的假设检验也就是对y与x1，x2，…，xm的线性关系的假设检验。因复相关系数的假设检验与相应的多元线性回归关系的假设检验是等价的。复相关系数R的假设检验有两种方法——F检验法与查表法。

（一）F检验

设p为y与x1，x2，…，xm的总体复相关系数，F检验的无效假设与备择假设为H0：ρ＝0，HA：ρ≠0。(www.chuimin.cn)

由下述统计数F检验复相关系数R的显著性

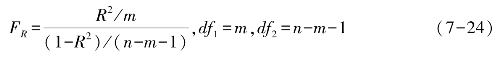
pagenumber_ebook=67,pagenumber_book=55

注意，因为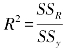 pagenumber_ebook=67,pagenumber_book=55 ，代入式（7-24）得

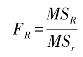
pagenumber_ebook=68,pagenumber_book=56

说明利用式（7-24）计算的FR值实际上就是多元线性回归关系假设检验——F检验计算的F值，也就是说复相关系数的假设检验与多元线性回归关系的假设检验是等价的。

（二）查表法

对于式（7-24），由于在df1、df2一定时，给定显著水平a的F值一定。因此可计算出相应于显著水平a时的临界R值

pagenumber_ebook=68,pagenumber_book=56

将其列成表，因此复相关系数的假设检验可用简便的查表法进行。具体做法是，由df1＝n-m-1和变量的总个数M＝m＋1，查附表3，得临界R值R0．05（n-m-1，M）、R0．01（n-m-1，M）将R与R0．05（n-m-1，M）、R0．01（n-m-1，M）比较，作出统计推断：

若R＜R0．05（n-m-1，M），p＞0．05，则y与x1，x2，…，xm的复相关系数R不显著，或者说y与x1，x2，…，xm的线性关系不显著；

若R0．05（n-m-1，M）≤R＜R0．01（n-m-1，M），0．01＜p≤0．05，则y与x1，x2，…，xm的复相关系数R显著，或者说y与x1，x2，…，xm的线性关系显著；

若R≥R0．01（n-m-1，M），p≤0．01，则y与x1，x2，…，xm的复相关系数R极显著或者说y与x1，x2，…，xm的线性关系极显著。