所以对于样本的回归方程,必须测定其来自无直线回归关系总体的概率大小。所以对直线回归的假设测验为H0:β=0对HA:β≠0由(6-3)式可推得回归系数b的标准误Sb为:而遵循ν=n-2的t分布,故由t值即可知道样本回归系数b来自β=0总体的概率大小。所以,对直线回归作假设测验,只需选择上述测验方法之一即可。......
2023-11-17
直线回归是回归分析中最简单的一种,又称为简单回归。
(一)直线回归方程
散点图上呈现直线趋势的两个变数,自变量x的每一个取值都有y的一个分布与之对应。在这种情况下,可以利用直线回归方程描述两个变数之间的关系:
![]()
其中x是自变量;![]() 是和x的两相对应的点估计值;a是x=0时的
是和x的两相对应的点估计值;a是x=0时的![]() 值,即回归直线在y轴上的截距,叫回归截距;b是x每增加一个单位时,
值,即回归直线在y轴上的截距,叫回归截距;b是x每增加一个单位时,![]() 平均地将要增加或减少的单位数,叫回归系数。
平均地将要增加或减少的单位数,叫回归系数。
使得![]() =a+bx最好地代表y和x在数量上的互变关系,根据最小二乘法:
=a+bx最好地代表y和x在数量上的互变关系,根据最小二乘法:
![]()
因此,分别对a和b求偏导数并令其为0,即可得到正规方程组

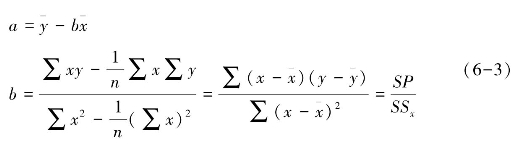
分子![]() 是x的离均差和y的离均差的乘积之和,简称乘积和(sum ofproducts),记作SP;分母是x的离均差平方和,记作SSx。将(6-2)式、(6-3)式算得的a和b值代入(6-1),即可保证
是x的离均差和y的离均差的乘积之和,简称乘积和(sum ofproducts),记作SP;分母是x的离均差平方和,记作SSx。将(6-2)式、(6-3)式算得的a和b值代入(6-1),即可保证![]() 为最小,同时使∑(y-
为最小,同时使∑(y-![]() )=0。
)=0。
a和b值皆可正可负,随具体资料而异。当a>0时,表示回归直线在I、II象限交于y轴;当a<0时,表示回归直线在Ⅲ、V象限交于y轴;当b>0时,表示y随x的增大而增大;当b<0时,表示y随x的増大而减小。若b=0或和0的差异不显著,则表明y的变异和x的取值大小无关,直线回归关系不能成立。
以上是a和b值的统计学解释。在具体问题中,a和b值将有专业上的实际意义。
将(6-2)式代入(6-1)式可得:
![]()
由(6-4)式可见,当x=![]() 时,必有
时,必有![]() ,所以回归直线一定通过
,所以回归直线一定通过![]() 坐标点。记住这一特性,有助于绘制具体资料的回归直线。
坐标点。记住这一特性,有助于绘制具体资料的回归直线。
由(6-4)式还可看出:①当x以离均差![]() 为单位时,回归直线的位置仅决定于
为单位时,回归直线的位置仅决定于![]() 和b;②当将坐标轴平移到以
和b;②当将坐标轴平移到以![]() 为原点时,回归直线的走向仅决定于b,所以一般又称b为回归斜率(regression slope)
为原点时,回归直线的走向仅决定于b,所以一般又称b为回归斜率(regression slope)
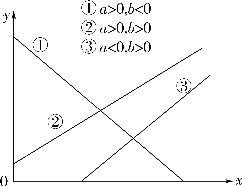
图6-1 直线回归方程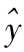 =a+bx的图
=a+bx的图
(二)直线回归方程的计算
以一个实例说明回归统计数计算的过程。
[例1]一些夏季害虫盛发期的早迟和春季温度高低有关。江苏武进连续9年测定3月下旬至4月中旬旬平均温度累积值(x,旬·度)和水稻一代三化螟盛发期(y,以5月10日为0)的关系,得结果于表6-1。试计算其直线回归方程。
表6-1 累积温和一代三化螟盛发期的关系
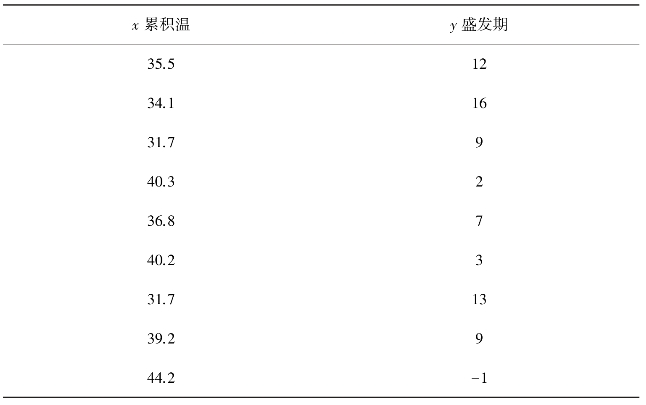
首先由表6-1算得回归分析所必需的6个一级数据(即由观察值直接算得的数据),
n=9
∑x=35.5+34.1+...+44.2=333.7
∑x2=35.52+34.12+...+44.22=12 517.49
∑y=12+16+...+(-1)=70
∗∑y2=122+162+...+(-1)2=794
∑xy=(35.5×12)+(34.1×16)+...+[44.2×(-1)]=2 346.4然后,由一级数据算得5个二级数据:
SSx=∑x2-(∑x)2/n=12 517.49-(333.7)2/9=144.635 6
∗SSy=∑y2-(∑y)2/n=794-(70)2/9=249.555 6(www.chuimin.cn)
SP=∑xy-∑x∑y/n=2436.4-(333.7X70)/9=-159.044 4
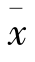 =∑x/n=333.7/9=37.077 8
=∑x/n=333.7/9=37.077 8
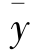 =∑y/n=70/9=7.777 8
=∑y/n=70/9=7.777 8
因而有:b=SP/SSx=-159.044 4/144.635 6=-1.099 6[天/(旬·度)]
a=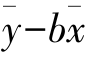 =7.777 8-(-1.099 6×37.077 8)=48.548 5(天)
=7.777 8-(-1.099 6×37.077 8)=48.548 5(天)
故得到表6-1资料的回归方程: =48.548 5-1.099 6x或化简成:
=48.548 5-1.099 6x或化简成: =48.5-1.1x
=48.5-1.1x
(三)直线回归方程的图示
直线回归图包括回归直线的图象和散点图,它可以醒目地表示x和y的数量关系。
制作直线回归图时,首先以x为横坐标,以y为纵坐标构建直角坐标系(纵、横坐标皆需标明名称和单位);然后取x坐标上的一个小值x1代入回归方程得![]() ,取一个大值x2代入回归方程得
,取一个大值x2代入回归方程得![]() ,连接坐标点(x1,
,连接坐标点(x1,![]() )和(x2,
)和(x2,![]() )即成一条回归直线。如例6-1资料,以x1=31.7代入回归方程得
)即成一条回归直线。如例6-1资料,以x1=31.7代入回归方程得![]() =13.69;以x2=44.2代入回归方程得
=13.69;以x2=44.2代入回归方程得![]() =-0.05。在图6-2上确定(31.7,13.69)和(44.2,-0.05)这两个点,再连接之,即为
=-0.05。在图6-2上确定(31.7,13.69)和(44.2,-0.05)这两个点,再连接之,即为![]() =48.5485-1.099 6x的直线图象。注意:此直线必通过点
=48.5485-1.099 6x的直线图象。注意:此直线必通过点![]() ,它可作为制图是否正确的核对。最后,将实测的各对(xi,yi)数值也用坐标点标于图6-2上。
,它可作为制图是否正确的核对。最后,将实测的各对(xi,yi)数值也用坐标点标于图6-2上。
图6-2的回归直线是9个观察坐标点的代表,它不仅表示了表6-1资料的基本趋势,也便于预测。如某年3月下旬至4月中旬的积温为40旬·度,则在图6-2上可查到一代三化螟盛发期的点估计值在5月14日-15日,这和将x=40代人原方程得到![]() =48.548 5-(1.099 6×40)=4.6是一致的。因为回归直线是综合9年结果而得出的一般趋势,所以其代表性比任何一个实际的坐标点都好。
=48.548 5-(1.099 6×40)=4.6是一致的。因为回归直线是综合9年结果而得出的一般趋势,所以其代表性比任何一个实际的坐标点都好。
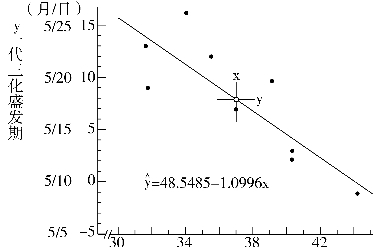
图6-2 旬平均温度累积值和一代三化螟盛发期的关系
(四)直线回归的估计标准误
由图6-2可见,满足Q=∑(y-![]() )2为最小的直线回归方程和实测的观察点并不重合,表明该回归方程仍然存在随机误差。Q就是误差的一种度代三化螟盛发期的关系量,称之为离回归平方和(sum of squares due to deviation from regres⁃sion)或剩余平方和。由于在建立回归方程时用了a和b两个统计数,故Q的自由度v=n-2。因而,可定义回归方程的估计标准误Sy/x为:
)2为最小的直线回归方程和实测的观察点并不重合,表明该回归方程仍然存在随机误差。Q就是误差的一种度代三化螟盛发期的关系量,称之为离回归平方和(sum of squares due to deviation from regres⁃sion)或剩余平方和。由于在建立回归方程时用了a和b两个统计数,故Q的自由度v=n-2。因而,可定义回归方程的估计标准误Sy/x为:
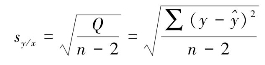
若各个观察点愈靠近回归线,将愈小(极端地说,当各观察点都落在回归线上时,若各观察点在回归线上下分散得愈远,则Sy/x愈大。故样本的Sy/x是回归精确度的度量,Sy/x愈小,由回归方程估计y的精确性愈高。
计算Sy/x的主要手续在于求Q。直接计算不仅步骤多、工作量大,而且若数字保留位数不够,会引起较大的计算误差。为简化手续,可从以下恒等式得出:

(五)直线回归的数学模型和基本假定
回归分析的依据是直线回归模型。在这一模型中,Y总体的每一个值由以下三部分组成:回归截距α;回归系数β;Y变数的随机误差ε。因此,总体直线回归的数学模型可表示为:
![]()
其中εj~N(0,![]() )。相应的样本线性组成为:
)。相应的样本线性组成为:
![]()
在按上述模型进行回归分析时,假定:
(1)Y变数是随机变数,而X变数则是没有误差的固定变数,至少和Y变数比较起来X的误差小到可以忽略。
(2)在任一X上都存在着一个Y总体(可称为条件总体),它是作正态分布的,其平均数μY/X是X的线性函数:
![]()
μY/X的样本估计值 ,
,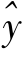 与X的关系就是线性回归方程(6-1)式。
与X的关系就是线性回归方程(6-1)式。
(3)所有的Y总体都具有共同的方差![]() ,这一方差不因X的不同而不同,而直线回归总体具有N(α+βX,
,这一方差不因X的不同而不同,而直线回归总体具有N(α+βX,![]() )。试验所得的一组观察值(xi,yi)只是N(α+βX,
)。试验所得的一组观察值(xi,yi)只是N(α+βX,![]() )中的一个随机样本。
)中的一个随机样本。
(4)随机误差ε相互独立,并作正态分布,具有N(0,![]() )。
)。
因此,模型中的参数共有a,即直线的截距;β,即直线的斜率;![]() ,误差的方差。其样本的相应估计值为a、b和
,误差的方差。其样本的相应估计值为a、b和![]()
理解上述模型和假定,有助于正确地进行回归分析。
有关生态数据分析与建模的文章

所以对于样本的回归方程,必须测定其来自无直线回归关系总体的概率大小。所以对直线回归的假设测验为H0:β=0对HA:β≠0由(6-3)式可推得回归系数b的标准误Sb为:而遵循ν=n-2的t分布,故由t值即可知道样本回归系数b来自β=0总体的概率大小。所以,对直线回归作假设测验,只需选择上述测验方法之一即可。......
2023-11-17

在多数生态学文献中,回归分析方面的问题是所有应用统计学中出现频率最高的问题。R2实际上是一个相对的度量,它表示回归平方和占总平方和的百分比。......
2023-11-17

表15-2数据视图中各类型的设定3.进行单因素方差分析。图15-6数据统计分析结果输出4.接下来再看方差齐性检验的结果。来自正态总体的两个样本进行均值比较常使用T检验的方法。同样是数据输入完成后,依次点击“分析—比较均值—独立样本T检验”。......
2023-11-17

式(7-1)就是多元线性回归的数字模型。(二)建立多元线性回归方程设y对x1,x2,…,m)称为高斯乘数,是多元线性回归分析假设检验与进一步统计分析所需要的。建立产量y与穗数x1、每穗粒数x2的二元线性回归方程。如果此回归关系是真实的,则可依据该二元线性回归方程由穗数x1、每穗粒数x2预测和控制产量y。统计学已证明,在m元线性回归分析中,离回归平方和的自由度为。......
2023-11-17

Origin是Windows平台下用于数据分析、项目绘图的软件,是科技工作者进行数据分析与科学绘图的高端软件作品,具有功能强大、使用方便的特点。Origin带给用户的是最直观、最简单的数据分析和绘图环境。Origin像Microsoft Word、Excel等一样,是一个多文档界面。Origin最突出的优点是使用简单,采用直观的、图形化的、面向对象的窗口菜单和工具栏操作。图17-1Origin的工作界面Origin目录下包括8个子目录,还有大量的模板文件和配置文件。......
2023-11-17

在完成建模过程之后,就是验证。对于验证可定义如下:如果模型运行符合建模者的要求,就可称模型已被验证。建模者必须多次重复该过程,直至验证和校准阶段的模型输出能使建模者满意。验证的这一部分在很大程度上是以主观标准为依据的。在验证阶段还应检查模型的长期稳定性。遗憾的是,由于缺乏时间,许多模型还没有经历适当的验证。因此,强烈建议在建模过程中的这一重要阶段,应花费足够的时间去验证并规划必要的资源分配。......
2023-11-17

灵敏度分析试图测量模型的一些参数、强制函数、状态变量初始值,或子模型对最重要状态变量的灵敏度。因此,对于参数P的灵敏度定义如下:S=[x/x]/[P/P]式中:x代表所考虑的状态变量。通常需要在两个或多个水平上发现参数变化的灵敏度,因为参数和状态变量之间的关系很少是线性的。如果发现所观察的状态变量对某个子模型很灵敏,应该考虑哪几个别的子模型可以替换使用,这些子模型应在野外或实验室做进一步的具体检验。......
2023-11-17

Origin提供两种菜单:全部菜单和简略菜单,默认值为全部菜单。工具栏中的图形按钮和菜单栏中的某一菜单功能相同,例如下图17-2。图17-2数字编辑区的快捷菜单要编辑的区域内点击右键,会出现对应区域的快捷菜单:1.工具栏。Origin为经常使用的菜单命令定制了按钮工具栏,每个按钮工具栏中的按钮只有当前窗口能使用到它时,它才被激活。......
2023-11-17
相关推荐