生态数据分析与建模：t分布及其特点

2025-09-30 理论教育版权反馈

【摘要】：t分布的平均数和标准差为：t分布密度曲线如图5-1所示，其特点是：图5-1不同自由度的t分布密度曲线1．t分布受自由度的制约，每一个自由度都有一条t分布密度曲线。2．t分布密度曲线以纵轴为对称轴，左右对称，且在t＝0时，分布密度函数取得最大值。3．与标准正态分布密度曲线相比，t分布密度曲线顶部略低，两尾部稍高而平。对于不同自由度下t分布的两尾概率及其对应的临界t值已编制成附表2，即t分布表。

由样本平均数抽样分布的性质知道：若x～N（μ，σ2），则～N（μ，σ2/n）。将随机变量标准化得：u＝（-μ），则u～N（0，1）。当总体方差σ2未知时，样本容量不大（n＜30）以样本标准差S代替σ所得到的统计量不再服从标准正态分布，而是服从t分布（t-distribution）。即：

pagenumber_ebook=39,pagenumber_book=27

式中，为样本平均数的标准误，计算公式为：

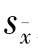pagenumber_ebook=39,pagenumber_book=27

pagenumber_ebook=39,pagenumber_book=27 为的估计值。

t分布的概率分布密度函数如下：

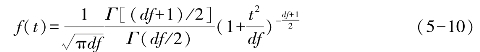
pagenumber_ebook=39,pagenumber_book=27

式中，t的取值范围是（-∞，＋∞）；df＝n-1；Γ为Γ函数。

t分布的平均数和标准差为：

t分布密度曲线如图5-1所示，其特点是：(https://www.chuimin.cn)

pagenumber_ebook=40,pagenumber_book=28

图5-1　不同自由度的t分布密度曲线

1．t分布受自由度的制约，每一个自由度都有一条t分布密度曲线。

2．t分布密度曲线以纵轴为对称轴，左右对称，且在t＝0时，分布密度函数取得最大值。

3．与标准正态分布密度曲线相比，t分布密度曲线顶部略低，两尾部稍高而平。df越小这种趋势越明显。df越大，t分布越趋近于标准正态分布。当n＞30时，t分布与标准正态分布的区别很小；n＞100时，t分布基本与标准正态分布相同；n→∞时，t分布与标准正态分布完全一致。

t分布的概率分布函数为：

因而t在区间（t1，＋∞）取值的概率——右尾概率为1-Ft（df）。由于t分布左右对称，t在区间（-∞，-t1）取值的概率也为1-Ft（df）。于是t分布曲线下由-∞到-t 1和由t 1到＋∞两个相等的概率之和——两尾概率为2（1-Ft（df））。对于不同自由度下t分布的两尾概率及其对应的临界t值已编制成附表2，即t分布表。该表第一列为自由度df，表头为两尾概率值，表中数字即为临界t值。

例如，当df＝15时，查附表2得两尾概率等于0．05的临界t值为t0．05（15）＝2．131，其意义是：P（-∞＜t＜-2．131）＝P（2．131＜t＜＋∞）＝0．025；P（-∞＜t＜-2．131）＋P（2．131＜t＜＋∞）＝0．05。

由附表2可知，当df一定时，概率P越大，临界t值越小；概率P越小，临界t值越大。当概率P一定时，随着df的增加，临界t值在减小，当df＝∞时，临界t值与标准正态分布的临界u值相等。

生态数据分析与建模：t分布及其特点

相关推荐