样本平均数分布|生态数据分析与建模

2023-11-17 理论教育版权反馈

【摘要】：样本平均数的分布与其他分布一样，有两个重要参数，一个是样本平均数的平均数，记作μ，另一个是样本平均数的方差，记作。标准误大，各样本平均数间差异程度大，样本平均数的精确性低。从某特定总体抽样，因为σ是一定值，所以只有增大样本容量，才能降低样本平均数的抽样误差。

由于从总体中抽出的样本为每一个可能样本，且每个样本中的变量均为随机变量，所以其样本平均数也为随机变量，也形成一定的理论分布，这种理论分布称为样本平均数的概率分布，或称样本平均数的分布（distribution of the sample mean）。

样本平均数的分布与其他分布一样，有两个重要参数，一个是样本平均数的平均数，记作μ pagenumber_ebook=45,pagenumber_book=33 ，另一个是样本平均数的方差，记作。根据抽样试验，可得出样本平均数分布的基本性质有：

进而有样本平均数的标准误差（standard error），简称平均数的标准误（standard error ofmean）：

标准误反映了样本平均数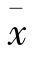 pagenumber_ebook=45,pagenumber_book=33 的抽样误差，即精确性的高低。

标准误大，各样本平均数间差异程度大，样本平均数的精确性低。

标准误小，各样本平均数间差异程度小，样本平均数的精确性高。(www.chuimin.cn)

标准误的大小与原总体的标准差σ成正比，与样本含量n的平方根成反比。

从某特定总体抽样，因为σ是一定值，所以只有增大样本容量，才能降低样本平均数的抽样误差。

3．如果从正态分布总体N（μ，σ2）进行抽样，其样本平均数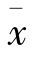 pagenumber_ebook=45,pagenumber_book=33 是一具有平均数μ，方差σ2/n的正态分布，记作N（μ，σ2/n）。

4．如果被抽总体不是正态分布总体，但具有平均数μ和方差σ2，当随样本容量n的不断增大，样本平均数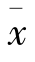 pagenumber_ebook=45,pagenumber_book=33 的分布也越来越接近正态分布，且具有平均数μ，方差σ2/n，这被称为中心极限定理。不论总体为何种分布，只要是大样本，就可运用中心极限定理，认为样本平均数的分布是正态分布，在计算样本平均数出现的概率时，样本平均数可按下式进行标准化：

样本平均数分布|生态数据分析与建模

相关推荐