首页理论教育平均数的计算方法及性质

平均数的计算方法及性质

2023-11-17 理论教育版权反馈

【摘要】：算术平均数可根据样本大小及分组情况而采用直接法或加权法计算。计算若干个来自同一总体的样本平均数的平均数时，如果样本含量不等，也应采用加权法计算。3．平均数的基本性质。用几何平均数比用算术平均数更能代表其平均水平。

平均数是统计学中最常用的统计量，用来表明资料中观测值的中心位置。平均数被广泛用来描述或比较各种技术措施的效果、某些数量性状的指标，等等。平均数种类较多，主要包括有算术平均数（arithmetic mean）、中位数（median）、大众数（mode）、几何平均数（geometric mean），以算数平均数最常用，现分别介绍如下。

一、算术平均数

算术平均数是指总体或样本资料中各观测值的总和除以观测值个数所得的商，简称平均数或均数，记为 pagenumber_ebook=45,pagenumber_book=33 。算术平均数可根据样本大小及分组情况而采用直接法或加权法计算。

1．直接法　主要用于样本含量n＜30以下、未经分组资料平均数的计算。

设某一资料包含n个观测值的样本：x1、x2、…、xn，则样本平均数 pagenumber_ebook=45,pagenumber_book=33 可通过下式计算：

其中，Σ为总和符号；表示从第一个观测值x1累加到第n个观测值xn。

当在意义上已明确时，可简写为Σx，（2-1）式即可改写为：

2．加权法　对于样本含量n≥30以上且已分组的资料，可以在次数分布表的基础上采用加权法计算平均数，计算公式为：

式中：xi—第i组的组中值；

fi—第i组的次数；

k—分组数。

第i组的次数fi是权衡第i组组中值xi在资料中所占比重大小的数量，因此fi称为是xi的“权”，加权法也由此而得名。

计算若干个来自同一总体的样本平均数的平均数时，如果样本含量不等，也应采用加权法计算。

3．平均数的基本性质。

（1）样本各观测值与平均数之差的和为零，即离均差之和等于零。

（2）样本各观测值与平均数之差的平方和为最小，即离均差平方和为最小。

或简写为：

对于总体而言，通常用μ表示总体平均数，有限总体的平均数为：

式中，N表示总体所包含的个体数。(www.chuimin.cn)

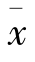当一个统计量的数学期望等于所估计的总体参数时，则称此统计量为该总体参数的无偏估计量。统计学中常用样本平均数作为总体平均数（μ）的估计量，并已证明样本平均数 pagenumber_ebook=45,pagenumber_book=33 是总体平均数μ的无偏估计量。

二、中位数

将资料内所有观测值从小到大依次排列，位于中间的那个观测值，称为中位数，记为Md。当观测值的个数是偶数时，则以中间两个观测值的平均数作为中位数。中位数简称中数。当所获得的数据资料呈偏态分布时，中位数的代表性优于算术平均数。中位数的计算方法因资料是否分组而有所不同。

1．未分组资料中位数的计算方法。对于未分组资料，先将各观测值由小到大依次排列。

（1）当观测值个数n为奇数时，中位数是第（n＋1）/2位置的观测值，即x（n＋1）/2为中位数。

（2）当观测值个数为偶数时，n/2和（n/2＋1）位置的两个观测值之和的1/2为中位数，即：

2．已分组资料中位数的计算方法。若资料已分组，编制成次数分布表，则可利用次数分布表来计算中位数，其计算公式为：

式中：L—中位数所在组的下限；

i—组距；

f—中位数所在组的次数；

n—样本含量；

c—小于中数所在组的累加次数。

三、众数

资料中最常见，或次数最多一组的中点值，称为众数，记为Mo。

四、几何平均数

n个观测值相乘之积开n次方所得的方根，称为几何平均数，记为G。它主要应用于农业生产动态分析。用几何平均数比用算术平均数更能代表其平均水平。

其计算公式如下：

为了计算方便，可将各观测值取对数后相加除以n，得lgG，再求lgG的反对数，即得G值，即