将一个二进制数转换成十进制数表示，只需按权展开做一次10进制运算即可以完成。将一个十进制数转换成二进制数表示，是数据转换中较复杂的工作。做乘、除运算时，其法则与十进制数也是相同的。它不同于数值运算。二进制数可以进行按位的逻辑运算，每位之间相互独立，位与位之间不存在进位和借位的关系。......
2023-11-07
单片机应用系统中的数制与编码
【摘要】：十进制数的位权是以10为底的幂，二进制数的位权是以2为底的幂，十六进制数的位权是以16为底的幂。各进位制中位权的值是基数的若干次幂。
所谓数制，就是多位数码中每一位的构成方法以及从低位向高位的进位规则。换个说法表述就是按进位原则进行计数称为进位计数制，简称“数制”。
1.4.1 进制数
我们在日常生活中大多使用十进制，即逢十进一，这主要是由人们的使用习惯决定的。其实在生活中还有许多不同的进位制度，如时间的表示方法是六十进制，即一小时等于六十分钟，一分钟等于六十秒等，还有常用的表示数量的单位“一打”是十二进制等。在计算机中，常用的进位制度有二进制、十进制、八进制和十六进制。
1.二进制
二进制数由0和1两个符号来表示，基数为2，按逢2进1、借1算2的规则计数。例如：10110011 1010 1111000010101101。
2.十进制
十进制数由0、1、2、3、4、5、6、7、8、9十个数字符号表示，基数为10，按逢10进1、借1算10的规则计数。例如：128，23，47，335。
3.八进制
八进制数由0、1、2、3、4、5、6、7八个数字符号表示，基数为8，按“逢8进1、借1算8”的规则计数。例如：70 360 777。
4.十六进制
十六进制数由0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F十六个数字符号表示，基数为16，按逢16进1、借1算16的规则计数。在C语言中表示十六进制数时，大小写字母的含义相同。例如：EF08 5ac 7BF。
5.数的“位权”概念
对十进制数335来说，百位上的3表示3个102，即300；十位上的3表示3个101，即30；个位上的5表示5个100，即5。
对二进制110来说，高位的1表示1个22，即4；低位的1表示1个21，即2；最低位的0表示0个20，即0。
可见，在数制中，各位数字所表示值的大小不仅与该数字本身大小有关，而且还与该数字所在位置有关，这就是数的“位权”。
十进制数的位权是以10为底的幂，二进制数的位权是以2为底的幂，十六进制数的位权是以16为底的幂。数位由高向低，以降幂的方式排列。
总的来讲，无论哪种数制都有共同的“逢n进一”计数运算规律和“位权表示法”特点。n是指数制中所需要的数字字符的总个数，称为基数，例如，十进制的基数是10（数字字符的个数是10个），二进制的基数是2（数字字符的个数是0、1两个）等。数字的值与它处在的位置是确定，这个固定的位置上的值称为位权。
“位权表示法”特点用来进行数制间的转换。
读一读：
计算机中的数据表示均采用二进制数，这是因为二进制数具有以下特点：
（1）二进制数中只有0和1两个数字，因此可用二进制数表示具有两个不同稳定状态的元器件。例如，电路中有、无电流，有电流用“1”表示，则无电流用“0”表示。类似地，还比如电路中电压的高低，晶体管的导通、截止等。
（2）二进制数运算简单，大大简化了计算机中运算部件的结构。如果进制数的基数用n表示，则它们的加法、乘法运算规律条数可以用下式表示：
由上式可知，基数n的取值越小，则其运算规律越少。二进制数的加法和乘法运算规律中有3条，而十进制数加法和乘法运算规律各有55条。所以计算机中使用二进制数进行运算容易实现。
二进制数的加法和乘法运算规则如下：
0＋0＝0 0＋1＝1＋0＝1 1＋1＝10
0×0＝0 0×1＝1x0＝0 1×1＝1
（3）二进制数的两个数字0和1与逻辑代数的逻辑量取值一致，从而可以采用二进制数进行逻辑运算。这样可以应用逻辑代数作为工具来分析和设计计算机中的逻辑电路，使逻辑代数成为计算机设计的数学基础。
1.4.2 进制数之间的转换
将数由一种数制转换成另一种数制称为数制间的转换。计算机在使用数据之前先必须把其他的数制转换成计算机所能接受的二进制数，计算机在运行结束后，再把二进制数转换为人们习惯的其他数制输出。
各进位制中位权的值是基数的若干次幂。因此，用任何一种数制表示的数都可以写成按位权展开的多项式之和。设一个基数为D的数值K， K = (Kn -1 K n - 2 … K1K0 K -1 … K-m )，则K的展开为(www.chuimin.cn)
对于二进制、十进制和十六进制，其基数D分别为2、10、16。
进制转换举例：
1.二进制数转换为十进制数
二进制数转换为十进制数只需每位数按位权展开多项式相加即可将二进制数1011转换成十进制数。
（1101）2＝1×23＋1×22＋0×21＋1×20＝8＋4＋0＋1＝(13)10
2.十进制数转换为二进制数
一个十进制整数要转化为二进制数，只需将该数反复除以2，其转换过程所得余数（从最后一个余数先读起）就是二进制数的表示形式。
一个十进制的小数要转化为二进制数，将该数乘以2，取乘积整数部分为相应的二进制数小数点后的最高位，再将乘积的小数部分乘以2，得次高位，如此反复直至小数部分为0或小数点后的位数达到精度要求为止。如一个十进制数既有整数又有小数部分，可按上述操作进行转换，然后进行连接。例如，将（57）10转换为二进制数。
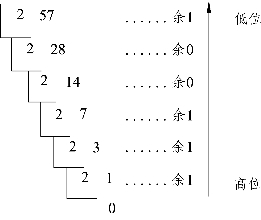
得到：
（57）10＝（111001）2
对于不同进制的数字间的转换在这里不做太多的叙述，对于初学者来讲，使用PC中的计算器来进行不同进制数字间的转换是一个方便快捷的办法，计算器的使用如图1-48所示。打开计算器软件，在“查看”下面设置，如要将十进制数“254”转换成二进制数，可以首先在计算器中选择十进制，输入数字“254”，再用鼠标单击选择二进制，这时计算器中即可显示经转换后的二进制数“11111110”。
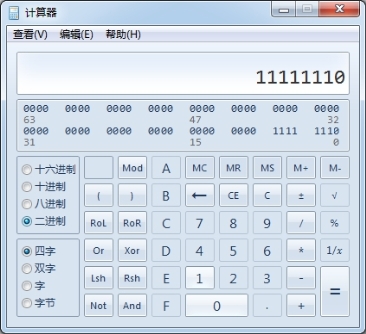
图1-48 使用计算器进行进制转换
1.4.3 数的编码
在计算机内部，所有的信息都要使用二进制的方法来表示，因为二进制的0和1两个数字恰好与存储单元的“有”和“无”相对应。不仅如此，数的符号“＋”或“－”也需要用二进制数来表示，在通常情况下，用0表示正数的符号“＋”，用1表示负数的符号“－”。当数的符号和数值表示方法使用二进制时，这样的数被称为“机器码”。
1.带符号数的编码
机器码有不同的码制，对应不同的表示方法，常用的码制有原码、反码和补码三种。
（1）原码：原码用最高位表示数的符号位，数值部分用二进制的绝对值表示。
（2）反码：正数的反码与其原码相同，负数的反码是将符号位除外，其他各位按位取反。
（3）补码：正数的补码与其原码相同，负数的补码是其反码加1。
数的原码、反码和补码的表示方法见表1-11。
表1-11 数的原码、反码和补码
2.二-十进制编码（BCD）
计算机中的数据处理是以二进制数运算法则进行的。二进制数不直观、易出错，因此在计算机的输入、输出中希望以人们熟悉的十进制数形式进行。适合于十进制数的二进制编码的特殊形式，即二进制编码的二进制数，简称BCD码。BCD码是用4位二进制数给十进制数0～9十个数进行编码，称之为二-十进制数。
3.ASCII码
在计算机中除数字用二进制数表示外，字母和各种字符也必须用二进制数形式表示。目前，最普遍使用的为ASCII码。
ASCII码是美国信息交换标准码（American Standard Code for Information Interchange）的缩写，它采用7位二进制代码对字符进行编码，可以表示128个字符。
有关单片机原理与应用 基于C语言的文章
- 详细阅读
-
单片机原理与应用中C语言串行口应用详细阅读
使用查询标志位的方法通过串行口发送C语言的经典语句“hello World！”，在PC上运行串口调试助手软件接收此消息并在屏幕上显示出来。单击“打开串口”按钮，这时会发现在串口调试助手的接收区有“hello World！”图9-29 串口调试助手向单片机发送数字单片机接收到来自PC发送的信息后，用LED灯显示该数字的状态，系统板的具体状态如图9-30所示。......
2023-11-17
-
机械零件-分类编码系统及应用详细阅读
至今为止，世界上已有几十种用于成组技术的机械零件编码系统，应用最广的是奥匹兹分类编码系统。该系统是1964年西德Aachen 工业大学H.OPITZ 教授领导开发的，很多国家以它为基础建立了各自的分类编码系统，如日本的KK-3 系统以及我国的JLBM-1 系统。图9-2JLBM-1 分类编码系统编码示例回转类零件——锥套 材料：45 钢（锻件）；非回转类零件——连接板 材料：HT150......
2023-06-29
-
单片机基础及应用:系统硬件设计详细阅读
1．系统的组成根据系统的主要技术指标和功能，本系统为一个8路数据实时采集系统，系统选用AT89C52单片机为主机。由于AT89C52片内具有8KB的程序存储器，所以系统不需要外部扩展程序存储器。2．系统的工作原理图10－16系统总体结构框图本系统设计采用定时采样控制方式进行工作，每隔0．5s对8路模拟量进行巡回采集1次。图10－19DAC0832的电压输出电路图打印机的选择在单片机系统中，经常选用微型打印机，如PP40、GP16等。......
2023-11-17
-
单片机原理与应用：采用KeiluVision详细阅读
Keil uVision软件是目前常用的单片机学习入门软件，要熟练掌握其主要功能。编程软件我们选用Keil uVision4的51版本，也叫作Keil C51。图2-7 安装完成最后，点击“Finish”，Keil uVision编程软件开发环境就安装好了。这里我们使用Keil uVision软件先打开一个工程，如图2-8 所示。Keil uVision软件本身都是有默认设置的，可以直接使用默认设置，也可以进行修改。图2-10 字体设置（二）现在以点亮一个LED灯为例来说明Keil uVision软件的初步使用。......
2023-11-17
-
单片机基础及应用中的复位电路与状态详细阅读
无论在单片机刚开始接上电源时，还是断电后或者发生故障后都要复位，所以必须清楚MCS-51单片机复位的条件、复位电路和复位后的状态。图2－12单片机常见的复位电路图图2－12为上电复位电路，它是利用电容充电来实现的。图2－12为按键复位电路。该电路除具有上电复位功能外，若要复位，只需按RESET键，此时电源VCC经电阻R1、R2分压，在RST端产生一个复位高电平。......
2023-11-17
-
单片机电源系统抗干扰措施，学习《单片机基础及详细阅读
单片机应用系统所使用的交流电源要与接有强电设备的动力线分开，最好从变电所单独拉一组专用供电线，或者使用一般照明电，这样可以减轻干扰的影响。如果采用磁饱和式交流稳压器，对来自电源的噪声干扰也有很好的抑制作用。此外还能检测电源瞬时短路和瞬时降压，同时产生复位信号。巧妙地利用该类芯片，可以提高单片机应用系统的可靠性。......
2023-11-17
-
单片机系统调试技巧及应用详细阅读
系统调试是硬件和软件设计过程中及之后非常重要的工作，以便排除软硬件故障，使软／硬件能协调工作。目的是检查电路板。调试对象不同应编制专门的测试程序，运行后检查输出是否一致。其次，脱机调试。插上CPU芯片，用示波器检查CPU的主要信号引脚是否正常。5）符号化调试。调试的步骤1）调试的顺序。3）中断模块的调试。仿真调试运行正常后，将软件固化到ROM中，则可脱机运行，系统研制完成。......
2023-11-17
相关推荐