首页理论教育个体X～N样本的均值与方差计算方法

个体X～N样本的均值与方差计算方法

2023-11-08 理论教育版权反馈

【摘要】：，Xn是总体X～N（0，1）的简单随机样本，，S2分别是样本均值与方差，求

一、选择题：1～8小题，每小题4分，共32分.每小题给出的四个选项中，只有一个选项是符合题目要求的，请将所选项前的字母填在答题纸指定位置上.

（1）x=0是函数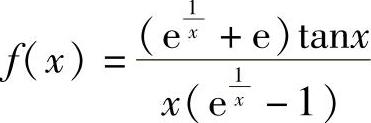的

（A）可去间断点；（B）跳跃间断点；

（C）无穷间断点；（D）第二类间断点，但不是无穷间断点.

[ ]

（2）设f（x）是连续函数，则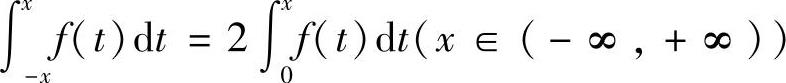是f（x）为偶函数的

（A）充分而非必要条件；（B）必要而非充分条件；

（C）充分必要条件；（D）既非充分又非必要条件.

[ ]

（3）级数

（A）绝对收敛；（B）条件收敛；

（C）发散；（D）收敛或发散与α取值有关.

[ ]

（4）记，其中

D₁={（x，y）|x²+y²≤1}，

D₂={（x，y）|（x-1）2+y²≤1}，

D₃={（x，y）|x²+（y-1）2≤1}，

则I₁，I₂，I3的大小满足

（A）I₁<I₂=I₃；（B）I₂=I₃<I₁；

（C）I₂<I₃=I₁；（D）I₃<I₂=I_1.

[ ]

（5）设A=（α₁，α₂，α₃，α₄）是四阶实对称矩阵，A^∗是A的伴随矩阵.如果（1，1，0，0）^T，（1，0，1，0）^T和（0，0，1，1）^T是方程组A^∗z=0的一个基础解系，则二次型f（x₁，x₂，x₃，x₄）=x^TAx（x=（x₁，x₂，x₃，x₄）^T）的标准形应形如

（A）a₁y²₁+a₂y²₂+a₃y²₃；（B）b₁y²₁+b₂y²₂；

（C）c₁y²₁；（D）d₁y²₁+d₂y²₂+d₃y²₃+d₄y²_4.

（其中，a₁，a₂，a₃，a₄，b₁，b₂，c₁，d₁，d₂，d₃，d₄都是非零常数）.

[ ]

（6）设矩阵方程AX=B（其中，A是m×n矩阵，B是m×l矩阵，X是n×l未知矩阵），则该方程有无穷多解的充分必要条件是

（A）r（A┊B）=r（A）=n；（B）r（A┊B）=r（A）<n；

（C）r（A┊B）>r（A）；（D）r（A┊B）=r（A）.

[ ]

（7）设X，Y是随机变量，其中X～N（1，1），概率密度为f₁（x）；Y的概率密度为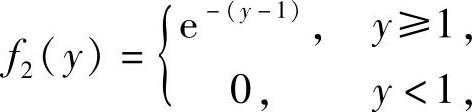记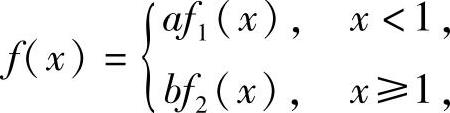则当f（x）是概率密度时，a，b应满足

[ ]

（8）设X₁，X₂，…，X_n是来自总体X～N（μ，σ²）的简单随机样本，其中，参数μ，σ2末知.记i，，则假设H₀：μ=0的t检验使用的统计量为

[ ](www.chuimin.cn)

二、填空题：9～14小题，每小题4分，共24分.请将答案写在答题纸指定位置上.

（9）函数f（x）=cos²x的二阶麦克劳林公式（带拉格朗日型余项）为____.

（10）对a>0，定积分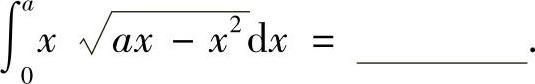

（11）微分方程（x²-1）dy+（2xy-cosx）dx=0满足y（0）=1的特解为____.

（12）设f（x，y）是连续函数，则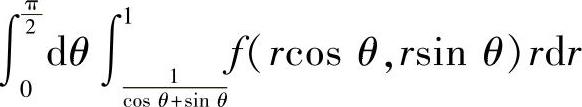在直角坐标系下的二次积分（先y后x）为____.

（13）设A是三阶矩阵，满足A³=E（三阶单位矩阵），记B=A²-A-2E，则B^-1关于E，A，A²表示式为____.

（14）设X₁，X₂，…，X₅是来自总体X～N（0，σ²）的一个简单随机样本，且统计量服从t分布，则正的常数a=____.

三、解答题：15～23小题，共94分.请将解答写在答题纸指定位置上.解答应写出文字说明、证明过程或演算步骤.

（15）（本题满分10分）

计算极限，其中

（16）（本题满足10分）

设f″（x）不变号，且曲线y=f（x）在点（1，1）处的曲率圆为x²+y²=2，证明函数f（x）在（1，2）内无极值点但有唯一零点.

（17）（本题满分10分）

设a₀=1，a₁=2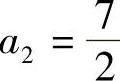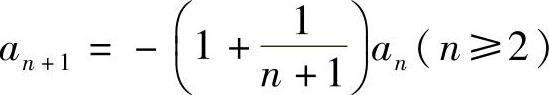，，，求幂级数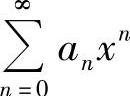的和函数s（x），并求定积分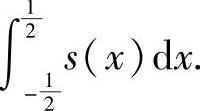

（18）（本题满分10分）

方程xe^2x-2x-cosx=0在（0，1）内的实根个数.

（19）（本题满分10分）

记曲面积分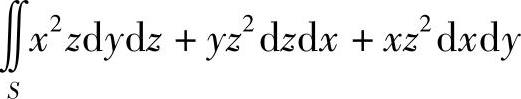（其中，S是曲面z=x²+y²（z≤1）的第一卦限部分上侧）的值为A，求满足f（0）=A，f′（0）=-A的二阶可导函数f（x），使得y[f（x）+3e^2x]dx+f′（x）dy是某个二元函数的全微分.

（20）（本题满分11分）

设α₁，α₂，α₃，α₄为四维列向量组，其中，α₁，α₂，α₃线性无关，α₄=α₁+α₂+2α_3.已知方程组

（α₁-α₂，α₂+α₃，-α₁+aα₂+α₃）x=α₄

有无穷多解.

（Ⅰ）求常数a的值；

（Ⅱ）对求得的a值，计算方程组的通解.

（21）（本题满分11分）

已知矩阵可相似对角化.

（Ⅰ）求常数a的值；

（Ⅱ）对（Ⅰ）中求得的a值，求正交变换x=Qy（其中，x=（x₁，x₂，x₃）^T，y=（y₁，y₂，y₃）^T，Q是正交矩阵），将二次型f（x₁，x₂，x₃）=x^TAx化为标准形.

（22）（本题满分11分）

设二维随机变量（X，Y）的概率密度为

（Ⅰ）求随机变量U=max{X，Y}的概率密度φ（u）；

（Ⅱ）求概率P（U≤EU）.

（23）设X₁，X₂，…，X_n是总体X～N（0，1）的简单随机样本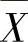，，S²分别是样本均值与方差，求