第十九章动物地球是动物和人类的家园虽然动物比植物灵活得多，受气候的影响也比植物小得多，但是，动物还是直接或间接地以植物为食物。社会依靠动物形成。还有一些鸟类，它们损害庄稼并以其他方式干扰人类活动。此外，还有一些会传播疾病、毁坏农作物的昆虫和微生物。米饭，当然是我们的主食，但是，我认为一些食用肉类，也是人的食物中必不可少的部分，因为它是维持人身体健康所必需的蛋白质、磷酸和其他元素的来源。......
2024-10-26
欧拉图解：动物与人的判断
【摘要】：用图解时，逻辑家大都着重外延方面，欧拉的图解是其一例。图二I型判断，即有些S是P、通常按欧拉的图解可用图三。例如“有些动物是人”这判断须用下面图四来表示：图四这里宾词则完全包含在主词外延之内为其一部分，因为“人”只是动物的一部分，即图四之部分2。每一类型的判断只需一图来表示。思维各种形式是相互联系的，所以表示判断的图解应该可按其原来的原则用于各种思维形式，如直接演绎推理与三段论式等。
传统的形式逻辑认为主谓判断是判断最典型的形式[3]。根据亚里斯多德的定义，判断是对于什么肯定或否定什么[4]。对之肯定或否定的什么称为主词，这概念以S来表示，以之肯定或否定的那个什么称为宾词，这概念以P来表示（S、P都是符号，源于拉丁语，不是亚里斯多德所原用的）。
我们在形式逻辑考察一个判断的两个概念的联系，可从两个不同的方面来看：（1）把概念的外延作为代表概念的东西；（2）把概念的内涵作为代表概念的东西。用图解时，逻辑家大都着重外延方面，欧拉的图解是其一例。
“所有人都是呼吸空气的”，这是一个全称肯定判断，即A 型判断。欧拉的图是（见图一）：
图一
图一很能表示S与P 的关系，S即“人”，这主词是完全包括在P“呼吸空气的”之内而为其一部分。
但图一不能概括所有A 型判断。例如“人是能制造劳动工具的哺乳动物”这一判断中，主词和宾词的外延是相等的。严格地讲，这种判断有别于上面的第一个例子，因为第一个例子的判断是涵蕴关系，而第二个例子的判断是相等关系。但传统形式逻辑将这两种判断都看为是A 型的判断，那么，A 型判断就不能只用上面的图一来表示。“人是能制造劳动工具的哺乳动物”的主词和宾词既相等，就必须用两个完全重合的圆如：
这里表示S的圆和表示P 的圆无异无别，故是重合，看来是同一个圆，因之，有图二。
图二
I型判断，即有些S是P、通常按欧拉的图解可用图三。
图三
这样两个交叉的圆以其部分2表示。如果I型判断只是像“有些学生是青年团团员”那种形式，这I就能够用了。却I型判断的“有些”尚未确定是多少，可能是主词外延的一部分，但又可能是全部，而意义未定，故云“有些”与“只有些”大异。就“有此”指概念外延一部分而言，上面图三亦不能完全表示I型判断。例如“有些动物是人”这判断须用下面图四来表示：
图四
这里宾词则完全包含在主词外延之内为其一部分，因为“人”只是动物的一部分，即图四之部分2。如果“有些”含有全部的可能，则I型判断须用图一、图二、图三、图四这四种图才能穷尽其义。
同样地，O 型判断，即有些S 不是P，也不能只用一个图来表示，因“有些”尚未确定为概念外延的一部分或其全部，而“不是”这否定系词是指判断对象S不具有宾词P 所指的属性，即S和P 完全隔开，通常是用欧拉下面的图即图五来表示：
图五
这里图五中是指交叉两图的部分1和P圆隔离，即部分1在P圆之外，但也可能有一种情况，P完全包含在S圆之内而为其一部分，则有些S仍在P图之外，如图六：
图六
这实质上就是上面的图四，却所指的不是部分2而是部分1，即有一部分的S是和P隔离的。
如果“有些”是未定之词而可能是全部的话，则需用下图七才能表示：
图七
图七表示S和P彼此完全隔离，这正是欧拉E 型判断的图，故O 型判断须用图五、图六、图七这三图，唯有E型判断只需图七就可表示其义。
由此可见，欧拉的图解，意义模糊，失掉图解的作用，而且这百年来沿用的图解只能勉强用之于判断，在判断之外，它是不能超任何作用的，所以是不正确而又限于很狭隘的范围的。（欧拉的整套图解可参看Paul Janét，Histoire de la philosophie，1927.pp.427－432。繁复不适用，兹不论列。）
图解的正确性有下列三个条件：
（1）作图的原则一经说明，则每图的意义当一目了然。
（2）每一个图只能有一个意义。
（3）每一类型的判断只需一图来表示。
思维各种形式是相互联系的，所以表示判断的图解应该可按其原来的原则用于各种思维形式，如直接演绎推理与三段论式等。
我们的图解是按上面的三个条件和原则拟定的。
兹先说明直言主谓判断的图解：
为表示判断中主词与宾词的关系，我们在一正方内作两个交叉的圆如下：（见图八）
图八
S圆与P圆交叉，正方表示S与P所隶属的极限，即范畴。正方为两交叉圆分成四部分，即1、2、3、4，其中的1显然是在S之内而在P之外，2是在S之内，同时也在P之内，3是在P之内而在S之外，4是同在S与P之外。
如果凡在S之外的用S（即“非S”）来表示，凡在P之外的用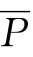
（即“非P”）来表示，那么，上图的1即SP，意即属于S而非P，同样地，2是SP，3是
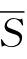P，而4是
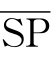[5]。
拿“所有人都是呼吸空气的”这一判断来作例子，则其中两个概念是“人”与“呼吸空气的”，S 表示“人”，而P 表示“呼吸空气的”，
表示“非人”，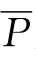
则表示“不呼吸空气的”，故图八中的四部分所指的是：
1即S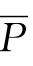
，指“人而不呼吸空气的”。
2即SP，指“人而呼吸空气的”。
3即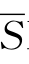
P指“呼吸空气的而非人”。
4即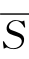
P指“即非人而又不呼吸空气的”。
现在我们看看“所有人都是呼吸空气的”这一A 型的判断该怎样用图来表示（见图九）。(www.chuimin.cn)
图九
“所有人都是呼吸空气的”这一判断是指“没有人而不呼吸空气的”，也就是说，“人而不呼吸空气”的东西是不存在的，也就是说，根据我们的认识，这种东西在客观现实中是没有的。如果我们用H 来表示不存在，我们就可以说图八中1部分，即SP，“人而不呼吸空气的”等于H。凡不存在的在图中用的斜线划掉，（见图九）故A 型判断既是“所有S都是P”，乃是说“S而不是P”是不存在的，其公式便是S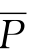
＝H[6]。
故“所有S是P”应意为SaP，公式是：S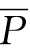
＝H。
E型判断的图如下（图十）：
图十
E型判断是“没有S和P”，（即任何S都不是P，）简写为SeP，其公式是：SP＝H，意即S而又P是不存在的。
I型判断是“有些S是P”，简写为SiP，其公式是：SP≠H，那就是说S而又P不是不存在，因为“有些S是P”显然是说，有些存在的东西是S而有P的属性的。
“不是不存在”即“存在”我们在图十一中用一星来表示，即“有些S是P”，即SP在图十一中是部分2。我们把＊放在2那一部分，如图十一。
图十一
这＊不论放在2任何位置都可，既有＊在这部分则绝不能再把这部分用斜线划掉表示它的不存在，否则自相矛盾。
O 型判断是“有些S不是P”，简写为SoP，其公式是：S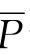
≠H，意即S而不是P这类东西不是不存在，即是存在的，因为“有些S不是P”，显然是说“S而不是P”是有的。这类型的判断可以用图十二来表示。
图十二
图十二中所表示的只是S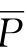
部分即1还存在的，故有＊在其内。
由上图九至图十二可以看出：
（1）A 与O，即图九与图十二，是矛盾的，这就是说，如A 真则O 假，O真则A 假；如A 假则O 真，O 假则A 真。
（2）同样地，E与I，即图十与图十一，是矛盾的，二者不能同时真，亦不能同时假，其一必真，果尔，则其另一必假。
由上面图九与图十又可看出：
（1）A 真则E必假，因为图九中1部分既经划掉（即A 是真），那么，再不容把2部分又划掉（以表示E 的真），如果1部分既已划掉而又划掉2部分，则S全部都被划掉，就是S 不存在，但S 是主词，表示判断的对象；我们绝不会对于不存在的东西有所肯定或否定。
（2）同样地，如果E真，图十中证明A 不能同时亦真，即A 必假。
（3）但是如果A 假，则图九中的1部分不能划掉，就是说这部分所表示的不是不存在，而是存在的，故必须划上＊，却1部分有＊并不能因之而划掉S的一部分即2部分以表示E 的真，但亦不能因之而确定2部分是代表什么存在的东西，所以由A 的假，图九中没有什么可证E 之真或假，A 假则E是不定的。
（4）同样地，如E假，即图十中2部分不能划掉而须放上＊，亦不能在图十中看出A 的真或假。
传统形式逻辑从判断的关系对于A 和E 所得的结论正如上述。A与E既有对立关系，两者不能同时真，但可能同时假。
由图九至图十二又可看出：
（1）如果A 真则1部分划掉，这部分既划掉以表示其所指的是不存在的，故2部分必存在，否则S全部不存在，故A 真则I亦必真，却从A之假，即从未划掉而有＊的1部分不能知2部分划掉与否，故从A 之假不能由图九中看出I之真或假，这也是传统形式逻辑的结论。
（2）同样地，从图十中，可见由E 之真而知O 之必真，却不能由E 之假而得出对于O 的任何确定结论。
（3）反之，如I真，图十一中2部分有＊以表示SP 的存在，但不能由此而看出1部分是怎样，所以A 的真假是未定的，但如果I是假，即2部分不能有＊，则需划掉，故E 必真，而E 假，则1部分是划掉或不划掉莫由决定，故O 真假未定。
（4）同样的，图十二中亦可看出，如O 真，E 的真假未定，I的真假亦未定，如O（或I）假，则A（或E）真，故I（或O）亦真。
总之，传统形式逻辑正方形的从A、E、I、O 四判断中任何一种的真或假所得关于其他三种判断的推断，都可由图中直接看出。
以上是直言主谓判断的图解。以下再简单地说一下选言判断和复合判断的图解。
S是P1 或P2 这一选言判断用图十三表示如下：
图十三
图十三中1部分划掉，则S所余的是2、3、4之和。这三部分之和是存在的，但＊可能在2、3、4三部分中之任何之一部分，而不失圆的意义。如＊在2，则“S是P1”而又“S是P2”；如＊在4，则“S是P2”而又“S不是P1”；如＊在3，则“S是P1”而不是“S是P2”；所以图十三是表示一个相容的“或”。
如“或”是不相容义，则需用图十四：
图十四
在图十四中所划掉的是1与3两部分，所余的是2与4，其中应有＊以表示其存在，如＊在2则“S是P1”而不是“S是P2”；如＊在4则“S是P2”而不是“S是P1”。
S同时是P1，而又是P2，这是复合判断，用图表示如下：（见图十五）
图十五
图十五中1、2、4 部分都划掉，S 只剩下3 部分，故当以＊表示其存在，而3部分是P1 与P2 所共同的，故S是P1 同时S又是P2。
有关韦卓民全集（第9卷）的文章
- 详细阅读
-
欧拉公式适用的范围及限制条件详细阅读
欧拉公式的适用范围。欧拉公式是根据曲线近似微分方程导出的，应用此微分方程时，材料必须服从胡克定律。因此，欧拉公式的适用范围应当是压杆的临界应力σcr，不超过材料的比例极限σP，即λP为压杆的临界应力达到材料的比例极限时的柔度值，即则欧拉公式的适用范围为式（9-5）表明，当压杆的柔度λ 不小于λP 时，才可以应用欧拉公式计算临界力或临界应力。这类压杆称为大柔度杆或细长杆，欧拉公式只适用于较细长的大柔度杆。......
2023-06-19
-
数值算法对比与应用：欧拉、拉格朗日与SPH详细阅读
图2.3朗格朗日网格与欧拉网格对比欧拉算法也有其不足，体现为单个循环计算时间长、材料边界不清晰、网格区域过大、冲击波耗散大、强度模拟不精确等。图2.4欧拉-拉格朗日耦合算法模型4.SPH算法SPH算法，即光滑粒子流体动力学数值算法，为固体材料大变形，尤其是存在破坏、断裂等极大变形的非线性动力学行为数值模拟提供了新的手段。......
2023-06-18
-
韦卓民全集：图解判断变形详细阅读
判断变形有换质与换位两种形式，但由这两种形式亦可得其他形式，故这两种形式是主要的形式。传统形式逻辑从E型判断的变形得出下列8个判断：SeP原判断其变形过程，初级的形式逻辑教本皆言之甚详，且参考A 型判断变形自易明了，兹不赘述。传统形式逻辑说明由I型判断即SiP 之变形只能得出另外三个判断，连同原判断如下：SIP原判断其他四种变形在I型判断而言是不可能的。上面四种可写为：由此可见，判断的各式变形，皆可由图直接解释。......
2023-11-08
-
高等数学：欧拉方程的求解方法详细阅读
变系数的线性微分方程，一般说来都是不容易求解的.但是有些特殊的变系数线性微分方程，则可以通过变量代换化为常系数线性微分方程，因而容易求解，欧拉方程就是其中的一种.形如的方程（其中，p1，p2…pn为常数），叫做欧拉方程.作变换x=et或t=lnx，将自变量x换成t，有如果采用记号D表示对t求导的运算，那么上述计算结果可以写成一般地，有xky=D（D-1）…......
2023-11-22
-
动物的声音与人类的传播活动详细阅读
有的机场设立了鸟语广播台，播送鸟类的惊恐叫声，以便驱散它们，使飞机安全起飞和降落。有些动物常常以特殊的气味（信息素）来达到引诱异性、追踪目标、鉴别敌友、发出警报、标明地点、集合或分散群体等目的。海豚的超声语言是颇为复杂的，它们能交流情况，展开讨论，共商大计。人类的双手不仅能制造工具、创造财富，还能创造精神财富，进行传播活动。......
2023-07-18
-
欧拉公式适用范围-建筑力学（第3版）详细阅读
由于欧拉公式是假设材料在线弹性范围内的条件下，根据挠曲线近似微分方程导出的，而应用此微分方程时，材料必须适用胡克定律。故欧拉公式的适用范围是：临界应力σcr不超过材料的比例极限。即有若设λP为压杆的临界应力达到材料的比例极限σP时的柔度值，则故欧拉公式的适用范围为式表明，当压杆的柔度不小于λP时，才可以应用欧拉公式计算临界力或临界应力。这类压杆称为大柔度杆或细长杆，欧拉公式只适用于大柔度杆。......
2023-08-26
-
压杆柔度与临界应力的欧拉公式计算方法详细阅读
于是临界应力可写为令则上式为计算压杆临界应力的欧拉公式，式中λ称为压杆的柔度。从式（9-3）还可以看出，压杆的柔度值越大，则其临界应力越小，压杆就越容易失稳。因此，欧拉公式的适用范围应当是压杆的临界应力σcr不超过材料的比例极限σP，即有若设λP为压杆的临界应力达到材料的比例极限σP时的柔度值，则故欧拉公式的适用范围为上式表明，当压杆的柔度不小于λP时，才可以应用欧拉公式计算临界力或临界应力。......
2023-06-16
相关推荐