韦卓民全集：两种实际改造方法，直接归纳

2023-11-08 理论教育版权反馈

【摘要】：第一种是直接改造方法：这直接方法是根据原来那个式的两前提，通过换位，换质，或前提互换位置，而变成第一格以得出原来那个式的结论。上面所举的三个例子都是用直接改造的方法的。间接方法是第二种方法，这种方法是用第一格的式证明原来那个式的结论之矛盾命题是不正确的，因而证明原来的结论是正确的。今又认为原结论的SoP不对，故须承认其矛盾命题SaM 是正确的。

第一种是直接改造方法：这直接方法是根据原来那个式的两前提，通过换位，换质，或前提互换位置，而变成第一格以得出原来那个式的结论。上面所举的三个例子都是用直接改造的方法的。

间接方法是第二种方法，这种方法是用第一格的式证明原来那个式的结论之矛盾命题是不正确的，因而证明原来的结论是正确的。这方法又称为归谬法，意思是以谬论归之于论敌，是亚里斯多德常用的一种方法，例如第二格有下面这个式

如果有人认为结论SoP 之从PaM 和SoM 这两前提得出是不正确的，那他就得要承认，从这两前提应该得出与SoP 相矛盾的结论，那就是SaP。我们可以用第一格来证明这个结论是不可能的，而以其谬论归之于对方。其过程如下：

论敌是承认原式的两前提的，即PaM 和SoM。今又认为原结论的SoP不对，故须承认其矛盾命题SaM 是正确的。把这命题作为小前提而与原来的大前提PaM 相结合，其结论根据第一格的AAA 那第一个式便是SaM，但这命题却和原来的小前提SoM 相矛盾的，所以论敌是自相矛盾的，可见他之不接受原来的结论，必要产生自相矛盾的后果，所以原结论是正确的，这就是间接方法，归谬法的一个例子。

在实践中，格的改造虽然并不困难，但有时还须讲点思索的，为便于学生背诵，中世纪经院逻辑家把格的改造方法编成各种歌诀的韵文，其中最通行而流传至今的是罗马的天主教皇约翰第二十一世^[20]所编，其全文如下：

Barbara，Celarent，Darii，Ferioque，prioris；

Cesare，Camestres，Festino，Baroco，secundae；

Tertia，Darapti，Disamis，Datisi，Felapton，Bocardo，Ferison，habet；

Quarta insuper addit Bramantip，Camenes，Dimaris，Fesapo，Fresison.

这个韵文的歌诀一直到最近学习形式逻辑的人还有背诵的，但这是不必要的。我们现在尽可以根据三段论式的一般规则或其他简易的方法，如附录六的图解，来检查任何一个三段论式的正确性，必须靠格的改造这种方法，可是作为一种逻辑史的材料，我们把这韵文的用法详细说明，列为附录八，以供参考。

【注释】

[1]我们在这里说，逻辑正方形上某些对当关系，而不是说所有对当关系，可以说是直接推理形式，因为从A 之真而到I之真，显然不是推理，其不是推理，因为说A 之真时，已经知道I之真，故I之真不是从A 之真推论出来的，而是已经包含在A 之真里面的。但是当我们说O 之假，并不确知I之真，要想到何以O 是假，是因为全类，即A 是真，才知I必真，所以才说这是推理。把逻辑正方形上所有对当在系都说成是直接推理，只是记住推理从一个前提而得出“结论”这一点，而未问到是否通过推理而得出另一判断。我们要记住推理是由已知到未知的一种过程。在A 之真已经知道I之真的，故由A 之真到I之真不是一种推理过程。

[2]毛泽东：《矛盾论》，人民出版社，1956年，单行本，第14页。

[3]毛泽东：《矛盾论》，人民出版社，1956年，单行本，第14页。

[4]毛泽东：《矛盾论》，人民出版社，1956年，单行本，第14页。

[5]参看毛泽东：《矛盾论》，人民出版社，1956年，单行本，第14页。第三大段，至少从第12至16页。(www.chuimin.cn)

[6]苏联科学院哲学研究所1954年三月底出版康达科夫著的《逻辑》一书是把“归纳推理”摆在第八章，“演绎推理”摆在第九章，“类比”摆在第十章的。

[7]恩格斯：《反杜林论》，俄文版，1948年，第317页。此部分中译本未译出。

[8]当然我们不否认在谈到动植物间的关系时，也可以用“父亲”的这种关系名称，但这是转借于人与人之间的关系的。

[9]参看拙著《亚里斯多德逻辑》，科学出版社，1957年，第64—65页、67—69页。

[10]如果a真则b必真，我们便说a含蕴b。含蕴关系不同于包含关系，因为a含蕴b，同时b也可能含蕴a，其关系是可对称的，但a如果包含着b，则b不能同时包含着a，其关系是非对称的。从对称讲，一种关系可能是（1）对称的，例如“等于”，如a等于b，则b必等于a，（2）可对称的，例如“了解”，a了解b，而b可能了解或不了解a，（3）非对称，如“在上面”，如果a在b的上面，b绝不能同时也在a的上面，含蕴关系属于（2）类。

[11]波兰著名的数理逻辑家卢卡西维茨（Jan Lukasiewicz）在其1951年在爱尔兰以英文出版的《亚里斯多德的三段论式学》一书中认为我们通常使有的三段论式形式不是亚里斯多德原来所用的，不是“凡人皆有死，苏格拉底是人，所以，苏格拉底必有死”，因亚里斯多德的三段论式系统中并无单称名词或单称前提的使用，即“凡人皆有死，凡希腊人都是人，所以，凡希腊人皆有死”，虽比较近于亚氏的三段论式形式，然而毕竟不是他原来所用的。他原来所用的形式不是一种推理形式而是一种含蕴的形式，“是以前提的结合为其前项而以其结论为后项的含蕴形式”（该书英文原版第2页）。所以亚氏三段论式的其正例子应该是下面的样式的：“如果所有人皆有死，而所有希腊人都是人，那么，所有希腊人皆有死。”（见该书同上页）参看《教学与研究》杂志1957年第12期黄顺基著《介绍卢卡西维茨的〈亚里斯多德的三段论〉》一文。

[12]按亚里斯多德所用的“中词”，其希腊文为με＇σον，原有“共同地域”这一意思，后世译为拉丁文terminus medius，其形容词medius亦有媒介义。

[13]这公理严复译为“曲全公理”，见严译《穆勒名学》（2）第18、19页。其拉丁文一种条文是：Quidquid dictur universum de aliquo subiecto，affirmatur de quovis contento sub illo，quidquid negatur de aliquo universaliter accepto negateer de omnibus de quibus illud alterum affermatur.另一种条文是今日之称为遍有遍无公理所根据。其全文如下：Quidquid de omni valet，valet etiam de quibusdam et de singulis.Quidquid de nullo valet，nec de quibusdam valet，nec de singulis.中文直译是：“凡可以之肯定或否定全类的亦可以之而肯定或否定其类之任何一部分或任何一事物。”这公理简称为dictum de omni et nulls，其标题的de oumnoe at vuolla直译是“关于全类和关于没有一个”，故译为“遍有遍无”，似乎比严译的“曲全”为通俗，这是条文的严译是“凡于一类之全而有所谓者，于其曲有所不谓也”，故其曲全公理的“曲全”是译条文的内容，而不是译de oumnoe at vuolla的标题，这条文也只是从曲全的外延来讲的，故曲全类而列其任何一事物，另一种条文是从曲全的内涵来讲的，其全文如下Nota notae est nota rei ipsius.Repugnans notae，repugnant rei ipsi.中文译为“凡事物属性的属性，也就是事物自身的属性。凡与事物属性矛盾的，也是与事物自身矛盾”。

[14]参看卢卡西维茨：《亚里斯多德的三段论》一书，1951年，英文原版，第73页。据卢氏的研究，“遍有遍无公理原非出自亚里斯多德作为一切三段论式推理的根据，如凯因斯所断言那样。亚氏在其《分析论前篇》并没有在什么地方把这公理作成公式表达为三段论式的原理。有时人们引用为这原理的公式表示的也不过是‘用以对所有陈述’和‘不对任何一个东西陈述’这两种说法的解释而已”（译自上引书第47页）。这种看法，严格地说来，是正确的，在亚里斯多德现存的著作中，确无遍有遍无公理的条文，但有两段文字是和其内容有关的。其第一段见《分析论前篇》，标准页第24b第26至30行，其中一部分也是卢氏在上引文中所引用的。其整段全文中译如下：“一个词全部包含在另一个词之内，就是等于以第2个词来称谓第1个词之全部。所谓以一个词来称谓另一个词的全部，就是说，没有主词所指的任何事例是谓词所不能称谓的。不能以一个词来称谓另一个词的任何部分，其结果也可以由此类推。”另一地方是《范畴篇》标准页第1b，第10至16行。中译如下：“如果以某一东西来称谓另一东西，则凡可以之称谓其谓词者，亦可以之称谓其主词。”例如，以“人”来称谓某甲，而又可以“动物”来称谓“人”，因之亦可以“动物”来称谓某甲，即可以说，某甲是“人”而同时又是“动物”。这两段文字的第一段就是遍有遍无公理从概念外延看的内容，其第二段就是公理从内涵看的内容。但是公理的条文是以拉丁文写出，据普兰特尔的《西方逻辑史》第一卷，原德文版，第652页又第649页，是波亚提奥斯在公元5、6世纪之际才确定是从亚里斯多德而来的。参看拙著《亚里斯多德》，第119—120页。

[15]原来亚里斯多德只认为我们现在的前三个格，其第四格是后人增加上去的。何以亚里斯多德只承认三个格呢？他曾说过，“由中词的位置而知其格”（《分析论前篇》标准页第47b，第14行）。按我们现在那样来分别中词在两前提的位置，显然就有四个格，缺一不可。但是亚里斯多德在谈到三段论式中词在前提的位置时，是这样说的：“如果中词在两肯定前提中，一为主词，一为宾词，或者它是一个前提的宾词，而又为一否定前提的主词，那就是第一格；如果中词是一肯定前提的宾词而同时又是否定前提的宾词那就是中间格；如果中词是两肯定前提的主词，或者是一肯定前提的主词，另一否定前提的主词，那就是最后一格。”（同上标准页第1至13行）从这段引文可以看出，亚里斯多德没有像我们现在那样把大前提和小前提分别开来看，中词是大前提的主词抑或是小前提的主词，而只说为主词，一为宾词……这样就可把现在的第一和第四格摆放在一起而不分开，所以他只有三个格，同时，我们须知道亚里斯多德的格的划分有他的划分根据，不同于我们只有中词在前提所说的位置是主词或宾词的，他是根据中词和大小词的宽度的比较的。如果我们以这为划分格的根据而将亚氏的三个格列为公式，则有下面的情况：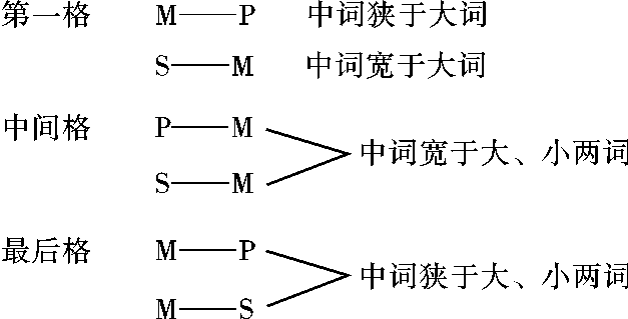
pagenumber_ebook=366,pagenumber_book=350
这样一来，是不能分出第四个格来的。所以亚里斯多德只有三个格。
原来的第一格是可以包括今日的第一格和第四格的。参看拙著《亚里斯多德逻辑》，科学出版社，1957年，第181—183页。现在一般都认为第四格是公元2世纪格伦所提出，故称为格伦格，据英国逻辑家凯因斯的考证，以第四格为格伦所提出，是公元12世纪西班牙系的亚拉伯人，亚里斯多德的权威注释家阿弗罗厄斯（Averroёs）的意见。第四格之称为“格伦格”从此始。在18世纪初叶之前，形式逻辑各典籍中没有第四格的出现，即近代逻辑家亦多不主张列入第四格而保持亚氏的传统的，约瑟在其《逻辑导论》一书便是一例，他认为加入第四格是一种错误，参看该书原英文第二版第262页（全书有拙译，尚未出版）。当然还有其他逻辑家持不同的意见，例如英国近代另一逻辑家庄逊便写道：“对于第四格之列为逻辑三段论式的一格，成见很深，而且这成见由来很久，主张不以之列入的意见，大都是这样论证的：‘凡值得列为逻辑推理形式的都是平常议论中所运用的，今察得，没有什么在平常议论中所运用的是第四格，所以，第四格不是值得列为逻辑推理形式的。’庄逊就反驳说：‘这论证就已是第四格的形式，基谬可不置辩。’”参看凯因斯（J.N.Keynes）：《形式逻辑》英文原版，第326—329 页。上文是据P.M.Eaton 在其《逻辑概要》（General logic）1931年英文原版第112页所引。可是，波兰逻辑家卢卡西维茨在其1951年出版的《亚里斯多德的三段论》一书里认为“把第四格作为格伦的创作是一种长期的错误”，他指出格伦所研究的是含有四个名词的复合三段论式而把这种复合三段论式划分为四个格，并非我们所知道带有中世纪名称的这些简单的三段论式。参看该书英文原版第38—41页、又第74—75页。

[16]这种方法详见本书附录七——检查三段论式的式之一种方法，可参考。

[17]参看拙著《亚里斯多德逻辑》，科学出版社，1957年，第120—123页。

[18]亚里斯多德：《分析论前篇》，标准页第43a第23至26行。

[19]亚里斯多德的三段论式没有第四格。

[20]教皇约翰二十一世Pedro Hispano，卒于1277年。

韦卓民全集：两种实际改造方法，直接归纳

相关推荐